ML Aggarwal Class 6 Solutions Chapter 4 Playing with Numbers Ex 4.5 for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5

Question 1.
Find the L.C.M. of the given numbers by prime factorisation method :
(i) 28, 98
(ii) 36, 40, 126
(iii) 108, 135, 162
(iv) 24, 28, 196.
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 1
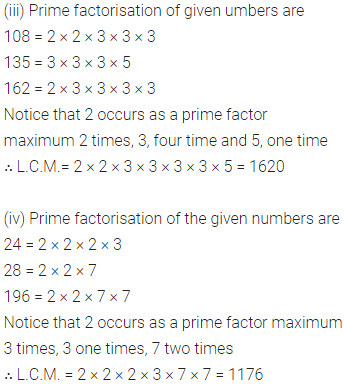
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 2

Question 2.
Find the L.C.M. of the given numbers by division method :
(i) 480, 672
(ii) 6, 8, 45
(iii) 24, 40, 84
(iv) 20, 36, 63, 67
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 3
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 4

Question 3.
Find the least number which when increased by 15 is exactly divisible by 15, 35 and 48.
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 5

Question 4.
Find the least number which when divided by 6, 15 and 18 leaves remainder 5 in each case.
Solution:
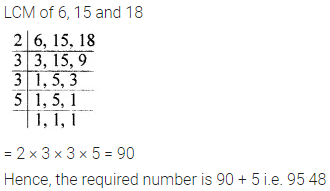
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 6

Question 5.
Find the least number which when divided by 24, 36, 45 and 54 leaves a remainder of 3 in each case.
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 7

Question 6.
Find the greatest 3-digit number which is exactly divisible by 8, 20 and 24.
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 8

Question 7.
Find the smallest 4-digit number which is exactly divisible by 32, 36 and 48.
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 9
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 10

Question 8.
Find the greatest 4-digit number which is exactly divisible by each of 8, 12 and 20.
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 11
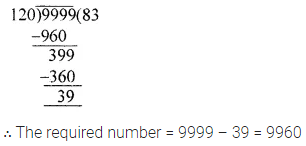
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 12

Question 9.
Find the least number of five digits which is exactly divisible by 32, 36 and 45.
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 13
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 14

Question 10.
Three boys step off together from the same spot. Their steps measure 63 cm, 70 cm and 77 cm respectively. What is the minimum distance each should cover so that all can cover the same distance in complete steps?
Solution:
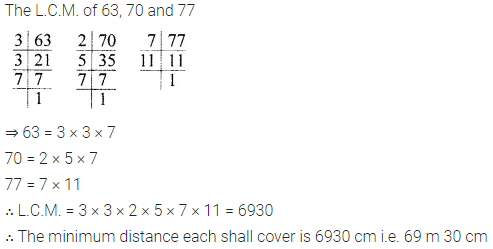
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 15

Question 11.
Traffic lights at three different road crossing change after 48 seconds, 72 seconds and 108 seconds respectively. At what time will they change together again if they change simultaneously at 7 A.M.?
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 16

Question 12.
If the product of two numbers is 4032 and their HCF is 12, find their LCM.
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 17

Question 13.
The HCF and LCM of two numbers are 9 and 270 respectively. If one of the numbers is 45, find the other number.
Solution:
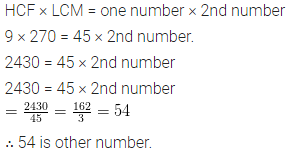
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 18

Question 14.
Find the HCF of 180 and 336. Hence, find their LCM.
Solution:
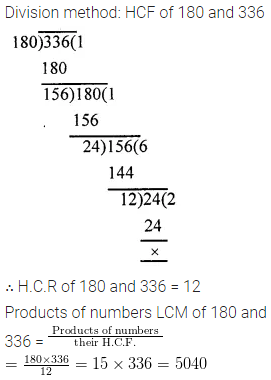
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 19

Question 15.
Can two numbers have 15 as their HCF and 110 as their LCM? Give reason to justify your answer.
Solution:
ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5 20