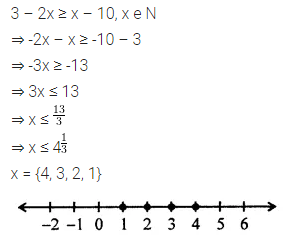ML Aggarwal Class 7 ICSE Maths Model Question Paper 3

ML Aggarwal Class 7 Solutions for ICSE Maths Model Question Paper 3 acts as the best resource during your learning and helps you score well in your exams.

ML Aggarwal Class 7 ICSE Maths Model Question Paper 3

(Based on Chapters 1 to 9)
Time allowed: 2\(\frac { 1 }{ 2 }\) Hours
Maximum Marks: 90

General Instructions

• All questions are compulsory.
• The question paper consists of 29 questions divided into four sections A, B, C and D.
• Section A comprises of 8 questions of 1 mark each.
• Section B comprises of 6 questions of 2 marks each.
• Section C comprises of 10 questions of 4 marks each and
• Section D comprises of 5 questions of 6 marks each.
• Question numbers 1 to 8 in Section A is multiple choice questions where you are to select one correct option out of the given four.

Section – A

Question numbers 1 to 8 are of 1 mark each.
Question 1.
The number of integers between -16 and 5 is
(a) 19
(b) 20
(c) 21
(d) 22
Solution:

Question 2.
50 m 5 cm is the same as
(a) 50.5 m
(b) 50.05 m
(c) 50.005 m
(d) 5.05 m
Solution:

Question 3.

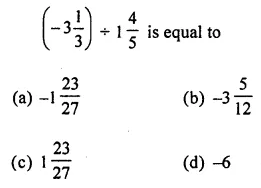
Solution:

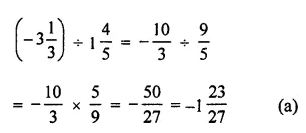
Question 4.
The number 5,540,000,000,000 in the scientific notation can be written as:
(a) 554 × 10¹⁰
(b) 55.4 × 10¹¹
(c) 5.54 × 10¹²
(d) 5.54 × 10¹¹
Solution:

Question 5.
The number of unlike terms in the expression 5x²y – 2xy² – 2yx² + 3y(xy + y²) + 7 is
(a) 3
(b) 4
(c) 5
(d) 6
Solution:

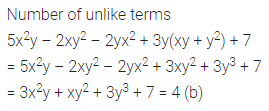
Question 6.
x = -2 is a solution of the equation
(a) 2x + 5 = 9
(b) 3x – 1 = 5
(c) 4x + 3 = 1
(d) 5x + 12 = 2
Solution:

Question 7.
The ratio of the number of girls to the number of boys in a class is 5 : 4. If there are 16 boys in the class, then the number of students in the class is
(a) 20
(b) 32
(c) 36
(d) 45
Solution:

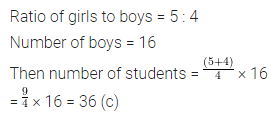
Question 8.
If 12% of a number is 9, then the number is
(a) 36
(b) 48
(c) 60
(d) 75
Solution:

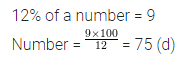
Section – B

Question numbers 9 to 14 are of 2 marks each.
Question 9.
Using suitable properties, evaluate:
238 × (-44) + (-238) × 56.
Solution:

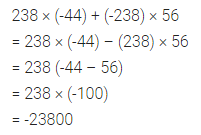
Question 10.
State whether each of the following statement is true or false for the sets P and Q where P = {letters of TITLE} and Q = {letters of LITTLE}
(i) P ↔ Q
(ii) P = Q
Solution:

Question 11.
Evaluate: -3\(\frac { 3 }{ 8 }\) – (-2\(\frac { 1 }{ 6 }\))
Solution:

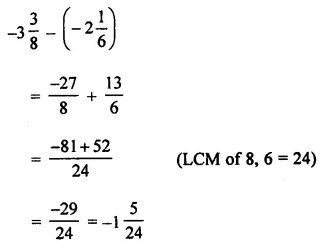
Question 12.
Simplify and express in the exponential form: (4³ × 3⁶) ÷ (16 × 9²).
Solution:

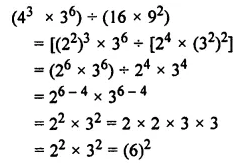
Question 13.
If I earn ₹ 75000 per month and spend ₹ 40000 per year for helping poor students then find the ratio of the money spent on helping poor students and the annual income.
Solution:

Question 14.
If ₹ 4000 amounts to ₹ 5000 in 2 years, find the rate of simple interest per annum.
Solution:

Section – C

Question numbers 15 to 24 are of 4 marks each.
Question 15.
Simplify:

Solution:

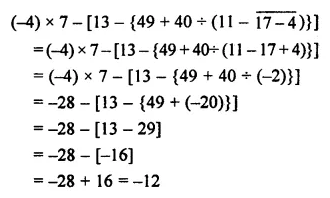
Question 16.
Vikram’s monthly salary is ₹ 12750. He spends \(\frac { 1 }{ 5 }\) of his salary on food and out of the remaining, he spends \(\frac { 1 }{ 4 }\) on rent and \(\frac { 1 }{ 6 }\) on the education of children. Find
(i) how much he spends on each item?
(ii) how much money is still left with him?
Solution:

Question 17.
Insert five rational numbers between \(\frac { -2 }{ 5 }\) and \(\frac { -1 }{ 3 }\)
Solution:

Question 18.
Afzal can walks 5\(\frac { 3 }{ 4 }\) km in one hour. How much distance will he cover in 2 hours 40 minutes? What are the health advantages of having a brisk walk?
Solution:

Question 19.
If a vehicle covers a distance of 57.72 km in 3.7 litres of petrol. How much distance will it cover in one litre of petrol?
Solution:

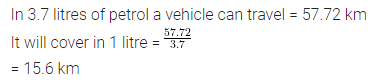
Question 20.
The perimeter of a triangle is 5 – 3x + 7x² and two of its sides are 2x² + 3x – 2 and 3x² – x + 3. Find the third side of the triangle.
Solution:

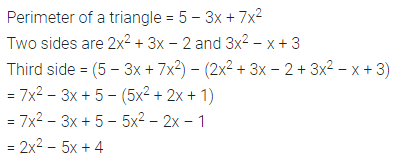
Question 21.

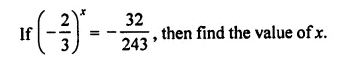
Solution:

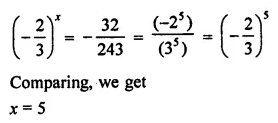
Question 22.
Solve the equation: 3(2x – 1) – 2(2 – 5x) = 1
Solution:

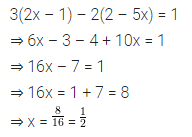
Question 23.
If 74% of the population of a village is illiterate and the number of literate people is 2158, then find the population of the village.
Solution:

Question 24.
Simplify:

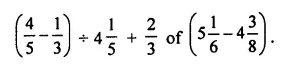
Solution:

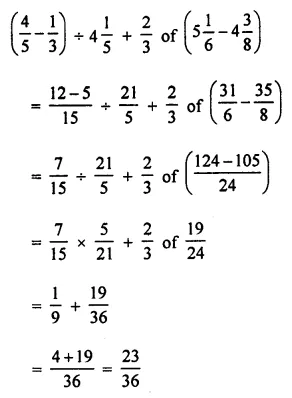
Section – D

Question numbers 25 to 29 are of 6 marks each.
Question 25.
If we represent the distance above the ground by a positive rational number and that below the ground by a negative rational number, then answer the following question:
An elevator descends into a mine shaft at the rate of 4\(\frac { 3 }{ 4 }\) metre per minute. If it begins to descend from 7\(\frac { 1 }{ 2 }\) metre above the ground, what will be its position after 18 minutes from the ground?
Solution:

Question 26.
In a competition, the question paper consists of 25 questions. 4 marks are awarded for every correct answer, 2 marks are deducted for every incorrect answer and no marks for not attempting a question. If Vaishali scored 58 marks and got 17 correct answers, how many questions she attempted incorrectly? How many questions she did not attempt?
Solution:

Question 27.
Divide ₹ 216000 into two parts such that one-fourth of one part is equal to one-fifth of the other part. Find the two parts.
Solution:

Question 28.
If a table is sold for ₹ 437 at a loss of 8%, find its cost price. At what price must it be sold to gain 10%?
Solution:

Question 29.
Solve the inequality:
3 – 2x ≥ x – 10, x ∈ N.
Also, represent its solution set on the number line.
Solution: