ML Aggarwal Class 7 Solutions Chapter 12 Congruence of Triangles Objective Type Questions for ICSE Understanding Mathematics acts as the best resource during your learning and helps you score well in your exams.
ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 12 Congruence of Triangles Objective Type Questions
Mental Maths
Question 1.
Fill in the blanks:
(i) Two line segments are congruent if ……….
(ii) Among two congruent angles, one has a measure of 63°; the measure of the other angle is ……….
(iii) When we write ∠A = ∠B, we actually mean ………
(iv) The side included between ∠M and ∠N of ∆MNP is ……….
(v) The side QR of ∆PQR is included between angles ……….
(vi) If two triangles ABC and PQR are congruent under the correspondence A ↔ R, B ↔ P and C ↔ Q, then in symbolic form it can be written as ∆ABC = ………
(vii) If ∆DEF = ∆SRT, then the correspondence between vertices is ……….
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) All circles are congruent.
(ii) Circles having equal radii are congruent.
(iii) Two congruent triangles have equal areas and equal perimeters.
(iv) Two triangles having equal areas are congruent.
(v) Two squares having equal areas are congruent.
(vi) Two rectangles having equal areas are congruent.
(vii) All acute angles are congruent.
(vii)All right angles are congruent.
(ix) Two figures are congruent if they have the same shape.
(x) A two rupee coin is congruent to a five rupee coin.
(xi) All equilateral triangles are congruent.
(xii) Two equilateral triangles having equal perimeters are congruent.
(xii) If two legs of one right triangle are equal to two legs of another right angle triangle, then the two triangles are congruent by SAS rule.
(xiv) If three angles of two triangles are equal, then triangles are congruent.
(xv) If two sides and one angle of one triangle are equal to two sides and one angle of another triangle, then the triangle are congruent.
Solution:


Multiple Choice Questions
Choose the correct answer from the given four options (3 to 14):
Question 3.
Which one of the following is not a standard criterion of congruency of two triangles?
(a) SSS
(b) SSA
(c) SAS
(d) ASA
Solution:

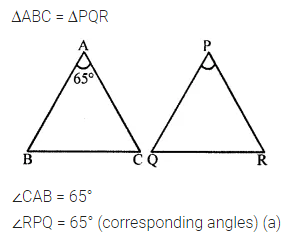
Question 4.
If ∆ABC = ∆PQR and ∠CAB = 65°, then ∠RPQ is
(a) 65°
(b) 75°
(c) 90°
(d) 115°
Solution:
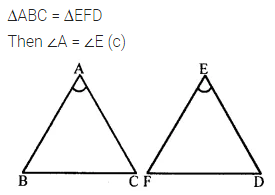
Question 5.
If ∆ABC = ∆EFD, then the correct statement is
(a) ∠A = ∠D
(b) ∠A = ∠F
(c) ∠A = ∠E
(d) ∠B = ∠E
Solution:
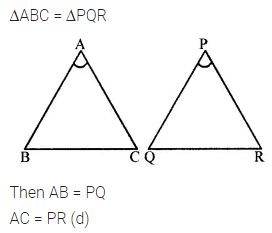
Question 6.
If ∆ABC = ∆PQR, then the correct statement is
(a) AB = QR
(b) AB = PR
(c) BC = PR
(d) AC = PR
Solution:
Question 7.
If ∠D = ∠P, ∠E = ∠Q and DE = PQ, then ∆DEF = ∆PQR, by the congruence rule
(a) SAS
(b) ASA
(c) SSS
(d) RHS
Solution:

Question 8.
In ∆ABC and ∆PQR, BC = QR and ∠C = ∠R. To establish ∆ABC = ∆PQR by SAS congruence rule, the additional information required is
(a) AC = PR
(b) AB = PR
(c) CA = PQ
(d) AB = PQ
Solution:

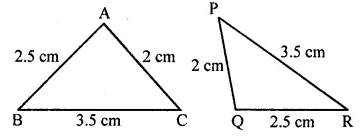
Question 9.
In the given figure, the lengths of the sides of two triangles are given. The correct statement is
(a) ∆ABC = ∆PQR
(b) ∆ABC = ∆QRP
(c) ∆ABC = ∆QPR
(d) ∆ABC = ∆RPQ
Solution:
![]()
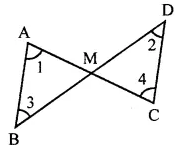
Question 10.
In the given figure, M is the mid-point of both AC and BD. Then
(a) ∠1 = ∠2
(b) ∠1 = ∠4
(c) ∠2 = ∠4
(d) ∠1 = ∠3
Solution:

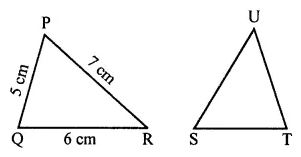
Question 11.
In the given figure, ∆PQR = ∆STU. What is the length of TU?
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) cannot be determined
Solution:

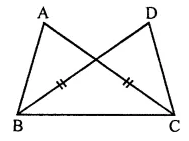
Question 12.
In the given figure, ∆ABC and ∆DBC are on the same base BC. If AB = DC and AC = DB, then which of the following statement is correct?
(a) ∆ABC = ∆DBC
(b) ∆ABC = ∆CBD
(c) ∆ABC = ∆DCB
(d) ∆ABC = ∆BCD
Solution:

Question 13.
The two triangles shown in the given figure are:
(a) congruent by AAS rule
(b) congruent by ASA rule
(c) congruent by SAS rule
(d) not congruent.
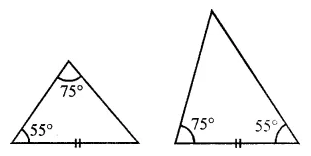
Solution:

Question 14.
In .the given figure, ∆ABC = ∆PQR. The values of x and y are:
(a) x = 63, y = 35
(b) x = 77, y = 35
(c) x = 35, y = 77
(d) x = 63, y = 40
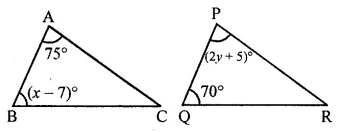
Solution:
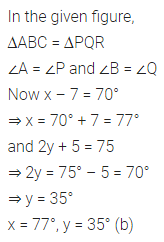
Higher Order Thinking Skills (HOTS)
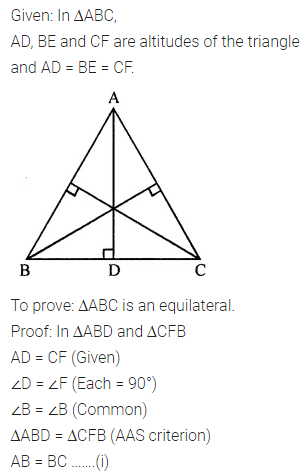
Question 1.
If all the three altitudes of a triangle are equal, then prove that it is an equilateral triangle.
Solution:

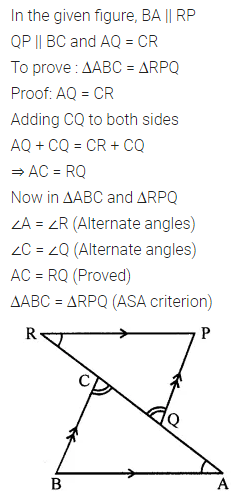
Question 2.
In the given fig., if BA || RP, QP || BC and AQ = CR, then prove that ∆ABC = ∆RPQ.
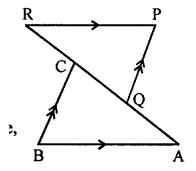
Solution: