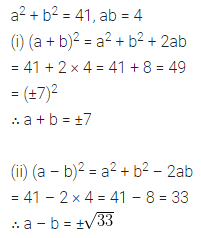ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 10 Algebraic Expressions and Identities Ex 10.5

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 10 Algebraic Expressions and Identities Ex 10.5

Question 1.
Using suitable identities, find the following products:
(i) (3x + 5) (3x + 5)
(ii) (9y – 5) (9y-5)
(iii) (4x + 11y) (4x – 11y)
(iv) \(\left(\frac{3}{2} m+\frac{2}{3} n\right)\left(\frac{3}{2} m-\frac{2}{3} n\right)\)
(v) \(\left(\frac{2}{a}+\frac{5}{b}\right)\left(\frac{2}{a}+\frac{5}{b}\right)\)
(vi) \(\left(\frac{p^{2}}{2}+\frac{2}{q^{2}}\right)\left(\frac{p^{2}}{2}-\frac{2}{q^{2}}\right)\)
Solution:

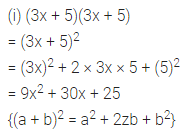
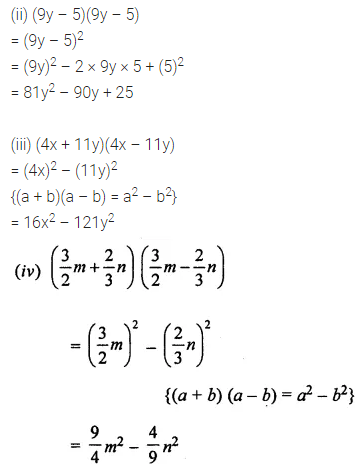
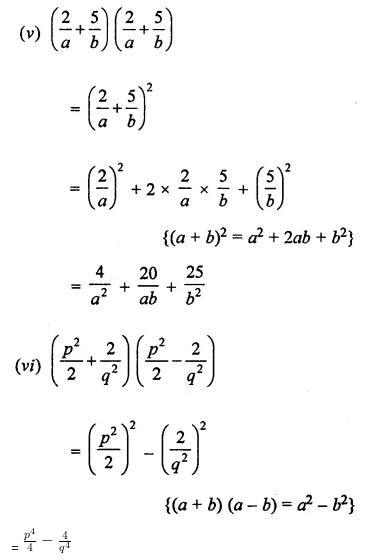
Question 2.
Using the identities, evaluate the following:
(i) 81²
(ii) 97²
(iii) 105²
(iv) 997²
(v) 6.1²
(vi) 496 × 504
(vii) 20.5 × 19.5
(viii) 9.62
Solution:

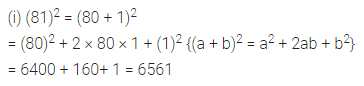
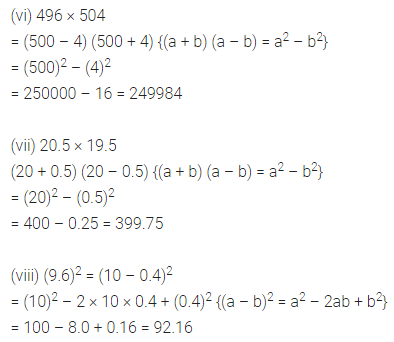
Question 3.
Find the following squares, using the identities:

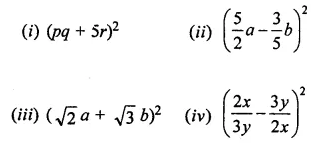
Solution:

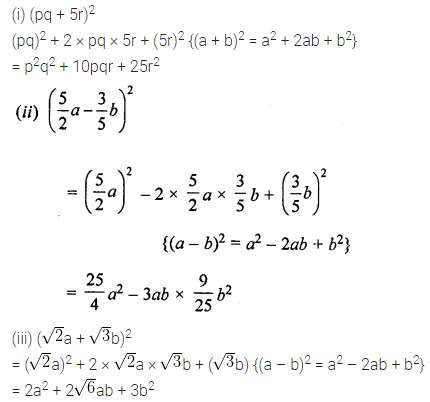
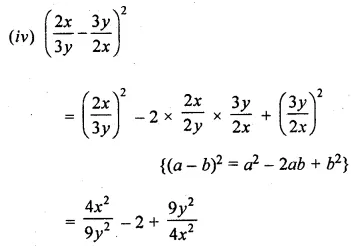
Question 4.
Using the identity, (x + a) (x + b) = x² + (a + b)x + ab, find the following products:
(i) (x + 7) (x + 3)
(ii) (3x + 4) (3x – 5)
(iii) (p² + 2q) (p² – 3q)
(iv) (abc + 3) (abc – 5)
Solution:

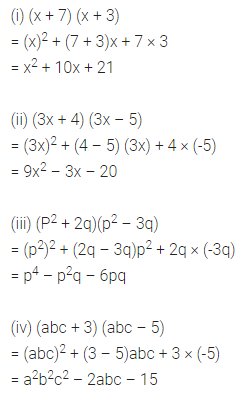
Question 5.
Using the identity, (x + a) (x + b) = x² + (a + b)x + ab, evaluate the following:
(i) 203 × 204
(ii) 8.2 × 8.7
(iii) 107 × 93
Solution:

Question 6.
Using the identity a² – b² = (a + b) (a – b), find
(i) 53² – 47²
(ii) (2.05)² – (0.95)²
(iii) (14.3)² – (5.7)²
Solution:

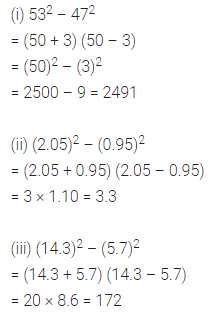
Question 7.
Simplify the following:
(i) (2x + 5y)² + (2x – 5y)²
(ii) \(\left(\frac{7}{2} a-\frac{5}{2} b\right)^{2}-\left(\frac{5}{2} a-\frac{7}{2} b\right)^{2}\)
(iii) (p² – q²r)² + 2p²q²r
Solution:

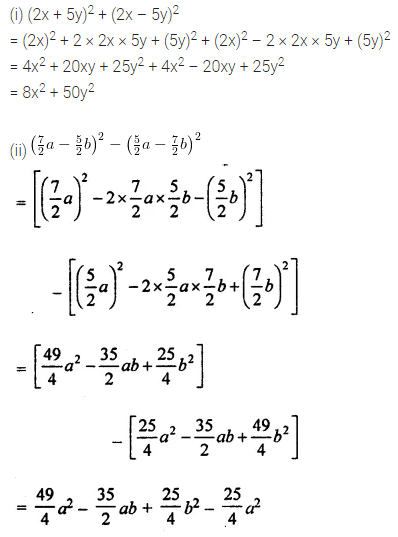
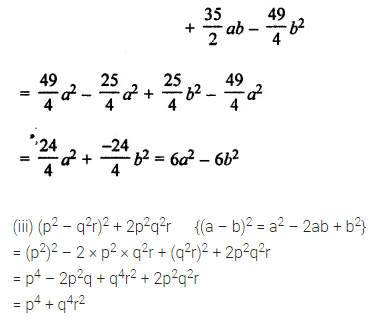
Question 8.
Show that:
(i) (4x + 7y)² – (4x – 7y)² = 112xy
(ii) \(\left(\frac{3}{7} p-\frac{7}{6} q\right)^{2}+p q=\frac{9}{49} p^{2}+\frac{49}{36} q^{2}\)
(iii) (p – q)(p + q) + (q – r)(q + r) + (r – p) (r + p) = 0
Solution:

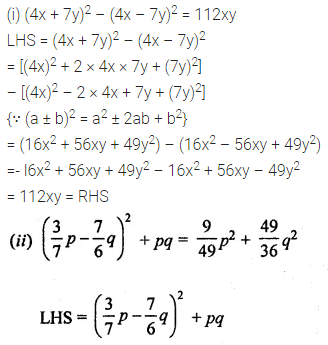
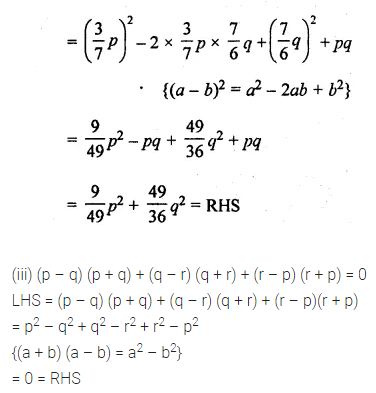
Question 9.
If x + \(\frac{1}{x}\) = 2, evaluate:

Solution:

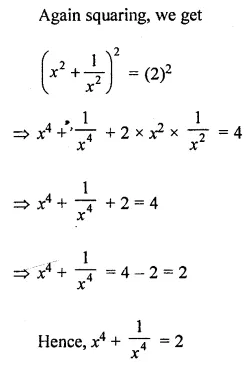
Question 10.
If x = \(\frac{1}{x}\) = 7, ecaluate:

Solution:

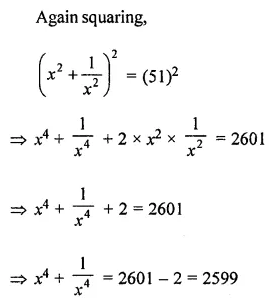
Question 11.
If x² + \(\frac{1}{x^{2}}\) = 23, evaluate:

Solution:

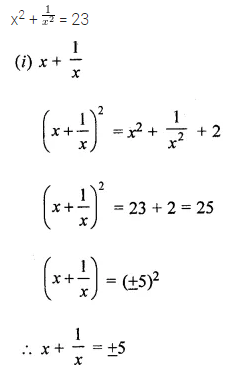
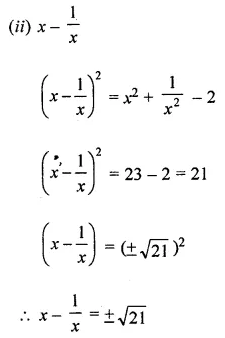
Question 12.
If a + b = 9 and = 10, find the value of a² + b².
Solution:

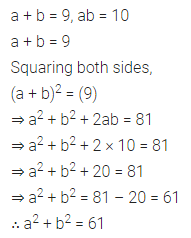
Question 13.
If a – b = 6 and a² + b² = 42, find the value of
Solution:

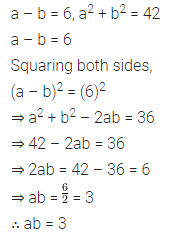
Question 14.
If a² + b² = 41 and ab = 4, find the values of
(i) a + b
(ii) a – b
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths