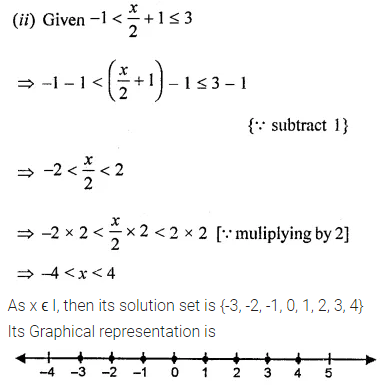ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 12 Linear Equations and Inequalities in One Variable Ex 12.3
Question 1.
If the replacement set = {-7, -5, -3, – 1, 3}, find the solution set of:
(i) x > – 2
(ii) x < – 2
(iii) x > 2
(iv) -5 < x ≤ 5
(v) -8 < x < 1
(vi) 0 ≤ x ≤ 4
Solution:

Question 2.
Represent the solution of the following inequalities graphically:
(i) x ≤ 4, x ϵ N
(ii) x < 5, x ϵ W
(iii) -3 ≤ x < 3, x ϵ I
Solution:

Question 3.
If the replacement set is {-6, -4, -2, 0, 2, 4, 6}, then represent the solution set of the inequality – 4 ≤ x < 4 grahically.
Solution:
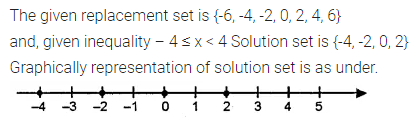
Question 4.
Find the solution set of the inequality x < 4 if the replacement set is
(i) {1, 2, 3, ………..,10}
(ii) {-1, 0, 1, 2, 5, 8}
(iii) {-5, 10}
(iv) {5, 6, 7, 8, 9, 10}
Solution:

Question 5.
If the replacement set = {-6, -3, 0, 3, 6, 9, 12}, find the truth set of the following.:
(i) 2x – 3 > 7
(ii) 3x + 8 ≤ 2
(iii) -3 < 1 – 2x
Solution:
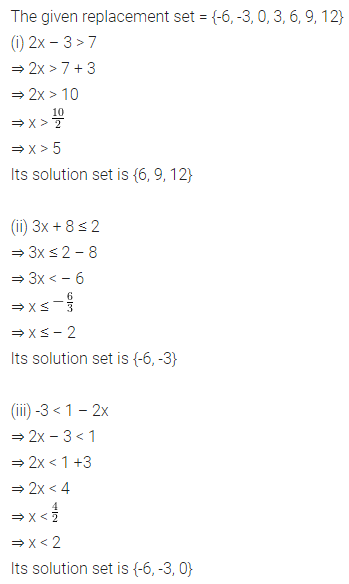
Question 6.
Solve the following inequations:
(i) 4x + 1 < 17, x ϵ N
(ii) 4x + 1 ≤ 17, x ϵ W
(iii) 4 > 3x – 11, x ϵ N
(iv) -17 ≤ 9x – 8, x 6ϵ Z
Solution:
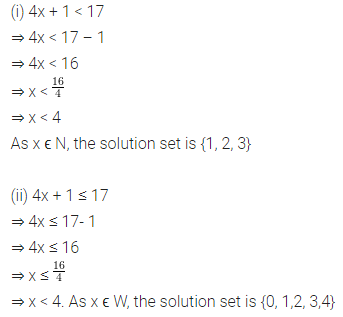
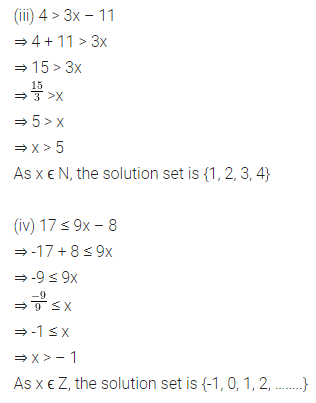
Question 7.
Solve the following inequations :
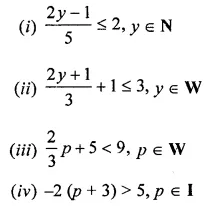
Solution:
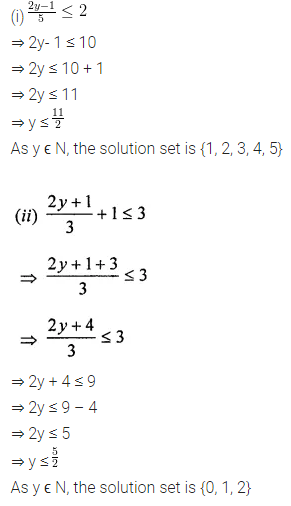
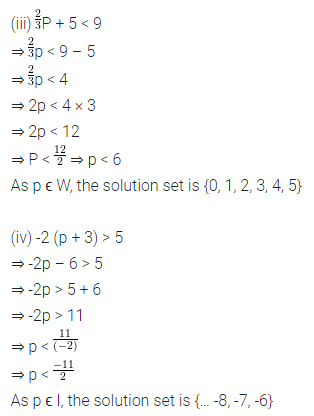
Question 8.
Solve the following inequations:
(i) 2x – 3 < x + 2, x ϵ N
(ii) 3 – x ≤ 5 – 3x, x ϵ W
(iii) 3 (x – 2) < 2 (x -1), x ϵ W
(iv) \(\frac{3}{2}-\frac{x}{2}\) > -1, x ϵ N
Solution:
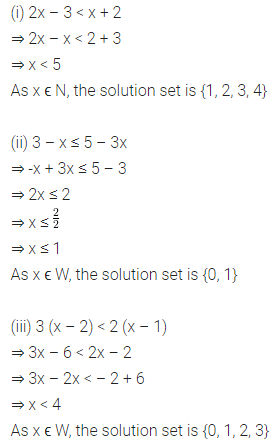
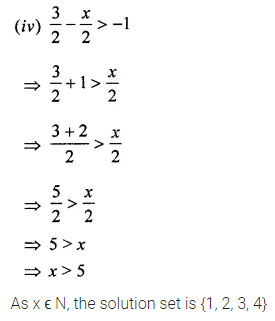
Question 9.
If the replacement set is {-3, -2, -1,0, 1, 2, 3} , solve the inequation \(\frac{3 x-1}{2}<2\). represent its solution on the number line.
Solution:

Question 10.
Solve \(\frac{x}{3}+\frac{1}{4}<\frac{x}{6}+\frac{1}{2}\), x ϵ W. Also represent its solution on the number line.
Solution:
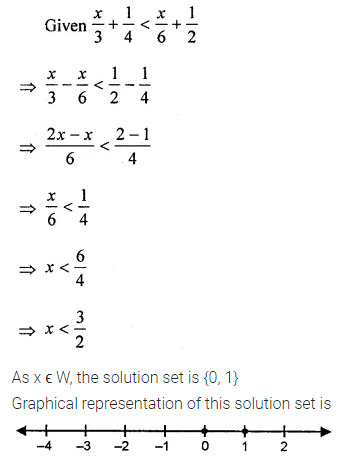
Question 11.
Solve the following inequations and graph their solutions on a number line
(i) -4 ≤ 4x < 14, x ϵ N
(ii) -1 < \(\frac{x}{2}\) + 1 ≤ 3, x ϵ I
Solution: