ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 12 Linear Equations and Inequalities in one Variable Objective Type Questions
Mental Maths
Question 1.
Fill in the blanks:
(i) An equation of the type ax + b = 0 where a ≠ 0 is called a …………. in variable x.
(ii) Any value of the variable which satisfies the equation is called a …………. of the equation.
(iii) The process of finding all the solutions of an equation is called ………….
(iv) We can add the …………. to both sides of an equation.
(v) We can divide both sides of an equation by the same …………. number.
(vi) The solution set of the inequality 3x ≤ 10, x ϵ N is ………….
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) An equation is a statement that two expressions are equal.
(ii) A term may be transposed from-one side of the equation to the other side, but its sign will not change.
(iii) We cannot subtract the same number from both sides of an equation.
(iv) 3x + 2 = 4(x + 7) + 9 is a linear equation in variable x.
(v) x = 1 is the solution of equation 4(x + 5) = 24.
Solution:

Multiple Choice Questions
Choose the correct answer from the given four options (3 to 16):
Question 3.
Which of the following is not a linear equation in one variable?
(a) 3x + 2 = 0
(b) 2y – 4 = y
(c) x + 2y = 7
(d) 2(x – 3) + 7 = 0
Solution:
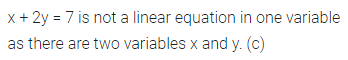
Question 4.
The solution of the equation \(\frac{2}{3} x+1=\frac{15}{9}\) is
(a) 1
(b) \(\frac{3}{2}\)
(c) 2
(d) \(\frac{2}{3}\)
Solution:
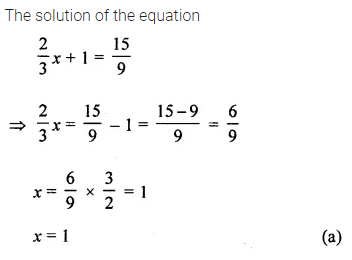
Question 5.
The solution of the equation 4z + 3 = 6 + 2z is
(a) 1
(b) \(\frac{3}{2}\)
(c) 2
(d) 3
Solution:
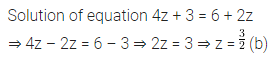
Question 6.
The solution of the equation \(\frac{3 x}{5}+1=\frac{4 x}{15}\) is +7 is
(a) 12
(b) 14
(c) 16
(d) 18
Solution:
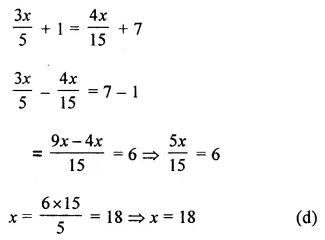
Question 7.
The solution of the equation \(\frac{x}{2}-\frac{1}{5}=\frac{x}{3}+\)\(\frac{1}{4}\) is
(a) 2.7
(b) 1.8
(c) 2.9
(d) 1.7
Solution:
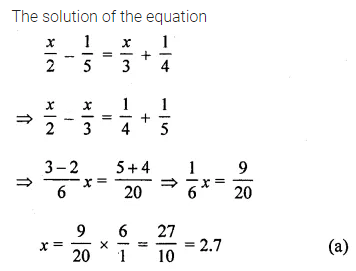
Question 8.
The solution of the equation \(\frac{8 x-3}{3 x}=2\) is

Solution:
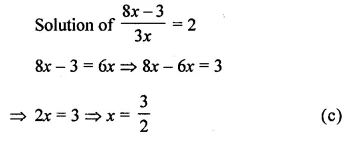
Question 9.
If we subtract \(\frac{1}{2}\) from a number and multiply the result by \(\frac{1}{2}\), we get \(\frac{1}{8}\), then the number is

Solution:
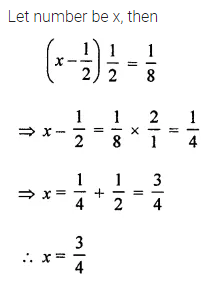
Question 10.
Fifteen years from now Ravi’s age will be four times his present age. What is Ravi’s present age?
(a) 4 years
(b) 5 years
(c) 6 years
(d) 3 years
Solution:
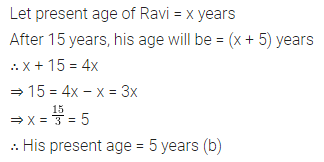
Question 11.
If the sum of three consecutive integers is 51, then the largest integer is
(a) 16
(b) 17
(c) 18
(d) 19
Solution:
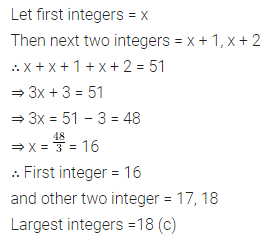
Question 12.
If the perimeter of a rectangle is 13 cm and its Width is \(2 \frac{3}{4}\) cm, then its length is

Solution:

Question 13.
What should be added to twice the rational number \(\frac{-7}{3}\) to get \(\frac{3}{7}\) ?

Solution:
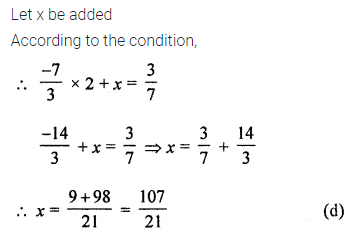
Question 14.
Sum of digits of a two digit number is 8. If the number obtained by reversing the digits is 18 more than the original number, then the original number is
(a) 35
(b) 53
(c) 26
(d) 62
Solution:
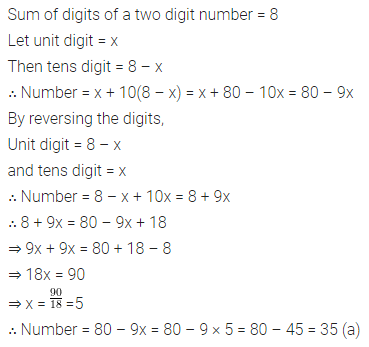
Question 15.
Arjun is twice as old as Shriya. If five years ago his age was three times Shriya’s age, then Arjun’s present age is
(a) 10 years
(b) 15 years
(c) 20 years
(d) 25 years
Solution:

Question 16.
If the replacement set is {-5, -3, -1,0, 1, 3}, then the solution set of the inequation -3 < x < 3 is
(a) {-2,-1, 0, 1, 2}
(b) {-1, 0, 1, 2}
(c) {-3,-1, 0, 1, 3}
(d) {-1,0, 1}
Solution:

Value Based Questions
Question 1.
Seema is habitual of saving her pocket money. She collected some 50 paise and 25 paise coins in her piggy bank. If she collected ₹25 and number of 50 paise coins is double the number of 25 paise coins. How many coins of each type did she collect? What values are being promoted? Is saving a good habit?
Solution:

Question 2.
Ramesh gave one fourth of his property to his two sons in equal shares and rest to his wife Sunita. Sunita gave one-third of her share to an orphanage. If the amount given by Sunita to the orphanage was ₹20000, find the total value of the Ramesh’s property and the amount each person got? What value is shown by the Sunita?
Solution:

Higher Order Thinking Skills (Hots)
Question 1.
A man covers a distance of 24 km in \(3 \frac{1}{2}\) hours partly on foot at the speed of 4.5 km/h and partly on bicycle at the speed of 10 km/h. Find the distance covered on foot.
Solution:

Question 2.
The perimeter of a rectangle is 240 cm. If its length is decreased by 10% and breadth is increased by 20% we get the same perimeter. Find the original length and breadth of the rectangle.
Solution:

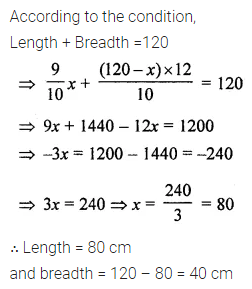
Question 3.
A person preparing a medicine wants to convert 15% alcohol solution into 32% alcohol solution. Find how much pure alcohol he should mix in 400 mL of 15% alcohol solution to obtain required solution?
Solution:
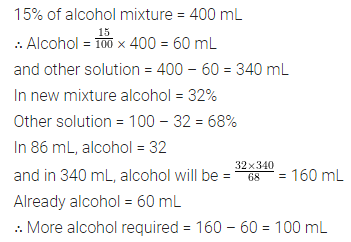
Question 4.
Rahul covers a distance from P to Q on a bicycle at 10 km/h and returns back at 9 km/h. Anuj covers the distance from P to Q and Q to P both at 12 km/h. On calculating we find that Anuj took 10 minutes less than Rahul. Find the distance between P and Q.
Solution:


Question 5.
Solve:
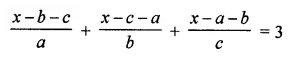
Solution:
