ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4

Question 1.
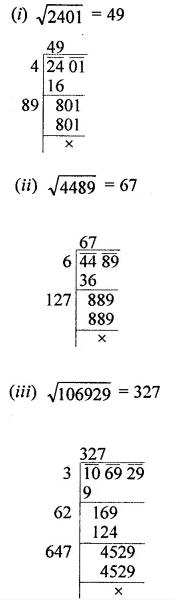
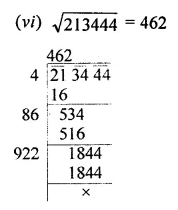
Find the square root of each of the following by division method:
(i) 2401
(ii) 4489
(iii) 106929
(iv) 167281
(v) 53824
(vi) 213444
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 1

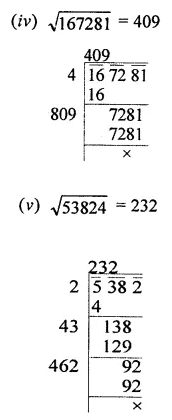
Question 2.
Find the number of digits in the square root of each of the following (without any calculation):
(i) 81
(ii) 169
(iii) 4761
(iv) 27889
(v) 525625
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 4

Question 3.
Find the square root of the following decimal numbers by division method:
(i) 51.84
(ii) 42.25
(iii) 18.4041
(iv) 5.774409
Solution:
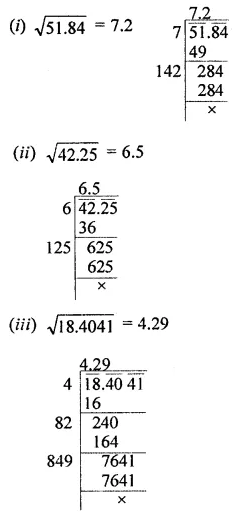
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 5

Question 4.
Find the square root of the following numbers correct to two decimal places:
(i) 645.8
(ii) 107.45
(iii) 5.462
(iv) 2
(v) 3
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 6

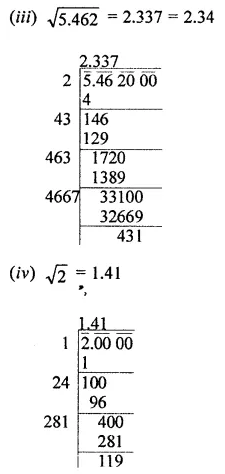
Question 5.
Find the square root of the following fractions by division method:
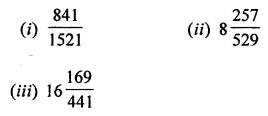
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 9
Solution:

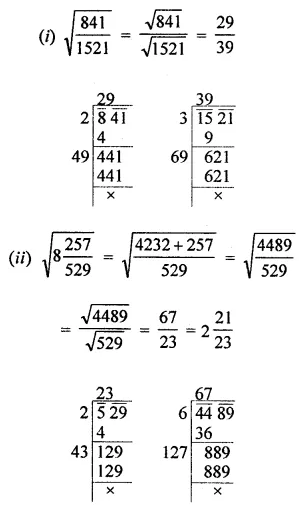
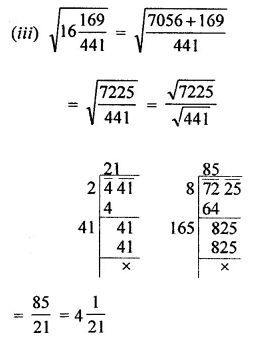
Question 6.
Find the least number which must be subtracted from each of the following numbers to make them a perfect square. Also find the square root of the perfect square number so obtained:
(i) 2000
(ii) 984
(iii) 8934
(iv) 11021
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 12

Question 7.
Find the least number which must be added to each of the following numbers to make them a perfect square. Also find the square root of the perfect square number so obtained:
(i) 1750
(ii) 6412
(iii) 6598
(iv) 8000
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 14

Question 8.
Find the smallest four-digit number which is a perfect square.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 17

Question 9.
Find the greatest number of six digits which is a perfect square.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 18

Question 10.
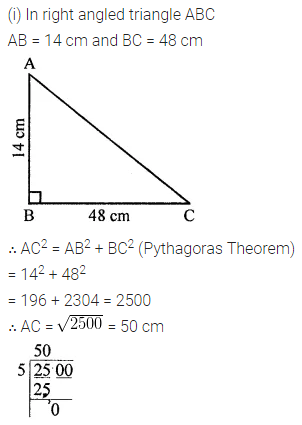
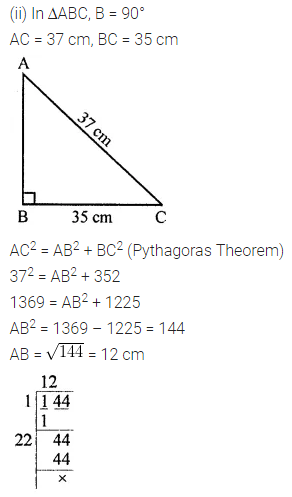
In a right triangle ABC, ∠B = 90°.
(i) If AB = 14 cm, BC = 48 cm, find AC.
(ii) If AC = 37 cm, BC = 35 cm, find AB.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 19

Question 11.
A gardener has 1400 plants. He wants to plant these in such a way that the number of rows and number of columns remains the same. Find the minimum number of plants he needs more for this.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 21

Question 12.
There are 1000 children in a school. For a P.T. drill they have to stand in such a way that the number of rows is equal to a number of columns. How many children would be left out in this arrangement?
Solution:
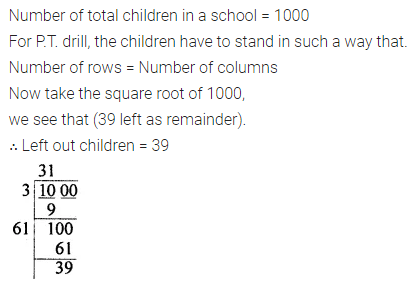
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 22

Question 13.
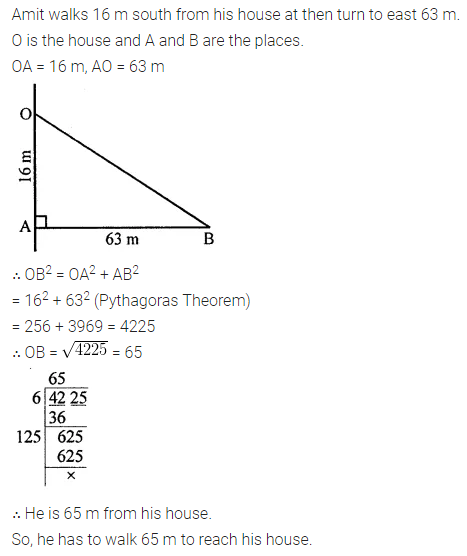
Amit walks 16 m south from his house and turns east to walk 63 ra to reach his friend’s house. While returning, he walks diagonally from his friend’s house to reach back to his house. What distance did he walk while returning?
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 23

Question 14.
A ladder 6 m long leaned against a wall. The ladder reaches the wall to a height of 4.8 m. Find the distance between the wall and the foot of the ladder.
Solution:
ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 3 Squares and Square Roots Ex 3.4 24