ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 5 Playing with Numbers Objective Type Questions
Mental Maths
Question 1.
Fill in the blanks:
(i) The sum of a 2-digit number and number obtained by reversing the digits is always divisible by 11 and ……….
(ii) The difference of a 2-digit number and number obtained by reversing the digits is always divisible by ………. and ……….
(iii) The difference of a 3=digit number a b c (a > c) and the number obtained by reversing the digits is always divisible by ………. and ……….
(iv) The next number of the series 0, 1, 1, 2, 3, 5, 8, 13, ………. is ……….
(v) General form of a 2 digit number 57 is ……….
(vi) Usual form of number 100 × 7 + 10 × 4 + 1 is ……….
(vii) If the division N ÷ 5 leaves remainder 4 and the division N ÷ 2 leaves remainder 1, then unit’s digit of N must be ……….
(viii)If 213×52 is divisible by 9, then digit x is ……….
Solution:

Question 2.
State whether the following statements are true (T) or false (F):
(i) If the division N ÷ 5 leaves a remainder 4, then unit’s digit of N may be 1 or 6.
(ii) If the division N ÷ 2 leaves a remainder 1, then unit’s digit of N may be 1, 3, 5, 7 or 9.
(iii) If a number is divisible by any number m, then it will also be divisible by each of the factors of m.
(iv) If a number is divisible by sum of two numbers then it will also be divisible by each of the two numbers separately.
(v) If 3651x is divisble by 9, then value of digit x is 3.
(vi) If 42×7 is divisible by 3, then value of digit x is 4.
(vii) The number 152875 is divisible by 9.
(viii)The number 389072 is divisible by 8.
(ix) The number 27402 is divisible by 6.
(x) The number 359249 is not divisible by 11.
Solution:


Multiple Choice Questions
Choose the correct answer from the given four options (3 to 13):
Question 3.
When the sum of a 2-digit number ab and number obtained by reversing the digits is divided by (a + b), the quotient is
(a) a – b
(b) 9
(c) 11
(d) None of these
Solution:
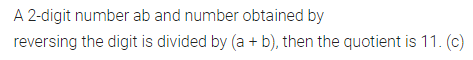
Question 4.
When the sum of a 3-digit number abc and numbers obtained by changing the order of the digits cyclically is divided by 111, then the quotient is
(a) 37
(b) a – b + c
(c) a + b + c
(d) 3
Solution:
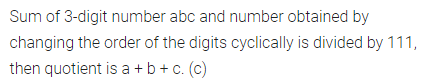
Question 5.
If A + A + A = BI, where A and B are different digits, then
(a) A = 1, B = 5
(b) A = 5, B = 2
(c) A = 5, B = 1
(d) A = 7, B = 2
Solution:

Question 6.
Which of the following numbers is not divisible by 2?
(a) 437218
(b) 437821
(c) 437812
(d) 437182
Solution:

Question 7.
Which of the following numbers is not divisible by 10?
(a) 32570
(b) 32750
(c) 32500
(d) 32075
Solution:

Question 8.
Which of the following numbers is divisible by 4?
(a) 98764
(b) 98746
(c) 98674
(d) 98647
Solution:

Question 9.
Which of the following numbers is divisible by 8?
(a) 32466
(b) 32476
(c) 32486
(d) 32456
Solution:

Question 10.
Which of the following numbers is divisible by 11?
(a) 725824
(b) 752824
(c) 725842
(d) 725482
Solution:

Question 11.
Which of the following numbers is not divisible by 9?
(a) 24354
(b) 24453
(c) 24534
(d) 24564
Solution:

Question 12.
If 467×8 is divisible by 3, then the value of x
(a) 1
(b) 2
(c) 3
(d) 4
Solution:

Question 13.
If 36x52y8 is divisible by 9, then x + y is
(a) 2
(b) 3
(c) 4
(d) 5
Solution:
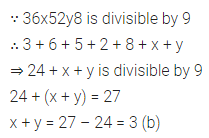
Value Based Question
Question 1.
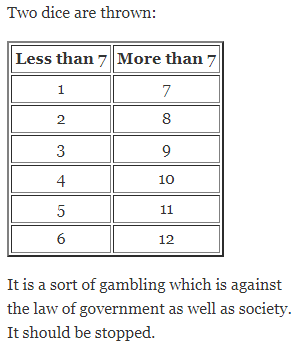
Rishabh plays a game with two dice in a fete. He draws three columns on a chart paper. In the left-most column, he writes the digits less than 7 and in the rightmost column he writes the numbers greater than 7. In the middle column, he writes digit 7 only. He offers people to keep money on any one of the columns. He throws two dice together if the sum of the digits on the two dice is less than 7, he doubles the money kept on the left-most column and collect the money kept on the remaining two columns. Similarly, he doubles the money on a rightmost column if the sum of digits is greater than 7 and triples on the middle column if the sum of the digits is 7. What digits should he write on leftmost and rightmost columns?
Is this game a sort of gambling? Is gambling a good way of earning money?
Solution:
Higher Order Thinking Skills (Hots)
Question 1.
If the difference of two-digit number and number obtained by reversing the digits is 45, then write all possible 2-digit numbers.
Solution:
