ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 6 Operation on sets Venn Diagrams Check Your Progress
Question 1.
If ξ={x : x ϵ N, r < 25} and A = {x : x is a composite number}, then find A’ in set builder from and also in roster form.
Solution:

Question 2.
If ξ = {x | x ϵ I, -5 ≤ x ≤ 5}, A = {-5, -3, 0, 3, 5} and B = {-4, -2, 0, 2, 4}, then
(i) Find A ∪ B and A ∩ B
(ii) Verify that n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
(iii) Find A’ and verify that n(A) + n(A’) = n(ξ).
(iv) Find B’ and verify that n(B’) = n(ξ) – n(B)
(v) Find A ∪ A’, A ∩ A’, B ∪ B’ and B ∩ B’.
(vi) Find (A ∪ B)’ and A’ ∩ B’. Are they equal ?
(vii) Find (A ∩ B)’ and A’ ∪ B’. Are they equal ?
Solution:
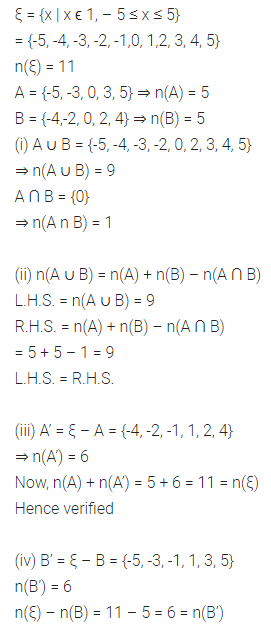

Question 3.
If ξ = {x | x ϵ N, x ≤ 12}, A = {prime numbers} and B = {odd numbers}, then
(i) Find A ∪ B and A ∩ B.
(ii) Verify that n(A ∪ B) + n(A ∩ B) = n(A) + n(B).
(iii) Find A’ and B’.
(iv) Find (A ∪ B)’ and verify that n(A ∪ B) + n(A ∪ B)’ = n(ξ).
(v) Find (A ∩ B)’ and A’ ∪ B’. Are they equal ?
Solution:


Question 4.
If ξ = {x : x ϵ N, x ≤ 12}, A= {x : x ≥ 7} and B = {x : 4 < x < 10}. Find :
(i) A’
(ii) B’
(iii) A ∪ B
(iv) A ∩ B
(v) A – B
(vi) B – A
(vii) (A ∪ B)’
(viii) A’ ∩ B’
Also verify that:
(i) (A ∪ B)’ = A’ ∩ B’
(ii) A – B = A ∩ B’
(iii) n(A ∪ B) + n((A ∪ B)’) = n(ξ)
(iv) n(A ∪ B) = n(A – B) + n(B – A) + n(A ∩ B).
Solution:



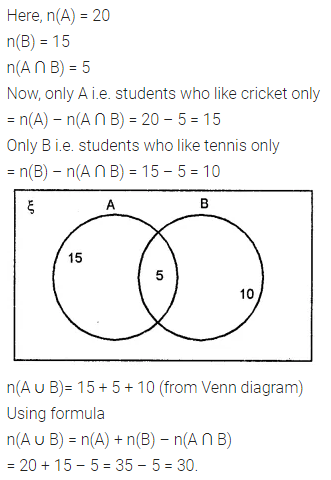
Question 5.
Given A = {students who like cricket} and B = {students who like tennis}; n(A) = 20, n(B) = 15 and n(A ∩ B)= 5.
Illustrate this through a Venn diagram. Hence find n(A ∪ B).
Solution:
Question 6.
If n(ξ) = 50, n(A) = 15, n(B) = 13 and n(A ∩ B) = 10. Find n(A’), n(B’) and n(A ∪ B).
Solution:
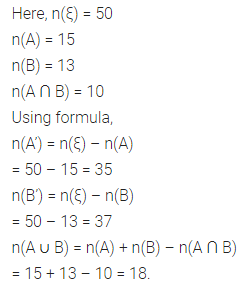
Question 7.
If n(ξ) = 60, n(A) = 35, n(B’) = 36 and n((A ∩ B)’) = 51, find :
(i) n(B)
(ii) n(A ∩ B)
(iii) n(A ∪ B)
(iv) n(A – B)
Solution:

Question 8.
In a city, 50% of people read newspaper A, 45% read newspaper B, and 25% read neither A nor B. What percentage of people read both the newspapers A as well as B?
Solution:
