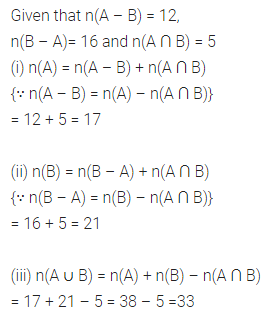ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 6 Operation on sets Venn Diagrams Ex 6.1

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 6 Operation on sets Venn Diagrams Ex 6.1

Question 1.
If A = {0, 1, 2, 3, …….., 8}, B = {3, 5, 7, 9, 11} and C = {0, 5, 10, 20}, find
(i) A ∪ B
(ii) A ∪ C
(iii) B ∪ C
(iv) A ∩ B
(v) A ∩ C
(vi) B ∩ C
Also find the cardinal number of the sets B ∪ C, A ∪ B, A ∩ C and B ∩ C.
Solution:

Question 2.
Find A’ when
(i) A= {0, 1, 4, 7} and E, = {x | x ϵ W, x ≤ 10}
(ii) A = {consonants} and ξ = {alphabets of English}
(iii) A = boys in class VIII of all schools in Bengaluru} and ξ = {students in class VIII of all schools in Bengaluru}
(iv) A = {letters of KALKA} and ξ = {letters of KOLKATA}
(v) A = {odd natural numbers} and ξ = {whole numbers}.
Solution:

Question 3.
If A {x : x ϵ N and 3 < x < 1} and B = {x : x ϵ Wand x ≤ 4}, find
(i) A ∪ B
(ii) A ∩ B
(iii) A – B
(iv) B – A
Solution:

Question 4.
If P = {x : x ϵ W and x < 6} and Q = {x : x ϵ N and 4 ≤ x ≤ 9}, find
(i) P ∪ Q
(ii) P ∩ Q
(iii) P – Q
(iv) Q – P
Is P ∪ Q a proper superset of P ∩ Q ?
Solution:

Question 5.
If A = (letters of word INTEGRITY) and B = (letters of word RECKONING), find
(i) A ∪ B
(ii) A ∩ B
(iii) A – B
(iv) B – A
Also verify that:
(a) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
(b) n(A – B) = n(A ∪ B) – n(B)
= n(A) – n(A ∪ B)
(c) n(B – A) = n(A ∪ B) – n(A)
= n(B) – n(A ∩ B)
(d) n(A ∪ B) = n(A – B) + n(B – A) + n(A ∩ B).
Solution:

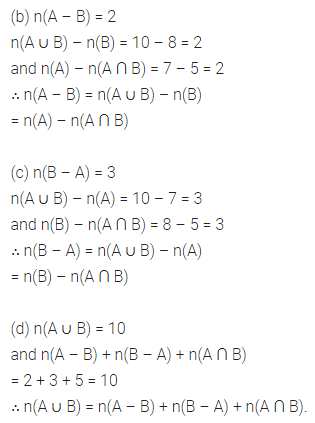
Question 6.
If ξ = {natural numbers between 10 and 40}
A = {multiples of 5} and
B = {multiples of 6}, then
(i) find A ∪ B and A ∩ B
(ii) verify that
n(A ∪ B) = B (A) + n(B) – n(A ∩ B).
Solution:

Question 7.
If ξ ={1,2, 3, …. 9}, A = {1, 2, 3, 4, 6, 7, 8} and B = {4, 6, 8}, then find.
(i) A’
(ii) B’
(iii) A ∪ B
(iv) A ∩ B
(v) A – B
(vi) B – A
(vii) (A ∩ B)’
(viii) A’ ∪ B’
Also verify that:
(a) (A ∩ B)’ = A’ ∪ B’
(b) n(A) + n(A’) = n(ξ)
(c) n(A ∩ B) + n((A ∩ B)’) = n(ξ)
(d) n(A – B) + n(B – A) + n(A ∩ B)
= n(A ∪ B).
Solution:

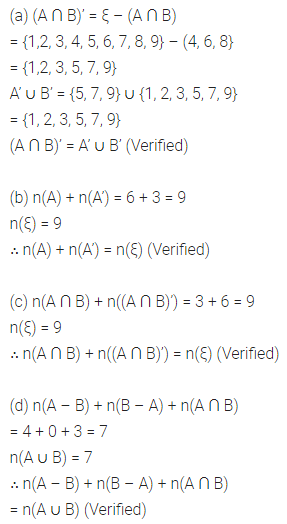
Question 8.
If 4 = {x : x ϵ W, x ≤ 10}, A. = {x : x ≥ 5} and B = {x : 3 ≤ x < 8}, then verify that:
(i) (A ∪ B)’ = A’ ∩ B’
(ii) (A ∩ B)’= A’ ∪ B’
(iii) A – B = A ∩ B’
(iv) B – A = B ∩ A’
Solution:

Question 9.
If n(A) = 20, n(B) = 16 and n(A ∪ B) = 30, find n(A ∩ B).
Solution:

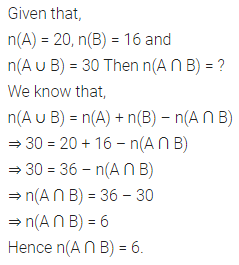
Question 10.
If n ξ = 20 and n(A’) = 7, then find n(A).
Solution:

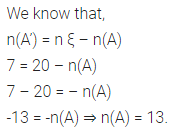
Question 11.
If n(ξ) = 40, n(A) = 20, n(B’) = 16 and n(A ∪ B) = 32, then find n(B) and n(A ∩ B).
Solution:

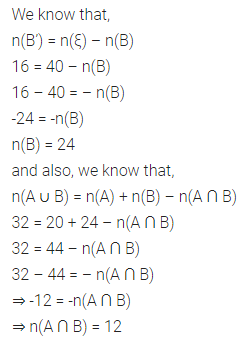
Question 12.
If n(ξ) = 32, n(A) = 20, n(B) = 16 and n((A ∪ B)’) = 4, find :
(i) n(A ∪ B)
(ii) n(A ∩ B)
(iii) n(A – B)
Solution:

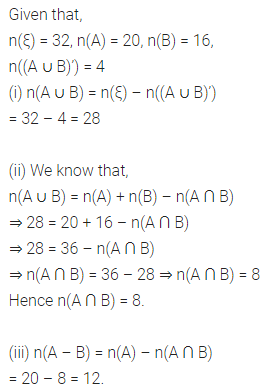
Question 13.
If n(ξ) = 40, n(A’) = 15, n(B) = 12 and n((A ∩ B)’) = 32, find :
(i) n(A)
(ii) n(B’)
(iii) n(A ∩ B)
(iv) n(A ∪ B)
(v) n(A – B)
(vi) n(B – A)
Solution:

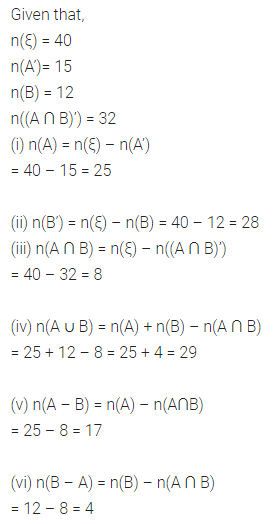
Question 14.
If n(A – B) = 12, n(B – A) = 16 and n(A ∩ B) = 5, find:
(i) n(A)
(ii) n(B)
(iii) n(A ∪ B)
Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths