NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2

NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 11
Chapter Name	Constructions
Exercise	Ex 11.2
Number of Questions Solved	7
Category	NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2

In each of the following, give the justification of the construction also:

Question 1.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:
Steps of Construction:
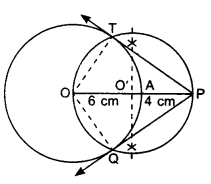
1. Draw a circle of radius 6 cm.
2. Mark a point P at a distance 10 cm from the centre O.
3. Here OP = 10 cm, draw perpendicular bisector of OP, which intersects OP at O’.
4. Take O’ as centre, draw a circle of radius O’O, which passes through O and P and intersects the previous circle at points T and Q.
5. Join PT and PQ, measure them, these are the required tangents.

Justification:
Join OT and OQ.

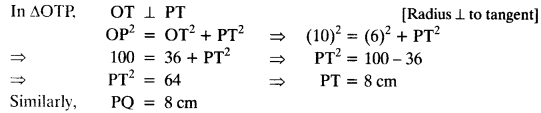
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ PT = PQ.

Question 2.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution:
Steps of Construction:
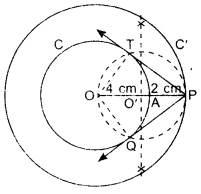
1. Draw concentric circles of radius OA = 4 cm and OP = 6 cm having same centre O.
2. Mark these circles as C and C’.
3. Points O, A and P lie on the same line.
4. Draw perpendicular bisector of OP, which intersects OP at O’.
5. Take O’ as centre, draw a circle of radius OO’ which intersects the circle C at points T and Q.
6. Join PT and PQ, these are the required tangents.
7. Length of these tangents are approx. 4.5 cm.

Justification:
Join OT and OQ.

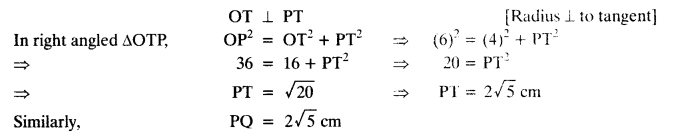
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ PT = PQ.

Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution:
Steps of Construction:

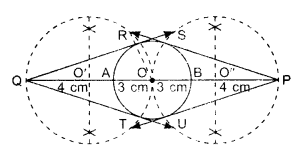
1. Draw a circle of radius 3 cm, having centre O. Mark this circle as C.
2. Mark points P and Q along its extended diameter such that OP = 7 cm and OQ = 7 cm.
3. Draw perpendicular bisector of OQ, intersecting OQ at O’.
4. Draw perpendicular bisector of OP intersecting OP at O”.
5. Take O’ as centre and draw a circle of radius OO’ which passes through points O and Q, intersecting circle C at points R and T.
6. Take O” as centre and draw a circle of radius O”P which passes through points O and P, intersecting the, circle C at points S and U.
7. Join QR and QT; PS and PU, these are the required tangents.
Justification:
Join OR.
In ∆OQR,
OR ⊥ QR [Radius ± to tangent]
OQ² = OR² + QR²
⇒ (7)² = (3)² + QR² ⇒ 49 = 9 + OR²
⇒ 40 = QR² ⇒ QR = 2 \(\sqrt{10}\) cm
Similary,
QT = 2 \(\sqrt{10}\) cm
PS = 2 \(\sqrt{10}\) cm
PU = 2 \(\sqrt{10}\) cm
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ QR = QT and PS = PU

Question 4.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution:
Steps of Construction:

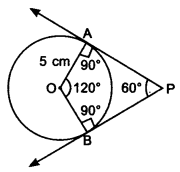
1. Draw a circle of radius 5 cm.
2. As tangents are inclined to each other at an angle of 60°.
∴ Angle between the radii of circle is 120°. (Use quadrilateral property)
3. Draw radii OA and OB inclined to each other at an angle 120°.
4. At points A and B, draw 90° angles. The arms of these angles intersect at point P.
5. PA and PB are the required tangents.
Justification:
In quadrilateral AOBP,
AP and BP are the tangents to the circle.
Join OP.
In right angled AOAP, OA ⊥ PA [Radius is ⊥ to tangent]

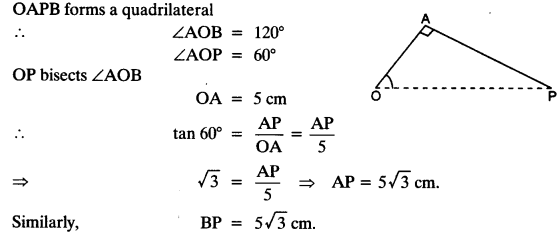
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ PA = PB

Question 5.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution:
Steps of Construction:

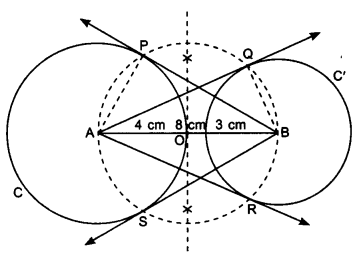
1. Draw a line segment AB = 8 cm.
2. Taking A as centre draw a circle C of radius 4 cm and taking B as centre draw a circle C’ of radius 3 cm.
3. Draw perpendicular bisector of AB, which intersects AB at point O.
4. Taking point O as centre draw a circle of radius 4 cm passing through points A and B which intersect circle C at P and S and circle C’ at points R and Q.
5. Join AQ, AR, BP and BS. These are the required tangents.
Justification:
Join AP.

A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ AQ = AR and BP = BS.

Question 6.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ZB = 90°. BD is the perpendicular Burn B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:
Steps of Construction:
1. Draw a right triangle ABC with AB = 6 cm, BC = 8 cm and ZB = 90°.
2. From B, draw BD perpendicular to AC.
3. Draw perpendicular bisector of BC which intersect BC at point O’.
4. Take O’ as centre and O’B as radius, draw a circle C’ passes through points B, C and D.

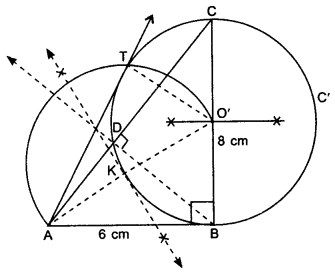
5. Join O’A and draw perpendicular bisector of O’A which intersect O’A at point K.
6. Take K as centre, draw an arc of radius KO’ intersect the previous circle C’ at T.
7. Join AT, AT is required tangent.
Justification:
∠BDC = 90°
∴ BC acts as diameter.
AB is tangent to circle having centre O’

A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ AB = AT.

Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution:
Steps of Construction:
1. Draw a circle C’ with the help of a bangle, for finding the centre, take three non-collinear points A, B and C, lying on the circle. Join AB and BC and draw perpendicular bisector of AB and BC, both intersect at a point O,
‘O’ is centre of the circle.

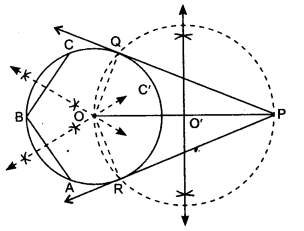
2. Take a point P outside the circle. Join OP.
3. Draw perpendicular bisector of OP, which intersects OP at point O’.
4. Take O’ as the centre with OO’ as radius draw a circle which passes through O and P, intersecting previous circle C’ at points R and Q.
5. Join PQ and PR.
6. PQ and PR are the required pair of tangents.
Justification:
Join OQ and OR.
In AOQP and AOPR, OQ = OR [Radii of the circle]
OP = OP [Common]
∠Q = ∠R = 90° [Radius is ⊥ to tangent]
∆OQP ≅ ∆ORP [by RHS]
∴ PQ = PR [By C.P.C.T]
A pair of tangents can be drawn to a circle from an external point lying outside the circle. These two tangents are equal in lengths.
∴ PQ = PR

We hope the NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2, drop a comment below and we will get back to you at the earliest.