NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 11 |
| Chapter Name | Constructions |
| Exercise | Ex 11.1 |
| Number of Questions Solved | 7 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1
In each of the following, give the justification of the construction also:
Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Solution:
Steps of Construction:
1. Draw a line segment AB = 7.6 cm.
2. Draw an acute angle BAX on base AB. Mark the ray as AX.
3. Locate 13 points A1, A2, A3, …… , A13 on the ray AX so that AA1 = A1A2 = ……… = A12A13
4. Join A13 with B and at A5 draw a line ∥ to BA13, i.e. A5C. The line intersects AB at C.
5. On measure AC = 2.9 cm and BC = 4.7 cm.
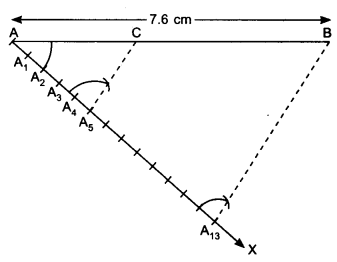
Justification:
In ∆AA5C and ∆AA13B,

∴ AC : BC = 5 : 8
Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac { 2 }{ 3 }\) of the corresponding sides of the first triangle.
Solution:
Steps of Construction:
1. Construct a ΔABC with AB = 4 cm, BC = 6 cm and AC = 5 cm.
2. Draw an acute angle CBX on the base BC at point B. Mark the ray as BX.
3. Mark the ray BX with B1, B2, B3 such that
BB1 = B1B2 = B2B3
4. Join B3 to C.
5. Draw B2C’ ∥ B3C, where C’ is a point on BC.
6. Draw C’A’ ∥ AC, where A’ is a point on BA.
7. ΔA’BC’ is the required triangle.
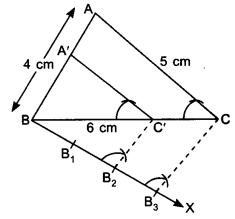
Justification: In ∆A’BC and ∆ABC,

Question 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are \(\frac { 7 }{ 5 }\) of the corresponding sides of the first triangle.
Solution:
Steps of Construction:
1. Draw a ΔABC with AB = 5 cm, BC = 7 cm and AC = 6 cm.
2. Draw an acute angle CBX below BC at point B.
3. Mark the ray BX as B1, B2, B3, B4, B5, B6 and B7 such that BB1= B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7.
4. Join B5 to C.
5. Draw B7C’ parallel to B5C, where C’ is a point on extended line BC.
6. Draw A’C’ ∥ AC, where A’ is a point on extended line BA.
A’BC’ is the required triangle.
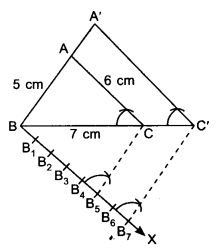
Justification: In ∆ABC and ∆A’BC’,

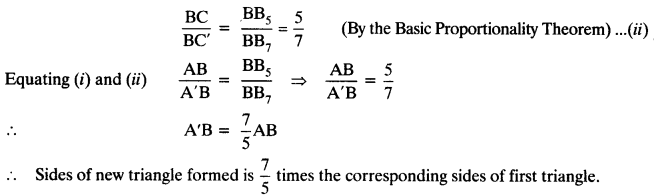
Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1\(\frac { 1 }{ 2 }\) times the corresponding sides of the isosceles triangle.
Solution:
Steps of Construction:
1. Draw base AB = 8 cm.
2. Draw perpendicular bisector of AB. Mark CD = 4 cm, on ⊥ bisector where D is mid-point on AB.
3. Draw an acute angle BAX, below AB at point A.
4. Mark the ray AX with A1, A2, A3 such that AA1 =A1A2 = A2A3
5. Join A2 to B. Draw A3B’ ∥ A2 B, where B’ is a point on extended line AB.
6. At B’, draw B’C’ 11 BC, where C’ is a point on extended line AC.
7. ∆AB’C’ is the required triangle.
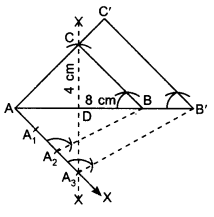
Justification: In ∆ABC and ∆A’BC’,

Question 5.
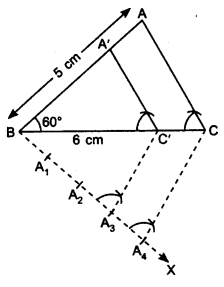
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are \(\frac { 3 }{ 4 }\) of the corresponding sides of the triangle ABC.
Solution:
Steps of Construction:
1. Draw a line segment BC = 6 cm and at point B draw an ∠ABC = 60°.
2. Cut AB = 5 cm. Join AC. We obtain a ΔABC.
3. Draw a ray BX making an acute angle with BC on the side opposite to the vertex A.
4. Locate 4 points A1, A2, A3 and A4 on the ray BX so that BA1 = A1A2 = A2A3 = A3A4.
5. Join A4 to C.
6. At A3, draw A3C’ ∥ A4C, where C’ is a point on the line segment BC.
7. At C’, draw C’A’ ∥ CA, where A’ is a point on the line segment BA.
∴ ∆A’BC’ is the required triangle.

Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are \(\frac { 4 }{ 3 }\) times the corresponding sides of ∆ABC.
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180°
⇒ 105° + 45° + ∠C = 180°
⇒ 150° + ∠C = 180°
⇒ ∠C = 30°
Steps of Construction:
1. Draw a line segment BC = 7 cm. At point B, draw an ∠B = 45° and at point C, draw an ∠C = 30° and get ΔABC.
2. Draw an acute ∠CBX on the base BC at point B. Mark the ray BX with B1, B2, B3, B4, such that BB1 = B1B2 = B2B3 = B3B4
3. Join B3 to C.
4. Draw B4C’ ∥ B3C, where C’ is point on extended line segment BC.
5. At C’, draw C’A’ ∥ AC, where A’ is a point on extended line segment BA.
6. ∆A’BC’ is the required triangle.
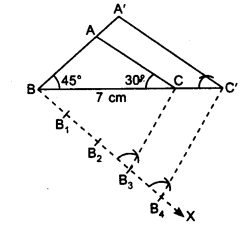
Justification: In ∆ABC and ∆A’BC’,
Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac { 5 }{ 3F }\) times the corresponding sides of the given triangle.
Solution:
Steps of Construction:
1. Draw a right angled ∆ABC with AB = 4 cm, AC = 3 cm and ∠A = 90°.
2. Make an acute angle BAX on the base AB at point A.
3. Mark the ray AX with A1, A2, A3, A4, A5 such that AA1 = A1A2 = A2A3 = A3A4 = A4A5.
4. Join A3B. At A5, draw A5B’ ∥ A3B, where B’ is a point on extended line segment AB.
5. At B’, draw B’C’ ∥ BC, where C’ is a point on extended line segment AC.
6. ∆AB’C’ is the required triangle.
Justification:
In ∆ABC and ∆AB’C’,
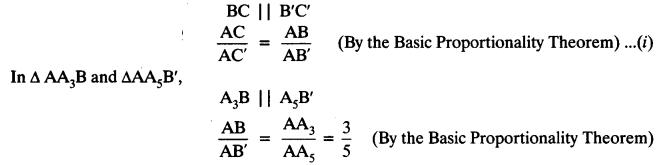
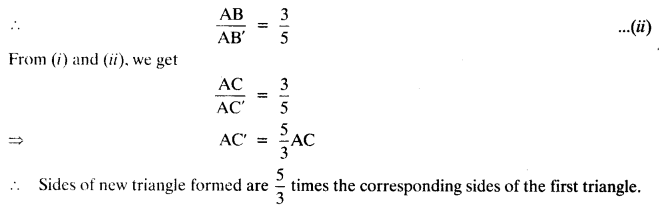
We hope the NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1, drop a comment below and we will get back to you at the earliest.