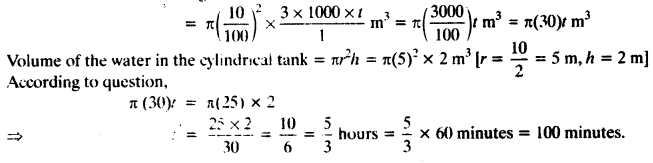NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.3 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.3.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 13 |
| Chapter Name | Surface Areas and Volumes |
| Exercise | Ex 13.3 |
| Number of Questions Solved | 9 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.3
Unless stated otherwise, take π = \(\frac { 22 }{ 7 }\)
Question 1.
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Solution:
Given: radius of metallic sphere = 4.2 cm
∴ Volume = \(\frac { 4 }{ 3 }\)π(4.2)³ …. (i)
∵ Sphere is melted and recast into a cylinder of radius 6 cm and height h.
∴ Volume of the cylinder =πr²h = π(6)² x h … (ii)
According to question,
Volume of the cylinder = Volume of the sphere
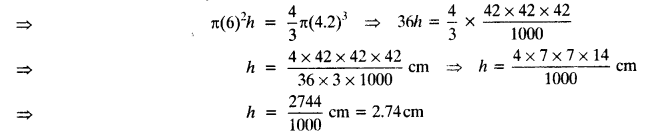
Question 2.
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Solution:
Radius of 1st metallic sphere = 6 cm
∴ Volume of 1st metallic sphere = \(\frac { 4 }{ 3 }\)π(6)³ cm³
Radius of 2nd metallic sphere = 8 cm
∴ Volume of 2nd metallic sphere = \(\frac { 4 }{ 3 }\)π(8)³ cm³
Radius of 3rd metallic sphere = 10 cm
∴ Volume of 3rd metallic sphere = \(\frac { 4 }{ 3 }\)π(10)³ cm³
Volume of all three metallic spheres = \(\frac { 4 }{ 3 }\)π(6³+8³+10³) cm³
∵ 3 spheres are melted and recast into a new metallic sphere of radius r.
∴ Volume of new metallic sphere = \(\frac { 4 }{ 3 }\)πr³
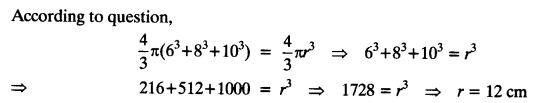
Question 3.
A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Solution:
Given: diameter of the well = 7 m Radius = \(\frac { 7 }{ 2 }\)m
and depth of the well = 20 m
Volume of the earth taken out from the well = πr²

Question 4.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
Solution:
Given: diameter of the well = 3 m
⇒ Radius = \(\frac { 3 }{ 2 }\)m
Depth of the well = 14 m
Volume of the earth taken out from the well = πr²h
= π(\(\frac { 3 }{ 2 }\))² x 14 = \(\frac { π×9×14 }{ 4 }\) = \(\frac { 63 }{ 2 }\)πm³
∵ Earth taken out from the well evenly spread to form an embankment having height h and width of embankment around the well is 4 m.
∴ External radius (R) = radius of well + width of the embankment
= \(\frac { 3 }{ 2 }\)m + 4m = \(\frac { 11 }{ 2 }\)m
Internal radius = \(\frac { 3 }{ 2 }\)m = radius of well
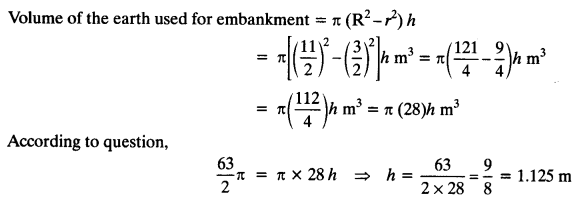
Question 5.
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Solution:

Let total number of ice cream cones are n.
∴ All ice cream cones are filled from ice cream in the cylinder.
Total volume of n number of ice cream cones = Volume of ice cream in the cylinder
n x π x 54 = π(36)15
⇒ n x 54 = 36 x 15
⇒ n = \(\frac { 36 × 15 }{ 54 }\) = 10
Question 6.
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm x 10 cm x 3.5 cm?
Solution:
Given: diameter of each coin = 1.75 cm ⇒ radius = \(\frac { 1.75 }{ 2 }\)cm
and thickness of each coin = 2 mm
Let n number of coins are melted to form a cuboid.
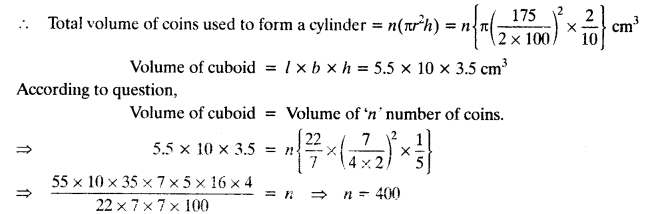
Question 7.
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Solution:
Given: radius of the cylindrical bucket = 18 cm
and height = 32 cm
∴ Volume of the cylindrical bucket = π²h = π(18)² x 32 cm³
Let radius of the conical heap = r cm
Given: height of the conical heap = 24 cm
∴ Volume of the conical heap = \(\frac { 1 }{ 3 }\)π(r²) 24cm³
According to question,
Volume of the cylinderical bucket = Volume of the conical heap

Question 8.
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Solution:
Given: width of canal = 6m, depth = 1.5 m
Rate of flowing water – 10 km/h
Volume of the water flowing in 30 minutes = \(\frac { 6×1.5×30×10 }{ 60 }\)km³
= \(\frac { 6×1.5×10×1000×30 }{ 10×60 }\)km³ = 45000 m³
We require water for standing up to height = 8 cm = \(\frac { 8 }{ 100 }\) m
Let the required area he A
∴ Volume of water required = A(\(\frac { 8 }{ 100 }\))m³
According to question. 45000 = \(\frac { A×8 }{ 100 }\)
⇒ \(\frac { 45000×100 }{ 8 }\) = A ⇒ A = 562500 m²
Question 9.
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in his Held, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Solution:
Given: diameter of the pipe = 20 cm ⇒ radius of the pipe = 10 cm
Water flowing from the pipe at rate = 3 km
Let it filled the tank in ‘t’ hours.
Volume of the water flowing in ‘t’ hours.