NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids

NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids

These Solutions are part of NCERT Solutions for Class 11 Physics. Here we have given NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids

Question 1.
Explain why
1. The blood pressure In humans is greater at the feet than at the brain.
Answer:
The height of the blood column in the human body is more at the feet than at the brain. As the pressure increases with the height of the column, blood exerts  more pressure at the feet than at the brain (P = ρgh)

2. Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than 100 km.
Answer:
The density of air is maximum near the surface of the earth (at sea level) and it decreases rapidly with height. The density of air at a height of 6 km reduces to almost half it’s value at sea level. Hence the atmospheric pressure at a height of 6 km decreases to nearly half of its value at sea level even though the height of the atmosphere is more than 100km.

3. Hydrostatic pressure is a scalar quantity even though pressure is force divided by area.
Answer:
The pressure created while applying a force on a liquid is transmitted equally in all direction inside the liquid. That is why there is no fixed direction for the pressure transmitted. Hence we can say that hydrostatic pressure is a scalar quantity.

Question 2.
Explain why
(a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute.
(b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets the glass while mercury does not.)
(c) Surface tension of a liquid is independent of the area of the surface.
(d) Detergents should have small angles of contact.
(e) A drop of liquid under no external forces is always spherical in shape.
Answer:
(a) The cohesive force between mercury molecules is greater than the adhesive force between mercury and glass molecules. Therefore, the meniscus of mercury in a glass tube is convex and hence the angle of contact is obtuse. In the case of water, the cohesive force between water molecules is less than the adhesive force between water and glass molecules. Therefore, the meniscus of water in the glass tube is concave and hence the angle of contact is acute.
(b) The cohesive force between water molecules is less than the adhesive force between glass and water molecules. On the other hand, the cohesive force between mercury molecules is greater than the adhesive force between glass and mercury molecules.
(c) Surface tension is defined as the force per unit length of an imaginary line drawn tangentially on the surface of the liquid at rest. Therefore, surface tension is also independent of the area of the liquid surface.
(d) So that the detergent has low surface tension and greater ability to wet a surface.
(e) In the absence of external force, liquid drop takes a spherical shape due to surface tension.

Question 3.
Fill in the blanks using the words from the list appended with each statement:
(a) Surface tension of liquids generally……………. with temperature (increases/decreases)
(b) Viscosity of gases……………… with temperature, whereas viscosity of liquids………………. with temperature (increases/decreases)
(c) For solids with the elastic modulus of rigidity, the shearing force is proportional to………………….. while for fluids it is proportional to…………. (shear strain/rate of shear strain)
(d) For a fluid in steady flow, the increase in flow speed at a constriction follows from…………….. while the decrease of pressure there follows from………….. (conservation of mass/Bernoulli’s principle)
(e) For the model of a plane in a wind tunnel, turbulence occurs at a…………………… speed than the critical speed for turbulence for an actual plane (greater/smaller)
Answer:
(a) decreases
(b) increases ; decreases
(c) shear strain ; rate of shear strain
(d) conservation of mass ; Bernoulli’s principle

Question 4.
Explain why
(a) To keep a piece of paper horizontal, you should blow over, not under, it.
(b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers.
(c) The size of a needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection.
(d) A fluid flowing out of a small hole in a vessel results in a backward thurst on the vessel.
(e) a spinning cricket ball in air does not follow a parabolic trajectory.
Answer:
(a) When we blow over the piece of paper, the velocity of air increases. As a result, the pressure over it decreases in accordance with the Bernoulli’s theorem whereas the pressure below it is higher (atmospheric pressure) which keeps the paper horizontal.

(b) This is due to the continuity equation of flow of the liquids. When we close the water tap, the area of cross-section decreases and according to the equation of continuity (aυ= constant), the velocity of flow of the liquid increases.

(c) For a> constant height, the Bernoulli’s theorem is expressed as
p + \(\frac { 1}{ 2 } \) pυ² = constant
In this equation, the pressure P occur with a single power whereas the velocity occurs with a square power. Therefore, the velocity has more effect compared to the pressure. It is for this reason that needle of the syringe controls flow rate better than the thumb pressure exerted by the doctor.

(d) When a fluid flows out of a small hole, it carries momentum with it. According to the law of conservation of momentum, the vessel gets a recoil momentum. Thus, there is a change in momentum of the vessel which means that a backward thurst acts on it.

(e) When ball is given spin at the top, the velocity of air above the ball is higher than below the ball. According to Bernoulli’s theorem, die pressure above the ball is less than the pressure below the ball. Thus, there is net upward force on the spinning ball and hence the ball follows a curved path. This effect is known as the Magnus effect.

Question 5.
A 50 kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter 1.0 cm. What is the pressure exerted by the heel on the horizontal floor?
Answer:
Mass of girl, m= 50 kg.
Force on the heel, F = mg = 50 x 9.8 = 490 N
Diameter, D = 1.0 cm = 1 x 10^-2 m

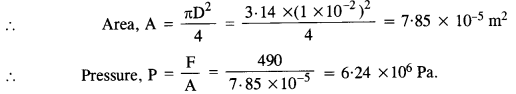
Question 6.
Toricelli’s barometer used mercury. Pascal duplicated it using French wine of density 984 kg m^-3. Determine the height of the wine column for normal atmospheric pressure.
Answer:
At normal pressure of atmosphere,


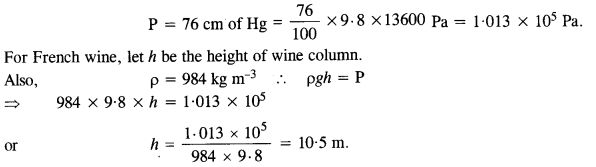
Question 7.
A vertical off-shore structure is built to withstand maximum stress of 10⁹ Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents.
Answer:
Maximum stress that can be taken by the off-share structure, P_max = 10⁹Pa.
density of water = 10³ kg /m³ and g = 9.8 m/s² and h = 3km (depth of the sea)
∴ Pressure exerted by seawater, P = ρgh
= 10³ × 9.8 × 3 × 10³
P = 2.94 × 10⁷ Pa
Note that, P < P_max
Since the pressure exerted by the seawater is less than the maximum pressure the structure can withstand, the structure is suitable for putting on the top of the oil well.

Question 8.
A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm². What maximum pressure would the smaller piston have to bear?
Answer:
Maximum mass, m= 3000 kg ; Area, A = 425 cm² = 425 x 10^-4 m².

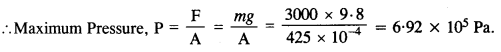
Question 9.
A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other. What is the specific gravity of spirit?
Answer:

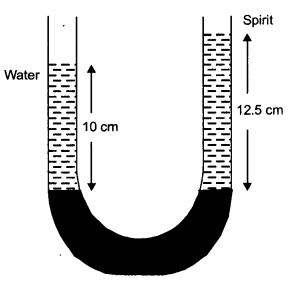
Since the mercury column in the two arms is in level, therefore,
Pressure due to spirit = Pressure due to water

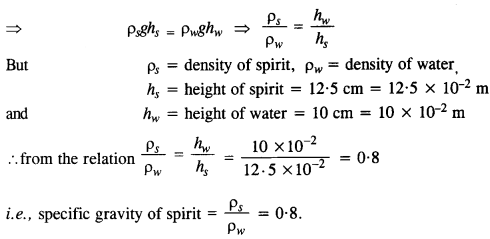
Question 10.
In the previous problem, if 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Specific gravity of mercury = 13.6)
Answer:
If p_m be the density of mercury, then

Question 11.
Can Bernoulli’s equation be used to describe the flow of water through a rapid motion in a river? Explain.
Answer:
No. The flow of water through a rapid in a river is turbulent and hence Bernoulli’s principle cannot be applied.

Question 12.
Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain.
Answer:
If the pressures at the two places where Bernoulli’s theorem is applied are not much different, it does not matter if one uses gauge pressure instead of absolute pressure.

Question 13.
Glycerine flows steadily through a horizontal tube of length 1.5 m and radius 1.0 cm. If the amount of glycerine collected per second at one end is 4.0 x 10^-3 kg s^-1, what is the pressure difference between the two ends of the tube? Density of glycerine = 1.3 X 10³ kg m^-3 and viscosity of
glycerine = 0.83 N s m^-2 to
Answer:
Here, l= 1.5 m, r =1.0 cm = 10^-2 q = 0.83 N s m^-2

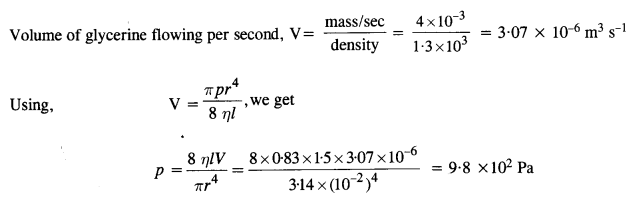
Question 14.
In a test experiment on a model airplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 m s^-1 and 63 m s^-1 respectively. What is the lift on the wing if its area is 2.5 m² ? Take the density of air to be 1.3 kg m^-3.
Answer:
Here υ₁ 70 ms^-1, υ₂ = 63 ms ‘, p = 1.3 kg m ³ and A = 2.5 m².
Now, using Bernoulli’s theorem (for constant height),

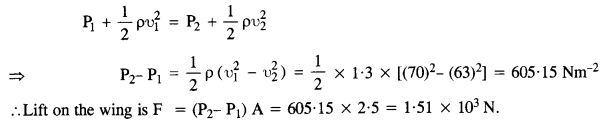
Question 15.
Figures (a) and (b) refer to the steady flow of a (non-viscous) liquid. Which of the two figures is incorrect? Why?

Answer:
Figure (a) is incorrect. It is because of the fact that at the kink, the velocity of flow of liquid is large and hence using the Bernoulli’s theorem the pressure is less. As a result, the water should not rise higher in the tube where there is a kink (i. e. where the area of cross-section is small).

Question 16.
The cylindrical tube of a spray pump has a cross-section of 8.0 cm² one end of which has 40 fine holes each of diameter 1.0 mm. If the liquid flow inside the tube is 1.5 m min^-1, what is the speed of ejection of the liquid through the holes ?
Answer:
Here, area of cylindrical tube, a_x = 8.0 cm² = 8 x 10^-4 m²

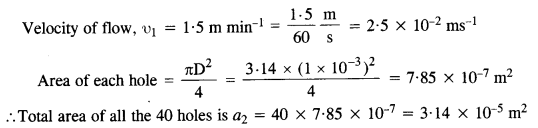
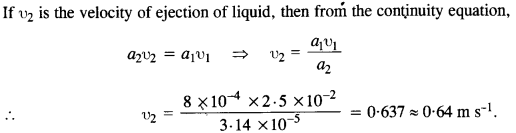
Question 17.
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 x 10^-2 N (which includes the small weight of the silder). The length of the silder is 30 cm. What is the surface tension of the film ?
Answer:
Force on the silder, F= 1.5 x 10^-2 N

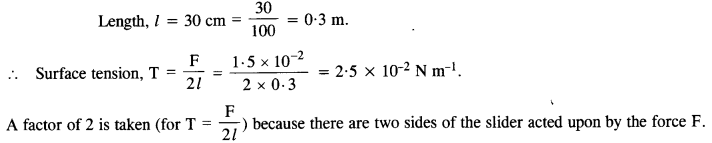
Question 18.
(a) shows a thin liquid film supporting a small weight = 4.5 x 10^-2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c) ? Explain your answer physically.

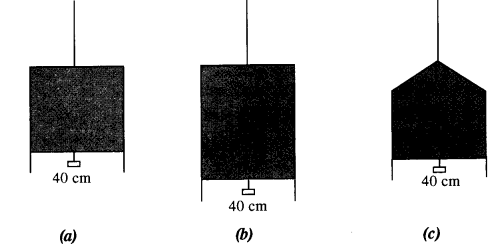
Answer:
As shown in fig(a)

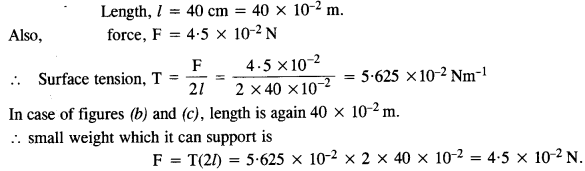
Question 19.
What is the pressure inside the drop of mercury of radius 3.00 mm at room temperature ? Surface tension of mercury at that temperature (20 °C) is 4.65 x 10^-1 N m^_1. The atmospheric pressure is 1.01 x 10⁵ Pa. Also give the excess pressure inside the drop.
Answer:
Here, surface tension, T = 4.65 x 10^-1 Nm^-1
Radius of drop, r =3.00 mm = 3 x 10^-3 m.
Outside pressure, p₀ = 1.01 x 10⁵ Pa.
Using the relation,

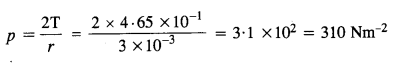
Question 20.
What is the excess pressure inside a bubble of soap solution of radius 5-00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 x 10^-2 N m^-1 ? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 x 10^s Pa).
Answer:
Here, surface tension, T = 2.50 x 10^-2 N m^-1
Radius, r= 5.00 mm = 5 x 10^-3 m.

Question 21.
A tank with a square base of area 1.0 m² is divided by a vertical partition in the middle. The bottom of the partition has a small-hinged door of area 20 cm². The tank is filled with water in one compartment, and an acid (or relative density 1.7) in the other, both to a height of 4.0 m. compute the force necessary to keep the door close.
Answer:

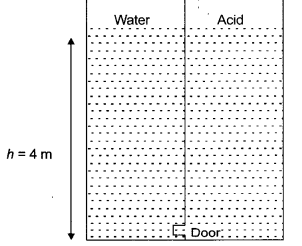
Question 22.
A manometer reads the pressure of a gas in an enclosure as shown in Fig. (a). When a pump removes some of the gas, the manometer reads as in Fig. (b). The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury.
(a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury.
(b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury) are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas).

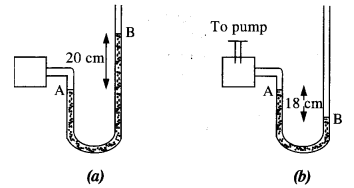
Answer:
The atmospheric pressure, P = 76 cm of mercury
(a) From figure (a),
Pressure head, h = 20 cm of mercury
∴ Absolute pressure = P + h = 76 + 20 = 96 cm of mercury
Also, Gauge pressure = h =20 cm of mercury
From figure (b),
Pressure head,h = -18 cm of mercury
∴ Absolute pressure = P + h = 76 + (- 18) = 58 cm of mercury
Also, (Gauge pressure = h = – 18 cm of mercury
(b) When 13.6 cm of water is poured into the right limb of the manometer of figure (b), then, using the relation : pressure, p = pgh = p’g’h’,

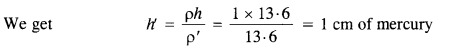
Therefore, pressure at the point B,
P_B = P + h’ = 76 + 1 = 77 cm of mercury
If h is the difference in the mercury levels in the two limbs, then taking P_A = P_B
=>  58 + h” = 11 => h” = 77 – 58 = 19 cm of mercury.

Question 23.
Two vessels have the same area but different shapes. The first vessel takes twice the volume of water that the second vessel requires to fill upto a particular common height. Is the force exerted by the water on the base of the vessel the same in the two cases? If so, why do the vessels filled with water to that same height give different readings on a weighing scale?
Answer:

Question 24.
During blood transfusion, the needle is inserted in a vein where the gauge pressure is 2000 Pa. At what height must the blood container be placed so that blood may just enter the vein ? [Use the density of whole blood as 1.06 x 10³ kg m^-3 ]
Answer:

Question 25.
In deriving Bernoulli’s equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy,
(a) How does the pressure change as the fluid moves along the tube if dissipative forces are present?
(b) Do the dissipative forces become more important as the fluid velocity increases? Discuss qualitatively.
Answer:
(a) If the dissipative forces are present, some of the pressure energy of the liquid is used in doing some work against these forces. Hence, the fluid pressure decreases.
(b) With the increase in velocity, the rate of loss of energy also increases. As a result, the dissipative forces become more significant.

Question 26.
(a) What is the largest average velocity of blood flow in an artery of radius 2 x 10^-3 m if the flow must remain steady? (b) What is the corresponding flow rate?
(Take viscosity of blood to be 2.084 x 10^-3 Pa s). Take the density of blood as 1.06 kg m^-3.
Answer:
Here, r = 2 x 10^-3 m, η = 2.084 x 10^-3 Pa s
Taking the maximum value of Reynold number for streamlined flow as N_R = 2000, the maximum velocity is

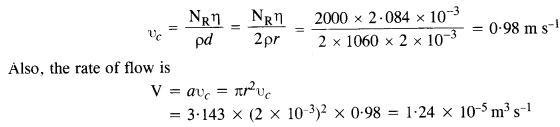
Question 27.
A plane is in level flight at constant speed and each of its two wings has an area of 25 m². If the speed of the air is 180 km/h over the lower wing and 234 km/h over the upper wing surface, determine the plane’s mass. (Take air density to be 1 kg m^-3).
Answer:

Question 28.
In Millikan’s oil drop experiment, what is the terminal speed of an uncharged drop of radius 2.0 x 10^-5 m and density 1.2 x 10³ kg m^-3. Take the viscosity of air at the temperature of the experiment to be
1.8 x 10^-5 How much is the viscous force on the drop at that speed ? Neglect buoyancy of the drop due to air.
Answer:

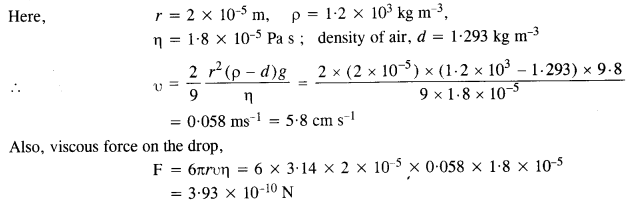
Question 29.
Mercury has an angle of contact equal to 140° with soda lime glass. A narrow tube of radius 1.00 mm made of this glass is dipped in a trough containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside ? Surface tension of mercury at the temperature of the experiment is 0.465 N m^_1. Density of mercury = 13.6 x 10³ kg m³.
Answer:
Here, angle of contact, θ = 140°                 .’. cos θ= cos 140° = – 0.7660
Also,  r = 1.00 mm = 1 x 10^-3 m, surface tension, T = 0.465 N nr¹
density ρ= 13.6 x 10³ kg m^-3

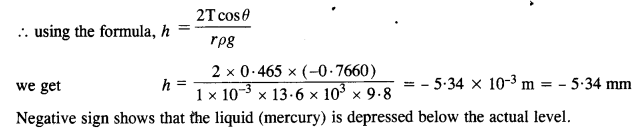
Question 30.
Two narrow bores of diameters 3.0 mm and 6.0 mm are joined together to form a U-tube open at both ends. If the U-tube contains water, what is the difference in its levels in the two limbs of the tube ? Surface tension of water at the temperature of the experiment is 7.3 x 10^-2 N m^-1. Take the angle of contact to be zero and density of water to be 1.0 x 10³ kg m^-3 (g = 9.8 ms’²)
Answer:
Let r_x be the radius of one bore and r₂ be the radius of second bore of the U-tube. Then, if h_x and h₂ are the heights of water on two sides,

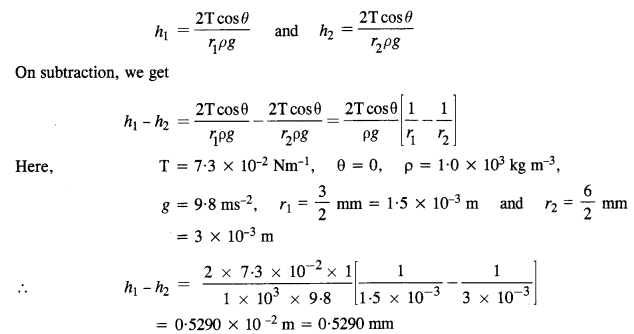
Question 31.
(a) It is known that density p of air decreases with height y (in metres) as

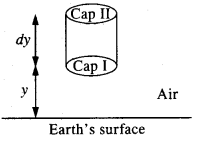
where ρo = 1.25 kg m^-3 is the density at sea level, and y₀ is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of the atmosphere remains constant (isothermal conditions). Also, assume that the value of g remains constant.
(b) A large He balloon of volume 1425 m³ is used to lift a payload of 400 kg. Assume that the balloon maintains a constant radius as it rises. How high does it rise?
[Take yo = 8000 m and p_He = 0.18 kg m^-3]
Answer:
(a) Consider an imaginary cylinder of air having an area ‘a’ of a cross-section of each end face and placed vertically above the surface of the earth. Let the cap I of the cylinder be at a height of y and the cap II be at the height y + dy. Let P and P + dP be the pressures at caps I and II respectively. Then, the net force acting on the cap due to gravity is the weight of the cylinder i. e.,
W = mass of cylinder xg = ady.pg    …(1)
Since the cylinder is considered to be placed in the air, therefore, the force due to the difference in pressure is balanced by the weight of the cylinder under the equilibrium conditions.

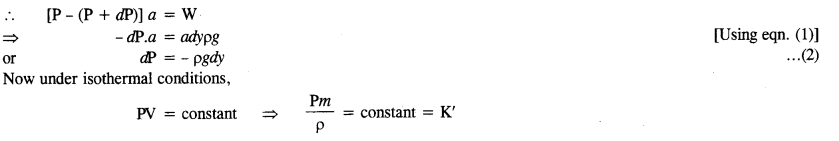
We hope the NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids, help you. If you have any query regarding NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids, drop a comment below and we will get back to you at the earliest