NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Number Systems |
| Exercise | Ex 1.3 |
| Number of Questions Solved | 9 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3
Question 1.
Write the following in decimal form and say what kind of decimal expansion each has
![]()
Solution:
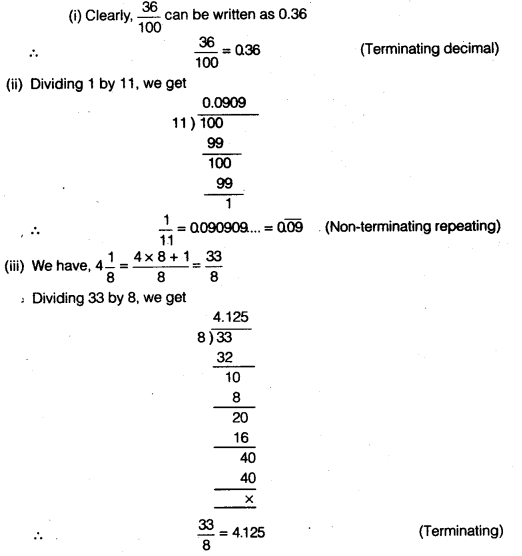
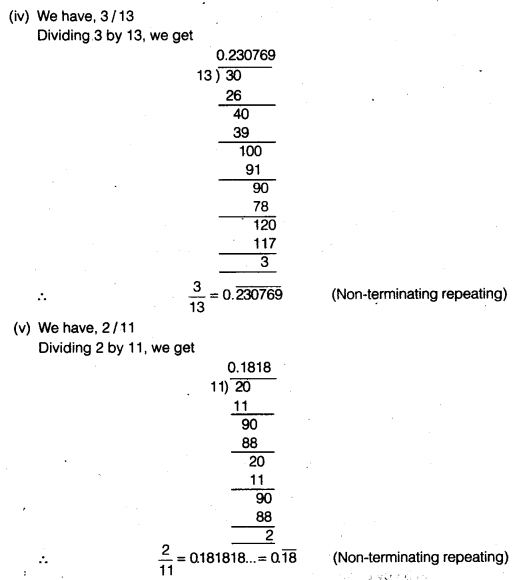

Question 2.
You know that \(\frac { 1 }{ 7 }\) = \(\bar { 0.142857 }\). Can you predict what the decimal expansions of \(\frac { 2 }{ 7 }\) , \(\frac { 13 }{ 7 }\) , \(\frac { 4 }{ 7 }\) , \(\frac { 5 }{ 7 }\) , \(\frac { 6 }{ 7 }\) are , without actually doing the long division? If so, how?
Solution:

Question 3.
Express the following in the form \(\frac { p }{ q }\)where p and q are integers and q ≠ 0.
(i) 0.\(\bar { 6 }\)
(ii) 0.4\(\bar { 7 }\)
(iii) 0.\(\overline { 001 }\)
Solution:
(i)Let x= 0.\(\bar { 6 }\) = 0.666… ….(i)
Multiplying Eq. (i) by 10, we get
10x = 6.666.. ….(ii)
On subtracting Eq. (ii) from Eq. (i), we get
(10x- x)=(6.666…) – (0.666…)
9x = 6
x= 6/9
⇒ x=2/3
(ii) Let x = 0.4\(\bar { 7 }\) = 0.4777… …(iii)
Multiplying Eq. (iii) by 10. we get
10x = 4.777… . …(iv)
Multiptying Eq. (iv) by 10, we get
100x = 47.777 ….. (v)
On subtracting Eq. (v) from Eq. (iv), we get
(100 x – 10x)=(47.777….)-(4.777…)
90x =43
⇒ x = \(\frac { 43 }{ 90 }\)
(iii) Let x = 0.\(\overline { 001 }\)= 0.001001001… …(vI)
Multiplying Eq. (vi) by (1000), we get
1000x = 1.001001001… .. .(vii)
On subtracting Eq. (vii) by Eq. (vi), we get
(1000x—x)=(1.001001001….) – (0.001001001……)
999x = 1
⇒ x = \(\frac { 1 }{ 999 }\)
Question 4.
Express 0.99999… in the form \(\frac { p }{ q }\)Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Solution:
Let x = 0.99999… ………..(i)
Multiplying Eq. (i) by 10, we get
10x = 9.99999… …(ii)
On subtracting Eq. (ii) by Eq. (i), we get
(10 x – x) = (9.99999..) – (0.99999…)
9x = 9
⇒ x = \(\frac { 9 }{ 9 }\)
x = 1
Question 5.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of \(\frac { 1 }{ 17 }\)? Perform the division to check your answer.
Solution:
The maximum number of digits in the repeating block of digits in the decimal expansion of \(\frac { 1 }{ 17 }\) is 17-1 = 16 we have,

Thus,\(\frac { 1 }{ 17 }\) = 0.\(\overline { 0588235294117647….., }\)a block of 16-digits is repeated.
Question 6.
Look at several examples of rational numbers in the form \(\frac { p }{ q }\) (q≠ 0). Where, p and q are integers with no common factors other that 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Solution:
Consider many rational numbers in the form \(\frac { p }{ q }\) (q≠ 0). where p and q are integers with no common factors other that 1 and having terminating decimal representations.
Let the various such rational numbers be \(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 4 }\), \(\frac { 5 }{ 8 }\), \(\frac { 36 }{ 25 }\), \(\frac { 7 }{ 125 }\), \(\frac { 19 }{ 20 }\), \(\frac { 29 }{ 16 }\) etc.
In all cases, we think of the natural number which when multiplied by their respective denominators gives 10 or a power of 10.
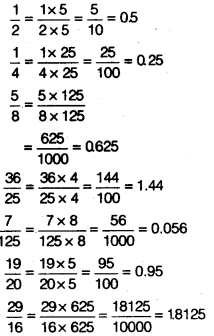
From the above, we find that the decimal expansion of above numbers are terminating. Along with we see that the denominator of above numbers are in the form 2m x 5n, where m and n are natural numbers. So, the decimal representation of rational numbers can be represented as a terminating decimal.
Question 7.
Write three numbers whose decimal expansions are non-terminating non-recurring.
Solution:
0.74074007400074000074…
0.6650665006650006650000…
0.70700700070000…
Question 8.
Find three different irrational numbers between the rational numbers \(\frac { 5 }{ 7 }\) and \(\frac { 9 }{ 11 }\) .
Solution:
To find irrational numbers, firstly we shall divide 5 by 7 and 9 by 11,
so,
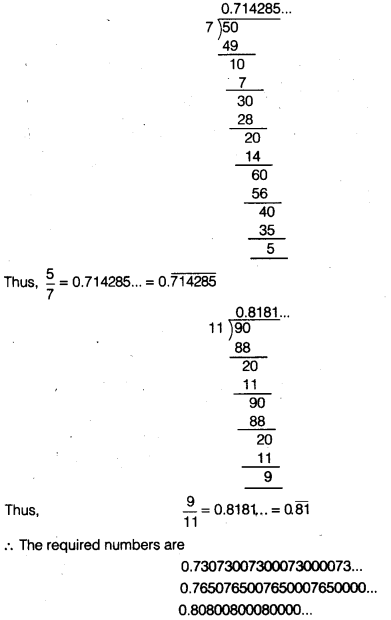
Question 9.
Classify the following numbers as rational or irrational
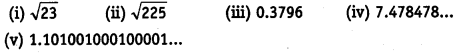
Solution:
(i) \( \sqrt{23} \) (irrational ∵ it is not a perfect square.)
(ii) \( \sqrt{225} \) = 15 (rational) (whole number.)
(iii) 0.3796 = rational (terminating.)
(iv) 7.478478… =7.\(\bar { 478 }\) = rational (non-terminating repeating.)
(v) 1.101001000100001… = irrational (non-terminating non-repeating.)
We hope the NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3, drop a comment below and we will get back to you at the earliest.