NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.2 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.2.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Chapter Name | Polynomials |
| Exercise | Ex 2.2 |
| Number of Questions Solved | 4 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.2
Question 1.
Find the value of the polynomial 5x -4x2 + 3 at
(i) x = 0
(ii) x = – 1
(iii) x = 2
Solution:
Let p (x) = 5x – 4x2+ 3
(i) The value of p (x) = 5x – 4x2+ 3 at x= 0 is
p(0) = 5 x 0 – 4 x 02+3
⇒ P (0) = 3
(ii) The value of p (x) = 5x – 4x2 + 3 at x = -1 is
p(-1) = 5(-D-4(-1)2 + 3 = – 5 -4 + 3
⇒ P(-1) = -6
(iii) The value of p (x) = 5x- 4x2 + 3 at x = 2 is
p (2) = 5 (2)- 4 (2)2 + 3= 10- 16+ 3
⇒ P (2) = – 3
Question 2.
Find p (0), p (1) and p (2) for each of the following polynomials.
(i) p(y) = y2 – y +1
(ii) p (t) = 2 +1 + 2t2 -t3
(iii) P (x) = x3
(iv) p (x) = (x-1) (x+1)
Solution:
(i) p (y) = y2 -y +1
∴ p(0) = 02-0+1
⇒ p(0) = 1
p(1) = 12-1+ 1
⇒ p(1) = 1
and p (2) = 22 – 2 + 1 =4-2+1
⇒ P (2) = 3
(ii) p (t) = 2 + t + 2t2 -13
p(0) = 2+ 0+ 2 x 02– 03
⇒ P (0) = 2
p (1) = 2 + 1 + 2 x 12 – 13
⇒ p (1) = 3 + 2 – 1
⇒ p(1) = 4
and p (2) = 2 + 2 + 2 x 22 – 23
=4+8-8
⇒ P (2) = 4
(iii) P(x) = x3
⇒ p (0) = 03 ⇒ p (0) = 0 ⇒ p (1) = 13
⇒ P (1) = 1
and p (2) = 23 ⇒ p (2) = 8
(iv) p(x) = (x-1)(x+ 1)
p(0) = (0-1)(0+1)
⇒ P (0) = – 1
p (1) = (1 – 1) (1 + 1)
⇒ P (1) = 0
and p (2) = (2-1) (2+1)
⇒ P (2) = 3
Question 3.
Verify whether the following are zeroes of the polynomial, indicated against them.
(i)p(x) = 3x + 1,x = –\(\frac { 1 }{ 3 }\)
(ii)p (x) = 5x – π, x = \(\frac { 4 }{ 5 }\)
(iii) p (x) = x2 – 1, x = x – 1
(iv) p (x) = (x + 1) (x – 2), x = – 1,2
(v) p (x) = x2, x = 0
(vi) p (x) = lx + m, x = – \(\frac { m }{ l }\)
(vii) P (x) = 3x2 – 1, x = – \(\frac { 1 }{ \sqrt { 3 } }\),\(\frac { 2 }{ \sqrt { 3 } }\)
(viii) p (x) = 2x + 1, x = \(\frac { 1 }{ 2 }\)
Solution:
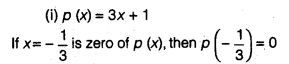
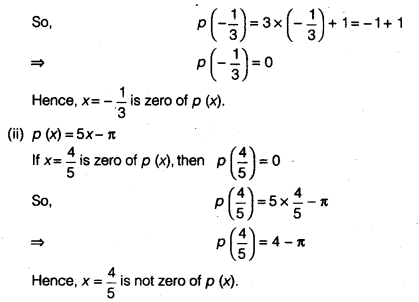
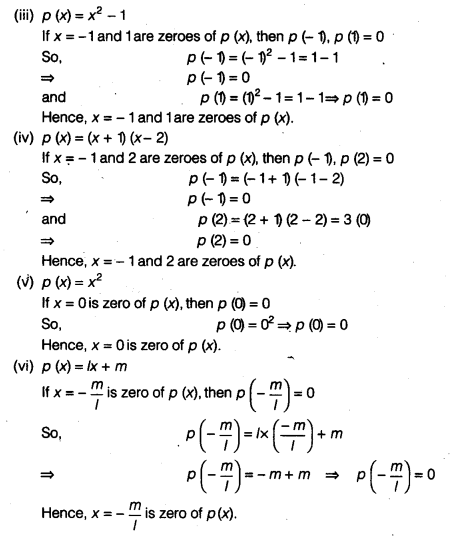

Question 4.
Find the zero of the polynomial in each of the following cases
(i) p(x)=x+5
(ii) p (x) = x – 5
(iii) p (x) = 2x + 5
(iv) p (x) = 3x – 2
(v) p (x) = 3x
(vi) p (x)= ax, a≠0
(vii) p (x) = cx + d, c≠ 0 where c and d are real numbers.
Solution:
(i) We have, p (x)= x+ 5
Now, p (x) = 0
⇒ x+ 5 = 0
⇒ x = -5
∴ – 5 is a zero of the polynomial p (x).
(ii) We have, p (x) = x – 5
Now, p (x) = 0
⇒ x – 5 = 0
⇒ x = 5
∴ 5 is a zero of the polynomial p (x).
(iii) We have, p (x) = 2x + 5
Now, P (x)= 0
⇒ 2x+ 5= 0
⇒ x = –\(\frac { 5 }{ 2 }\)
∴ –\(\frac { 5 }{ 2 }\) is a zero of the polynomial p (x).
(iv) We have, p (x)= 3x- 2
Now p(x) = 0
⇒ 3x- 2 = 0
⇒ x= \(\frac { 2 }{ 3 }\)
∴ \(\frac { 2 }{ 3 }\) is a zero of the polynomial p (x).
(v) We have, p (x) = 3x
Now, p (x)= 0
⇒ 3x=0
⇒ x =0
∴ 0 is a zero of the polynomial p (x).
(vi) We have, p (x)= ax, a ≠ 0
Now, p (x)= 0 ⇒ ax= 0
⇒ x= 0
∴ 0 is.a zero of the polynomial p (x).
(vii) We have, p (x) = cx + d,c ≠ 0
Now, p (x) = 0
⇒ cx + d = 0
x = – \(\frac { d }{ c }\)
∴ – \(\frac { d }{ c }\) is a zero of the polynomial p (x).
We hope the NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.2, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.2, drop a comment below and we will get back to you at the earliest.