NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 9 |
| Chapter Name | Quadrilaterals |
| Exercise | Ex 9.2 |
| Number of Questions Solved | 7 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2
Question 1.
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see figure). AC is a diagonal. Show that
(i) SR || AC and SR = \(\frac { 1 }{ 2 }\) AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
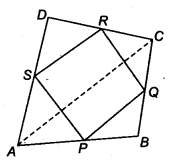
Solution:
Given: P, Q, Ft and S are mid-points of the sides.
∴ AP = PB, BQ = CQ
CR = DR and AS = DS
(i) In ∆ADC, we have
S is mid-point of AD and R is mid-point of the DC.
We know that, the line segment joining the mid-points of two sides of a triangle is parallel to the third side.
∴ SB || AC …(i)
Also , SR = \(\frac { 1 }{ 2 }\) AC …(ii)
(ii) Similarly, in ∆ABC, we have
PQ || AC ….(iii)
and PQ = \(\frac { 1 }{ 2 }\) AC ….(iv)
Now, from Eqs. (i) and (iii), we get
SR = \(\frac { 1 }{ 2 }\) AC …..(v)
(iii) Now, from Eqs. (i) and (iii), we get
PQ || SR
and from Eq. (v), PQ = SR
Since, a pair of opposite sides of a quadrilateral PQRS is equal and parallel.
So, PQRS is a parallelogram.
Hence proved.
Question 2.
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
Given: ABCD is a rhombus and P, Q, R and S are mid-points of AB, BC, CD and DA
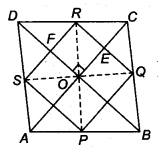
By mid-point theorem,

∴ PQRS is a parallelogram.
Now, we know that diagonals of a rhombus bisect each other at right angles.
∴ ∠EOF = 90°
Now, RQ || BD (By mid-point theorem)
⇒ RE || OF
Also, SP|| AC [From Eq. (i)]
⇒ FR || OE
∴ OERF is a parallelogram.
So, ∠ ERF = ∠EOF = 90°
(Opposite angle of a quadrilateral is equal)
Thus, PQRS is a parallelogram with ∠R = 90°
Hence, PQRS is a rectangle.
Question 3.
ABCD is a rectangle and P, Q, R ans S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
Given: ABCD is a rectangle.
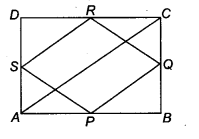
∴ ∠A = ∠B = ∠C= ∠D = 90°
and AD = BC, AB = CD
Also, given P, Q, R and S are mid-points of AB, BC, CD and DA .respectively.
∴ PQ || BD and PQ = \(\frac { 1 }{ 2 }\) BD
In rectangle ABCD,
AC = BD
∴ PQ = SR …(ii)
Now, in ∆ASP and ∆BQP
AP = BP (Given)
AS = BQ (Given)
∠A = ∠B (Given)
∴ ∆ASP ≅ ∆BQP (By SAS)
∴ SP = PQ (By CPCT)…(ii)
Similarly, in ∆RDS and ∆RCQ,
SD = CQ (Given)
DR = RC (Given)
∠C=∠D (Given)
∴ ∆RDS ≅ ∆RCQ (By SAS)
∴ SR = RQ (By CPCT)…(iii)
From Eqs. (i), (ii) and (iii), it is clear that quadrilateral PQRS is a rhombus.
Question 4.
ABCD is a trapezium in which AB | | DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see figure). Show that F is the mid-point of BC.
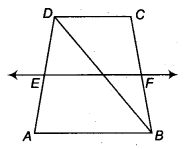
Solution:
Given: ABCD is a trapezium in which AB || CD and E is mid-point of AD and EF || AB.
In ∆ABD, we have
EP\\AB
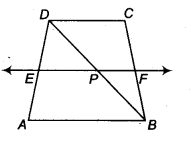
and E is mid-point of AD.
So, by theorem, if a line drawn through the mid-point of one side of a triangle parallel to another side bisect the third side.
∴ P is mid-point of BD.
Similarly, in ∆ BCD, we have,
PF || CD (Given)
and P is mid-point of BD.
So, by converse of mid-point theorem, F is mid-point of CB.
Question 5.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see figure). Show that the line segments AF and EC trisect the diagonal BD.
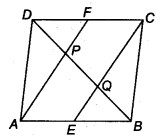
Solution:
Given: ABCD is a parallelogram and E, F are the mid-points of sides AB and CD respectively.
To prove: Line segments AF and EC trisect the diagonal BD.
Proof: Since, ABCD is a parallelogram.
AB || DC
and AB = DC (Opposite sides of a parallelogram)
⇒ AE || FC and \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) DC
⇒ AF || FC and AF = FC
∴ AECF is a parallelogram.
∴ AF || FC
⇒ EQ || AP and FP || CQ
In ∆ BAP, E is the mid-point of AB and EQ || AP, so Q is the mid-point of BP.
(By converse of mid-point theorem)
∴ BQ = PQ ….(i)
Again, in ∆DQC, F is the mid-point of DC and FP || CQ, so P is the mid-point of DQ. (By converse of mid-point theorem)
∴ QP = DP …(ii)
From Eqs. (i) and (ii), we get
BQ = PQ = PD
Hence, CE and AF trisect the diagonal BD.
Question 6.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:
Let ABCD is a quadrilateral and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively, i.e., AS = SD, AP = BP, BQ = CQ and CR = DR. We have to show that PR and SQ bisect each other i.e., SO = OQ and PO = OR.
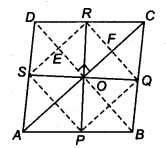
Now, in ∆ADC, S and R are mid-points of AD and CD.
We know that, the line segment joining the mid-points of two sides of a triangle is parallel to the third side. (By mid-point theorem)
∴ SR || AC and SR = \(\frac { 1 }{ 2 }\) AC …(i)
Similarly, in ∆ ABC, P and Q are mid-points of AB and BC.
∴ PQ || AC and PQ = \(\frac { 1 }{ 2 }\) AC (By mid-point theorem)…(ii)
From Eqs. (i) and (ii), we get
PQ || SR
and PQ = SR = \(\frac { 1 }{ 2 }\) AC
∴ Quadrilateral PQRS is a parallelogram whose diagonals are SQ and PR. Also, we know that diagonals of a parallelogram bisect each other. So, SQ and PR bisect each other.
Question 7.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac { 1 }{ 2 }\) AB
Solution:
Given: ABC is a right angled triangle.
∠C = 90°
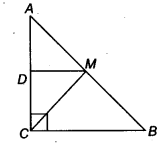
and M is the mid-point of AB.
Also, DM || BC
(i) In ∆ ABC, BC || MD and M is mid-point of AB.
∴ D is the mid-point of AC. (By converse of mid-point theorem)
(ii) Since, MD || BC and CD is transversal
∴ ∠ADM = ∠ACB (Corresponding angles)
But ∠ACB = 90°
∴ ∠ADM = 90° ⇒ MD ⊥ AC
(iii) Now, in ∆ ADM and ∆ CDM, we have
DM = MD (Common)
AD = CD (∵ D is mid point of AC)
∴ ∠ADM = ∠MDC (Each equal to 90°)
∴ ∆ ADM = ∆ CDM (By SAS)
∴ CM = AM (By CPCT)…(i)
Also, M is mid-point of AB.
∴ AM – BM = \(\frac { 1 }{ 2 }\) AB ….(ii)
From Eqs. (i) and (ii), we get
CM = AM = \(\frac { 1 }{ 2 }\) AB
Hence proved.
We hope the NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 9 Quadrilaterals Ex 9.2, drop a comment below and we will get back to you at the earliest.