Here we are providing Polynomials Class 10 Extra Questions Maths Chapter 2 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/
Extra Questions for Class 10 Maths Polynomials with Answers Solutions
Extra Questions for Class 10 Maths Chapter 2 Polynomials with Solutions Answers
Polynomials Class 10 Extra Questions Very Short Answer Type
The graphs of y = p(x) for some polynomials (for questions 1 to 4) are given below. Find the number of zeros in each case.
Polynomials Class 10 Extra Questions Question 1.
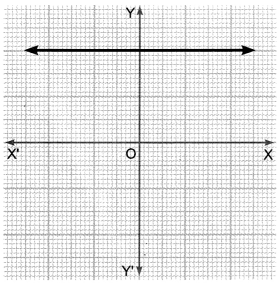
Answer:
There is no zero as the graph does not intersect the X-axis.
Polynomial Class 10 Extra Questions Question 2.
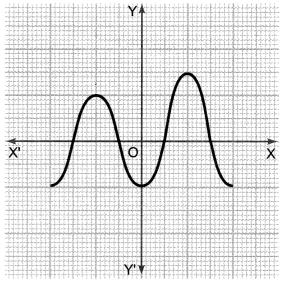
Answer:
The number of zeros is four as the graph intersects the X-axis at four points.
Polynomials Class 10 Extra Questions With Answers Question 3.
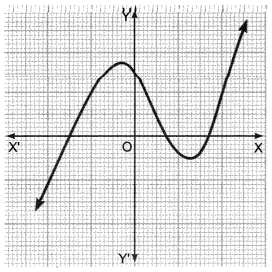
Answer:
The number of zeros is three as the graph intersects the X-axis at three points.
Class 10 Polynomials Extra Questions Question 4.
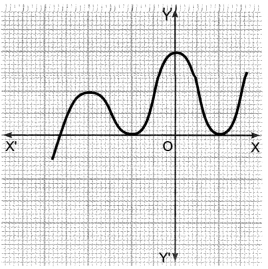
Answer:
The number of zeros is three as the graph intersects the X-axis at three points.
Class 10 Maths Chapter 2 Extra Questions Question 5.
What will the quotient and remainder be on division of ax2 + bx + c by px2 + qx2 + rx + 5, p ≠ 0?
Answer:
0, ax2 + bx + C.
Polynomials Class 10 Questions With Answers Question 6.
If on division of a polynomial p(x) by a polynomial g(x), the quotient is zero, what is the relation between the degrees of p(x) and g(x)?
Answer:
Since the quotient is zero, therefore
deg p(x) < deg g(x)
Polynomials Extra Questions Class 10 Question 7.
Can x – 2 be the remainder on division of a polynomial p(x) by x + 3?
Answer:
No, as degree (x – 2) = degree (x + 3)
Extra Questions Of Polynomials Class 10 Question 8.
Find the quadratic polynomial whose zeros are -3 and 4.
[NCERT Exemplar]
Answer:
Sum of zeros = -3 + 4 = 1,
Product of zeros = – 3 x 4 = -12
∴ Required polynomial = x2 – x – 12
Extra Questions On Polynomials Class 10 Question 9.
If one zero of the quadratic polynomial x2 – 5x – 6 is 6 then find the other zero.
Answer:
Let α,6 be the zeros of given polynomial.
Then α + 6 = 5 3 ⇒ α = -1
Extra Questions For Class 10 Maths Chapter 2 Question 10.
If both the zeros of the quadratic polynomial ax2 + bx + c are equal and opposite in sign, then find the value of b.
Answer:
Let α and -α be the roots of given polynomial.
Then α + (-α) = 0 ⇒ \(-\frac{b}{a}=0\) ⇒ b = 0.
Polynomial Extra Questions Class 10 Question 11.
What number should be added to the polynomial x2 – 5x + 4, so that 3 is the zero of the polynomial?
Answer:
Let f(x) = x2 – 5x + 4
Then f(3) = 32 – 5 x 3 + 4 = -2
For f(3) = 0, 2 must be added to f(x).
Polynomials Extra Questions Question 12.
Can a quadratic polynomial x2 + kx + k have equal zeros for some odd integer k > 1?
Answer:
No, for equal zeros, k = 0,4 ⇒ k should be even.
Class 10 Maths Polynomials Extra Questions Question 13.
If the zeros of a quadratic polynomial ax2 + bx + c are both negative, then can we say a, b and c all have the same sign? Justify your answer.
Answer:
Yes, because \(-\frac{b}{a}\) = sum of zeros < 0, so that \(\frac{b}{a}=0\) > 0. Also the product of the zeros = \(\frac{c}{a}=0\) > 0.
Chapter 2 Maths Class 10 Extra Questions Question 14.
If the graph of a polynomial intersects the x-axis at only one point, can it be a quadratic polynomial?
Answer:
Yes, because every quadratic polynomial has at the most two zeros.
Extra Questions Of Polynomials Class 10 With Solutions Question 15.
If the graph of a polynomial intersects the x-axis at exactly two points, is it necessarily a quadratic polynomial?
Answer:
No, x4 – 1 is a polynomial intersecting the x-axis at exactly two points.
Polynomials Class 10 Extra Questions Short Answer Type 1
Question 1.
If one of the zeros of the quadratic polynomial f(x) = 4x2 – 8kx – 9 is equal in magnitude but opposite in sign of the other, find the value of k.
Answer:
Let one root of the given polynomial be α.
Then the other root = -α
Sum of the roots = (-α) + α = 0
⇒ \(-\frac{b}{a}\) = 0 or \(-\frac{8k}{4}\) = 0 or k = 0
Question 2.
If one of the zeros of the quadratic polynomial (k – 1)x2 + kx + 1 is -3 then find the value of k.
Answer:
Since – 3 is a zero of the given polynomial
∴ (k – 1)(-3)2 + k(-3) + 1 = 0 :
⇒ 9k – 9 – 3k + 1 = 0 ⇒ k = 4/3.
Question 3.
If 1 is a zero of the polynomial p(x) = ax2 – 3(a – 1)x -1, then find the value of a.
Answer:
Put x = 1 in p(x)
∴ p(1) = a(1)2 – 3(a – 1) x 1 – 1 = 0
⇒ a – 3a + 3 – 1 = 0 ⇒ 2a = -2 ⇒ a = 1
Question 4.
If α and β are zeros of polynomial p(x) = x2 – 5x + 6, then find the value of α + B – 3aß.
Answer:
Here, α + β = 5, αβ = 6
= α + β – 3αβ = 5 – 3 x 6 = -13
Question 5.
Find the zeros of the polynomial p(x) = 4x2 – 12x + 9.
Answer:
p(x) = 4x2 – 12x + 9 = (2x – 3)2
For zeros, p(x) = 0
⇒ (2x – 3)(2x – 3) = 0 ⇒ x = \(\frac{3}{2}, \frac{3}{2}\)
Question 6.
If one root of the polynomial p(y) = 5y2 + 13y + m is reciprocal of other, then find the value of m.
Answer:
![]()
Question 7.
If α and β are zeros of p(x) = x2 + x – 1, then find \(\frac{1}{\alpha}+\frac{1}{\beta}\)
Answer:
Here, α + β = -1, αβ = -1,
So \(\frac{1}{\alpha}+\frac{1}{\beta}=\frac{\beta+\alpha}{\alpha \beta}=\frac{-1}{-1}=1\)
Question 8.
Given that one of the zeros of the cubic polynomial ax3 + bx2 + cx + d is zero, find the product of the other two zeros.
Answer:
Let α, β, γ be the roots of the given polynomial and α = 0.
Then αβ + βγ + γα = c/a ⇒ βγ = c/a
Question 9.
If the product of two zeros of the polynomial p(x) = 2x3 + 6x2 – 4x + 9 is 3, then find its third zero.
Answer:
Let α, β, γ be the roots of the given polynomial and αβ = 3
Then αβγ = \(-\frac{9}{2}\)
⇒ 3 x γ = \(\frac{-9}{2}\) or γ = \(\frac{-3}{2}\)
Question 10.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeros respectively.
(i) \(-\frac{1}{4}, \frac{1}{4}\)
(ii) \(\sqrt{2}, \frac{1}{3}\)
Answer:
Let α, β be the zeros of polynomial.
(i) We have, α + β = \(-\frac{1}{4}\) and αβ = \(\frac{1}{4}\)
Thus, polynomial is
p(x) = x2 – (a + B) x + aß

Quadratic polynomial 4x2 + x + 1
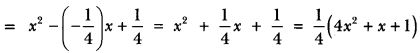
(ii) We have, α + β = √2 and αβ = \(\frac{1}{3}\)
Thus, polynomial is p(x) = x2 – (α + β) x + αβ
= x2 – √2x + \(\frac{1}{3}\) = \(\frac{1}{3}\) (3x2 – 3√2x + 1)
Quadratic polynomial = 3x2 – 3√2x + 1
Polynomials Class 10 Extra Questions Short Answer Type 2
Find the zeros of the following quadratic polynomials and verify the relationship between the zeros and the coefficients (Q. 1 – 2).
Question 1.
6x2 – 3 – 7x
Answer:
We have, p(x) = 6x2 – 3 – 7x
p(x) = 6x2 – 7x – 3
(In general form)
= 6x2 – 9x + 2x – 3 = 3x (2x – 3) + 1 (2x – 3)
= (2x – 3) (3x + 1)
The zeros of polynomial p(x) is given by
p(x) = 0) = (2x – 3) (3x + 1) = 0 ⇒ \(x=\frac{3}{2},-\frac{1}{3}\)
Thus, the zeros of 6x2 – 7x – 3 are α = \(-\frac{3}{2}\) and β = \(-\frac{1}{3}\)
Now, sum of the zeros = α + β = \(\frac{3}{2}-\frac{1}{3}\) = \(\frac{9-2}{6}=\frac{7}{6}\)

Question 2.
4u2 + 8u
Answer:
We have, p(u) = 4u2 + 8u = p(u) = 4u (u + 2)
The zeros of polynomial p(u) is given by
p(u) = 0 ⇒ 4u (u + 2) = 0 .
∴ u = 0, -2
Thus, the zeros of 4u2 + 8u are α = 0 and β = -2
Now, sum of the zeros = α + β = 0 – 2 = -2

Question 3.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2 (ii) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
Answer:
(i) We have,
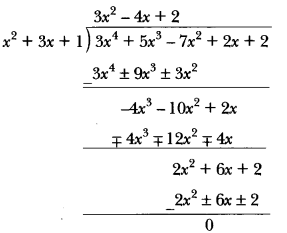
Clearly, remainder is zero, so x2 + 3x + 1 is a factor of polynomial 3x4 + 5x3 – 7x2 + 2x + 2
(ii) We have,

Clearly, remainder is zero, so t’ – 3 is a factor of polynomial 2t4 + 3t3 – 2t2 – 9t – 12.
Question 4.
If α and β are the zeros of the quadratic polynomial f(x) = 2x2 – 5x + 7, find a polynomial whose zeros are 2α + 3β and 3α + 2β.
Answer:
Since α and β are the zeros of the quadratic polynomial f(x) = 2x2 – 5x + 7
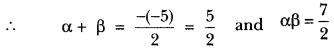
Let S and P denote respectively the sum and product of the zeros of the required polynomial.
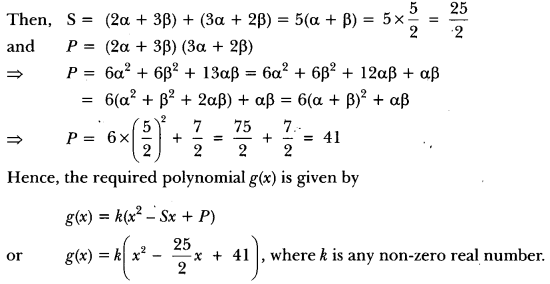
Question 5.
What must be subtracted from p(x) = 8x4 + 14x3 – 2x2 + 7x – 8 so that the resulting polynomial
is exactly divisible by g(x) = 4x2 + 3x – 2?
Answer:
Let y be subtracted from polynomial p(x)
: 8x4 + 14x3 – 2x2 + 7x – 8 – y is exactly divisible by g(x)
Now,
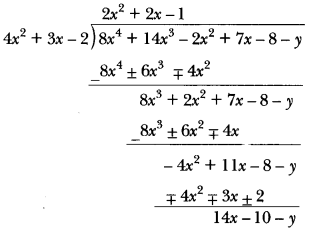
∵ Remainder should be 0.
∴ 14x – 10 – y = 0 or 14x – 10 = y or y = 14x – 10
∴ (14x – 10) should be subtracted from p(x) so that it will be exactly divisible by g(x)
Question 6.
What must be added to f(x) = 4x4 + 2x3 – 2x2 + x – 1 so that the resulting polynomial is divisible
by g(x) = x2 + 2x – 3?
Answer:
By division algorithm, we have
f(x) = g(x) × q(x) + r(x)
= f(x) – r(x) = g(x) × q(x) ⇒ f(x) + {-r(x)} = g(x) × q(x)
Clearly, RHS is divisible by g(x). Therefore, LHS is also divisible by g(x). Thus, if we add –r(x) to f(x), then the resulting polynomial is divisible by g(x). Let us now find the remainder when f(x) is divided by g(x).
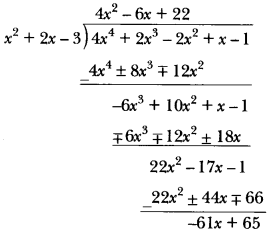
∴ r(x) = -61x + 65 or -r(x) = 61x – 65
Hence, we should add –r(x) = 61x – 65 to f(x) so that the resulting polynomial is divisible by g(x).
Question 7.
Obtain the zeros of quadratic polynomial 3x2 – 8x + 4√3 and verify the relation between its zeros and coefficients.
Answer:
We have,
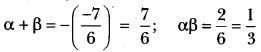
Question 8.
If α and β are the zeros of the polynomial 6y2 – 7y + 2, find a quadratic polynomial whose zeros are \(\frac{1}{\alpha}\) and \(\frac{1}{\beta}\)
Answer:
Let p(y) = 6y2 – 7y + 2
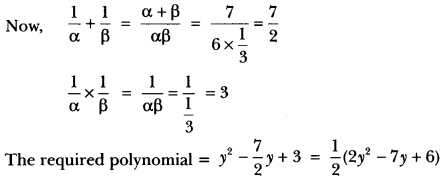
Question 9.
If one zero of the polynomial 3x2 – 8x + 2k + 1 is seven times the other, find the value of k.
Answer:
Let α and β be the zeros of the polynomial. Then as per question β = 7α
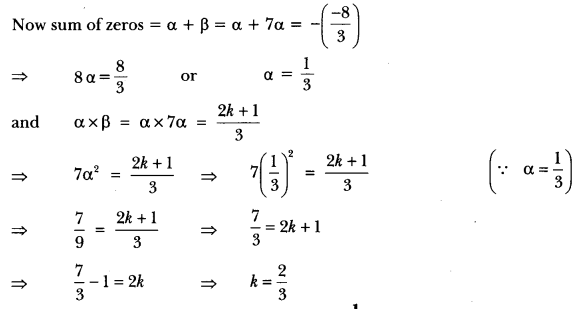
Question 10.
If one zero of the polynomial 2x2 + 3x + λ is 1/2 find the value of and other zero.
Answer:
Let P(x) = 2x2 + 3x + λ
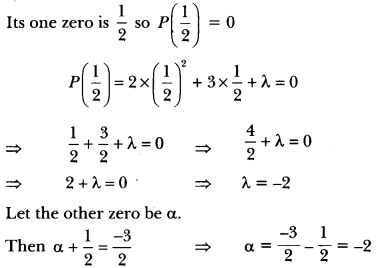
Question 11.
If one zero of polynomial (a2 + 9)x2 + 13x + 6a is reciprocal of the other, find the value of a.
Answer:
Let one zero of the given polynomial be α.
Then, the other zero is 1/α
∴ Product of zeros = α × \(\frac{1}{\alpha}\) = 1
But, as per the given polynomial product of zeros = \(\frac{6 a}{a^{2}+9}\)
∴ \(\frac{6 a}{a^{2}+9}\) = 1 ⇒ a2 + 9 = 6a
⇒ a2 – 6a + 9 = 0) ⇒ (a – 3)2 = 0
⇒ a – 3 = 0 ⇒ a = 3
Hence, a = 3.
Question 12.
If the polynomial (x4 + 2x3 + 8x2 + 12x + 18) is divided by another polynomial (x2 + 5), the remainder comes out to be (px +q). Find values of p and q.
Answer:
Let f(x) = (x4 + 2x3 + 8x2 + 12x + 18) and g(x) = (x2 + 5)
On dividing f(x) by g(x), we get
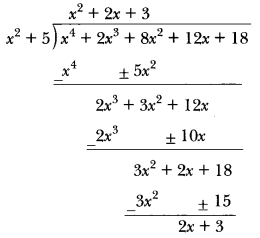
Now, px + 9 = 2x + 3 ⇒ p = 2,q = 3 (By comparing the coefficient of x and constant term).
Polynomials Class 10 Extra Questions Long Answer Type 1
Question 1.
Verify that the numbers given alongside the cubic polynomial below are their zeros. Also verify the relationship between the zeros and the coefficients.
x3 – 4x2 + 5x – 2; 2,1,1
Solution:
Let p(x) = x3 – 4 x2 + 5x – 2
On comparing with general polynomial px) ax3 + bx2 + cx + d, we get a = 1, b = -4, c = 5 and d = -2
Given zeros 2, 1, 1.
∴ p(2) = (2)3 – 4(2)2 + 5(2) – 2 = 8 – 16 + 10 – 2 = 0
and p(1) = (1)3 – 4(1)2 + 5(1) – 2 = 1 – 4 + 5 – 2 = 0
Hence, 2, 1 and I are the zeros of the given cubic polynomial.
Again, consider α = 2, β = 1, γ = 1
∴ α + 13 + y = 2 + 1 + 1 = 4

Question 2.
Find a cubic polynomial with the sum of the zeros, sum of the products of its zeros taken two at a time, and the product of its zeros as 2, -7, -14 respectively.
Solution:
Let the cubic polynomial be p(x) = ax3 + bx2 + cx + d. Then
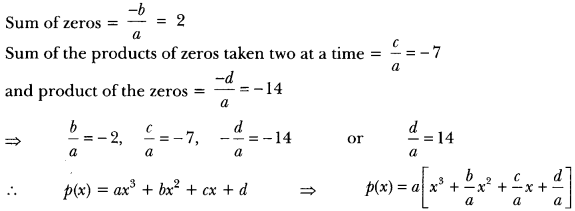
p(x) = a[x3 + (-2)x2 + (-7)x + 14] ⇒ p(x) = a[x3 – 2x2 – 7x + 14]
For real value of a = 1, p(x) = x3 – 2x2 – 7x + 14
Question 3.
Find the zeros of the polynomial f(x) = x3 – 5x2 – 2x + 24, if it is given that the product of its two zeros is 12.
Solution:
Let α, β and γ be the zeros of polynomial (fx) such that αβ = 12.
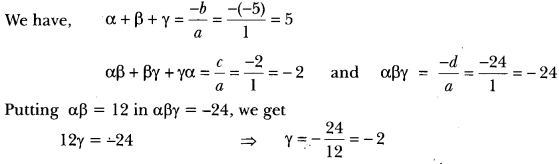
Now, α + β + γ = 5 α + β – 2 = 5
= α + β = 7 a = 7 – β
= (7 – β) β =12 ⇒ 7β – β2 – 12
= β2 + 7β + 12 = 0 ⇒ β2 – 3β – 4β + 12 = O
= β = 4 or β = 3
β = 4 or β = 3
∴ α = 3 or α = 4
Question 4.
If the remainder on division of x3 – kx2 + 13x – 21 by 2x – 1 is -21, find the quotient and the value of k. Hence, find the zeros of the cubic poIyncmia1 x3 – kx2 + 13x.
Solution:
Let f(x) = x3 – kx2 + 13x – 21
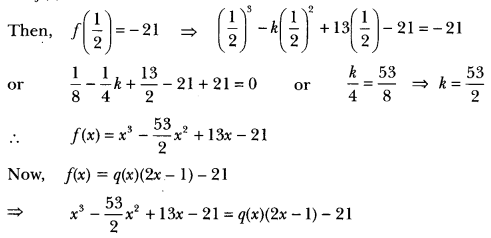

Question 5.
Obtain all other zeros of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeros are \(\sqrt{\frac{5}{3}}\) and \(\sqrt{\frac{5}{3}}\).
Solution:
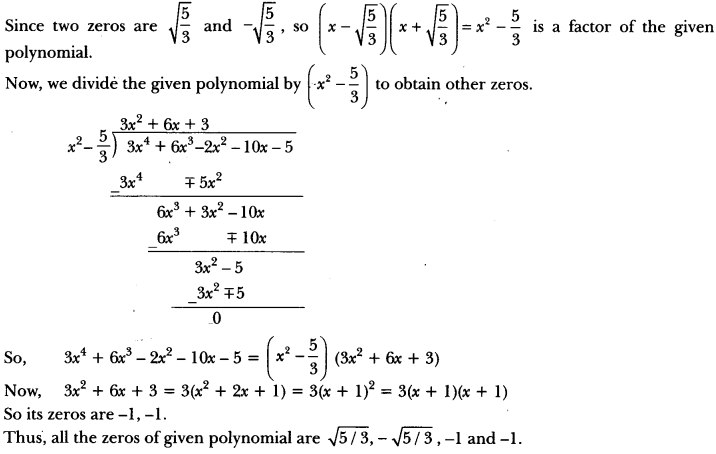
Question 6.
Given that √2 is a zero of the cubic polynomial 6x3 + √2x2 – 10x – 4√2, find its other zeros.
Solution:
The given polynomial is f(x) = (6x3 +√2x2 – 10x – 4√2). Since √2 is the zero of f(x), it follows that (x – √2) is a factor of f(x).
On dividing f(x) by (x – √2), we get
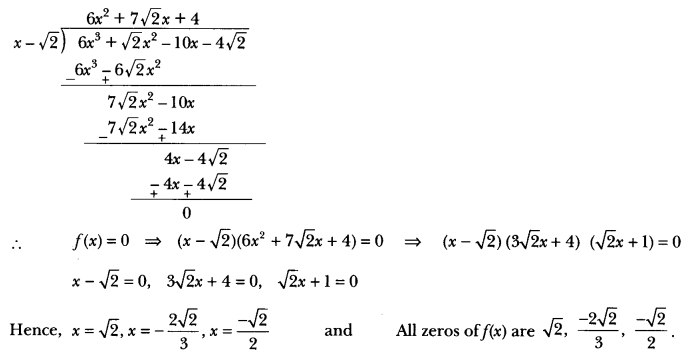
Polynomials Class 10 Extra Questions HOTS
Question 1.
If α, β, γ bezerosofpo1ynomia1 6x3 + 3x2 – 5x + 1, then find die value of α-1 + β-1 + γ-1.
Solution:
∵ p(x) = 6x3 + 3x2 – 5x + 1 so a = 6, b = 3, c = -5, d = 1
∴ α, β and γ are zeros of the polynomial p(x).
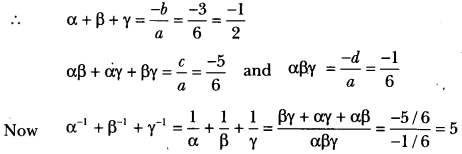
Question 2.
Find the zeros of the polynomial f(x) = – 12x2 + 39x – 28, if it is given that the zeros are in AP.
Solution:
If α, β, γ are in AP., then,
β – α = γ + β ⇒ 2β = α + γ
α + β + γ = \(\frac{-b}{a}\) = \(\frac{-(-12)}{1}\) = 12 ⇒ α + γ = 12 – β …….. (i)
From (i) and (ii)
2β = 12 – β or 3β = 12 or β = 4
Putting the value of β in (i), we have
8 = a + γ
αβγ = – \(\frac{d}{a}\) = \(\frac{-(-28)}{1}\) = 28 …….. (iii)
(αγ) 4 = 28 or αγ = 7 or γ = \(\frac{7}{α}\) ….. (iv)
Putting the value of γ = \(\frac{7}{α}\) in (iii), we get
⇒ 8 = α + \(\frac{7}{α}\) ⇒ 8α = α2 + 7
⇒ α2 – 8α + 7 = 0 ⇒ α2 – 7α – 1α + 7 = 0
⇒ α(α – 7)-1 (α – 7) = 0 ⇒ (α – 1)(α – 7) = 0
⇒ α = 1 or α = 7

Question 3.
If the polynomial f(x) = x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a. Find k and a.
Solution:
By division algorithm, we have Dividend = Divisor × Quotient + Remainder
⇒ Dividend – Remainder = Divisor × Quotient
⇒ Dividend – Remainder is always divisible by the divisor.
When f(x) = – 6x3 + 16x2 – 25x + 10 is divided by x2 – 2x + k the remainder comes out to be x + a.
∴ f(x) – (x + a) = x4 – 6x3+ 16x2 – 25x + 10 – (x + a)
= x4 – 6x3 + 16x2 – 25x + 10 – x – a x4 – 6x3 + 16x2 – 26x + 10 – a
is exactly divisible by x2 – 2x + k
Let us now divide x4 – 6x3 + 16x2 – 26x + 10 – a by x2 – 2x + k.
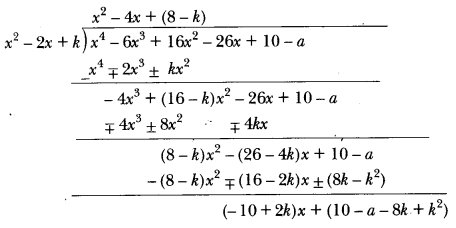
For f(x) – (x + a) = x4 – 6x3 + 16x2 – 26x + 10 – a to be exactly divisible by x2 – 2x + k, we must
have (-10 + 2k)x + (10 – a – 8k + k2) = 0 for all x
= – 10 + 2k = 0 and 10 – a – 8k + k2 = 0
⇒ k = 5 and 10 – a – 40 + 25 = 0
⇒ k = 5 and a – 5
