Here we are providing Probability Class 10 Extra Questions Maths Chapter 15 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/
Extra Questions for Class 10 Maths Probability with Answers Solutions
Extra Questions for Class 10 Maths Chapter 15 Probability with Solutions Answers
Probability Class 10 Extra Questions Very Short Answer Type
Probability Class 10 Extra Questions Question 1.
State true or false and give the reason. If I toss a coin 3 times and get head each tir ne, then I should expect a tail to have a higher chance in the 4th toss.
Solution:
False, because the outcomes ‘head’ and ‘tail are equally likely. So, every time the probability of getting head or tail is \(\frac{1}{2}\)
Class 10 Probability Extra Questions Question 2.
A bag contains slips numbered from 1 to 100. If Fatima chooses a slip at random from the bag, it will either be an odd number or an even number. Since, this situation has only two possible outcomes, so the probability of each is \(\frac{1}{2}\) Justify.
Solution:
True, because the outcomes odd number’ and `even number’ are equally likely here.
Probability Class 10 Extra Questions With Answers Pdf Question 3.
In a family, having three children, there may be no girl, one girl, two girls or three girls. So, the probability of each is \(\frac{1}{4}\). Is this correct? Justify your answer.
Solution:
False, because the outcomes are not equally, likely. For no girl, outcome is bbb, for one girl, it is
bgb, gbb, bbg, for two girls, it is bgg, ggb, gbg and for all girls, it is ggg.
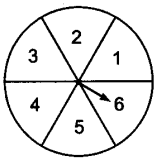
Probability Extra Questions Class 10 Question 4.
A game consists of spinning an arrow which comes to rest pointing at one of the regions (1, 2 or 3) (Fig. 15.1). Are the outcomes 1, 2 and 3 equally likely to occur? Give reason.
Solution:
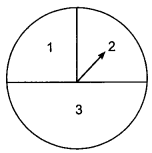
False, because the outcome 3 is more likely than the other numbers.
Extra Questions Of Probability Class 10 Question 5.
Two coins are tossed simultaneously. Find the probability of getting exactly one head.
Solution:
Possible outcomes are {HH, HT, TH, TT}.
(exactly one head) = \(\frac{2}{4}\) = \(\frac{1}{2}\)
Extra Questions On Probability Class 10 Question 6.
From a well shuffled pack of cards, a card is drawn at random. Find the probability of getting a black queen.
Solution:
Number of black queens in a pack of cards = 2
∴ P (black queen) = \(\frac{2}{52}\) = \(\frac{1}{26}\)
Probability Extra Questions Question 7.
If P (E) = 0.05, what is the probability of ‘not E’ ?
Solution:
As we know that,
P (E) + P (not E) = 1
P (not E) = 1 – P (E) = 1 – 0.05 = 0.95
Probability Class 10 Extra Questions With Solutions Question 8.
What is the probability of getting no head when two coins are tossed simultaneously?
Solution:
Favourable outcome is TT;
∴ P (no head) = \(\frac{1}{4}\)
Class 10 Maths Probability Extra Questions Question 9.
In a single throw of a pair of dice, what is the probability of getting the sum a perfect square?
Solution:
Total outcomes = 36
Favourable outcomes are {(1,3), (3, 1), (2, 2), (3, 6), (6,3), (4, 5), (5, 4)}
∴ Required probability = \(\frac{7}{36}\)
Probability Class 10 Important Questions Question 10.
Someone is asked to choose a number from 1 to 100. What is the probability of it being a prime number?
Solution:
Total prime numbers between 1 to 100 = 25
∴ P (Prime number) = \(\frac{25}{100}\) = \(\frac{1}{4}\)
Extra Sums Of Probability Class 10 Question 11.
Cards marked with number 3, 4, 5, …., 50 are placed in a box and mixed thoroughly. A card is drawn at random from the box. Find the probability that the selected card bears a perfect square number.
Solution:
Possible outcomes are 4, 9, 16, 25, 36, 49, i.e., 6.
∴ P (perfect square number) = \(\frac{6}{48}\) or \(\frac{1}{8}\)
Probability Questions Class 10 Question 12.
A card is drawn at random from a well shuffled pack of 52 playing cards. Find the probability of getting neither a red card nor a queen.
Solution:
Number of possible outcomes = 52
Number of red cards and queens = 28
Number of favourable outcomes = 52 – 28 = 24
P (getting neither a red card nor a queen) = \(\frac{24}{52}\) = \(\frac{6}{13}\)
Questions On Probability Class 10 Question 13.
20 tickets, on which numbers 1 to 20 are written, are mixed throughly and then a ticket is drawn at random out of them. Find the probability that the number on the drawn ticket is a multiple of 3 or 7.
Solution:
n(s) = 20, Multiples of 3 or 7, A: {3, 6, 9, 12, 15, 18, 7, 14), n(A) = 8
∴ Required probability = \(\frac{8}{20}\) or \(\frac{2}{5}\)
Probability Important Questions Class 10 Question 14.
A number is chosen at random from the numbers -3, -2, -1, 0, 1, 2, 3. What will be the probability that square of this number is less then or equal to 1?
Solution:
Favourable outcomes are -1, 0, 1 = 3
Total outcomes = 7
∴ Required probability = \(\frac{3}{7}\)
Probability Class 10 Extra Questions Short Answer Type 1
Class 10 Maths Ch 15 Extra Questions Question 1.
Two dice are thrown at the same time and the product of numbers appearing on them is noted. Find the probability that the product is a prime number.
Solution:
Product of the number on the dice is prime number, i.e., 2, 3, 5.
The possible ways are, (1, 2), (2, 1), (1, 3), (3, 1), (5, 1), (1, 5)
So, number of possible ways = 6
∴ Required probability = \(\frac{6}{36}\) = \(\frac{1}{6}\)
Class 10th Probability Extra Questions Question 2.
Find the probability that a number selected from the numbers 1 to 25 is not a prime number when each of the given numbers is equally likely to be selected.
Solution:
Total prime numbers from 1 to 25 = 9.
∴ Non-prime numbers from 1 to 25 = 25 – 9 = 16.
⇒ P (non-prime number) = \(\frac{16}{25}\)
Probability Class 10 Important Questions 2020 Question 3.
One card is drawn at random from a pack of 52 cards. Find the probability that the card drawn is an ace and black.
Solution:
Number of black aces in a pack of cards = 2
∴ P (an ace and black card) = \(\frac{2}{52}\) = \(\frac{1}{26}\)
Ch 15 Maths Class 10 Extra Questions Question 4.
A card is drawn at random from a pack of 52 playing cards. Find the probability that the card drawn is neither an ace nor a king.
Solution:
Let E be the event card drawn is neither an ace nor a king.
Then, the number of outcomes favourable to the event E = 44 (4 kings and 4 aces are not there)
∴ P(E) = \(\frac{44}{52}\) = \(\frac{11}{13}\)
Probability Class 10 Questions Question 5.
A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out (i) an orange flavoured candy? (ii) a lemon flavoured candy?
Solution:
(i) As the bag contains only lemon flavoured candies. So, the event related to the experiment of taking out an orange flavoured candy is an impossible event. So, its probability is 0.
(ii) As the bag contains only lemon flavoured candies. So, the event related to the experiment of taking out lemon flavoured candies is certain event. So, its probability is 1.
Question 6.
12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Solution:
Here, total number of pens = 132 + 12 = 144
∴ Total number of elementary outcomes = 144
Now, favourable number of elementary events = 132
∴ Probability that a pen taken out is good one = \(\frac{132}{144}\) = \(\frac{11}{12}\)
Question 7.
Two players, Sangeeta and Reshma, play a tennis match. It is known that the probability of Sangeeta’s winning the match is 0.62. What is the probability of Reshma’s winning the match?
Solution:
Let S and R denote the events that Sangeeta and Reshma wins the match, respectively.
The probability of Sangeeta’s winning = P(S) = 0.62
As the events R and S are complementary
∴ The probability of Reshma’s winning = P(R) = 1 – P(S)
= 1 – 0.62 = 0.38.
Question 8.
A child has a die whose six faces show the letters as given below:
![]()
The die is thrown once. What is the probability of getting (i) A? (ii) D?
Solution:
The total number of elementary events associated with random experiment of throwing a die is 6.
(i) Let E be the event of getting a letter A.
∴ Favourable number of elementary events = 2
∴ P(E) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
(ii) Let E be the event of getting a letter D.
∴ Favourable number of elementary events = 1
∴ P(E) = \(\frac{1}{6}\)
Question 9.
A card is drawn at random from a pack of 52 playing cards. Find the probability that the card drawn is neither a red card nor a black king.
Solution:
Let E be the event card drawn is neither a red card nor a black king’
The number of outcomes favourable to the event E = 24 (26 red cards and 2 black kings are not there, so 52 – 28 = 24)
∴ P(E) = \(\frac{24}{52}\) = \(\frac{16}{13}\)
Question 10.
Out of 400 bulbs in a box, 15 bulbs are defective. One bulb is taken out at random from the box. Find the probability that the drawn bulb is not defective.
Solution:
Total number of bulbs in the box = 400
Total number of defective bulbs in the box = 15
Total number of non-defective bulbs in the box = 400 – 15 = 385
![]()
Question 11.
Rahim tosses two different coins simultaneously. Find the probability of getting at least one
tail.
Solution:
The sample space is {HH, HT, TH, TT}
Total number of outcomes = 4
Outcomes for getting at least one tail is {HT, TH, TT}
Number of favourable outcomes = 3
![]()
= \(\frac{3}{4}\)
Probability Class 10 Extra Questions Short Answer Type 2
Question 1.
Harpreet tosses two different coins simultaneously (say, one is of 1 and other of 2). What is the probability that she gets at least one head?
Solution:
When two coins are tossed simultaneously, the possible outcomes are (H, H), (H, T), (T, H), (T, T) which are all equally likely. Here (H, H) means head up on the first coin (say on ₹ 1) and head up on the second coin (₹ 2). Similarly (H, T) means head up on the first coin and tail up on the second coin and so on.
The outcomes favourable to the event E, ‘at least one head’ are (H, H), (H, T) and (T, H). So, the number of outcomes favourable to E is 3.
Therefore, P(E) = \(\frac{3}{4}\)
i.e., the probability that Harpreet gets at least one head is \(\frac{3}{4}\).
Question 2.
A game consists of tossing a one-rupee coin 3 times and noting the outcome each time. Ramesh wins the game if all the tosses give the same result (i.e. three heads or three tails) and loses otherwise. Find the probability of Ramesh losing the game.
Solution:
The outcomes associated with this experiment are given by
HHH, HHT, HTH, THH, TTH, THT, HTT, TTT
∴ Total number of possible outcomes = 8
Now, Ramesh will lose the game if he gets
HHT, HTH, THH, TTH, THT, HTT
∴ Favourable number of events = 6
∴ Probability that he lose the game = \(\frac{6}{8}\) = \(\frac{3}{4}\)
Question 3.
Three unbiased coins are tossed together. Find the probability of getting:
(i) all heads.
(ii) exactly two heads.
(iii) exactly one head.
(iv) at least two heads.
(v) at least two tails
Solution:
Elementary events associated to random experiment of tossing three coins are
HHH, HHT, HTH, THH, HTT, THT, TTH, TTT
∴ Total number of elementary events = 8
(i) The event “getting all heads” is said to occur, if the elementary event HHH occurs, i.e., HHH is an outcome.
∴ Favourable number of elementary events = 1
Hence, required probability = \(\frac{1}{8}\)
(ii) The event “getting two heads” will occur, if one of the elementary events HHT, THH, HTH occurs.
∴ Favourable number of elementary events = 3
Hence, required probability = \(\frac{3}{8}\)
(iii) The event of “getting one head”, when three coins are tossed together, occurs if one of the elementary events HTT, THT, TTH, occurs.
Favourable number of elementary events = 3
Hence, required probability = \(\frac{3}{8}\)
(iv) If any of the elementary events HHH, HHT, HTH, and THH is an outcome, then we say that
the event “getting at least two heads” occurs.
∴ Favourable number of elementary events = 4
honom 4 Hence, required probability = \(\frac{4}{8}\) = \(\frac{1}{2}\)
(v) Similar as (iv) P (getting at least two tails) = \(\frac{4}{8}\) = \(\frac{1}{2}\)
Question 4.
A die is thrown once. Find the probability of getting:
(i) a prime number.
(ii) a number lying between 2 and 6.
(iii) an odd number.
Solution:
We have, the total number of possible outcomes associated with the random experiment of throwing a die is 6 (i.e., 1, 2, 3, 4, 5, 6).
(i) Let E denotes the event of getting a prime number.
So, favourable number of outcomes = 3 (i.e., 2, 3, 5)
∴ P(E) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
(ii) Let E be the event of getting a number lying between 2 and 6.
∴ Favourable number of elementary events (outcomes) = 3 (i.e., 3, 4, 5)
∴ P(E) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
(iii) Let E be the event of getting an odd number.
∴ Favourable number of elementary events = 3 (i.e., 1, 3, 5)
∴ P(E) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
Question 5.
Suppose we throw a die once.
(i) What is the probability of getting a number greater than 4?
(ii) What is the probability of getting a number less than or equal to 4?
Solution:
(i) Here, let E be the event getting a number greater than 4′. The number of possible outcomes are six : 1, 2, 3, 4, 5 and 6, and the outcomes favourable to E are 5 and 6. Therefore, the number of outcomes favourable to E is 2. So,
P(E) = P (number greater than 4) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
(ii) Let F be the event ‘getting a number less than or equal to 4’.
Number of possible outcomes = 6
Outcomes favourable to the event F are 1, 2, 3, 4.
So, the number of outcomes favourable to F is 4.
Therefore, P(F) = \(\frac{4}{6}\) = \(\frac{2}{3}\)
Question 6.
One card is drawn from a well-shuffled deck of 52 cards. Calculate the probability that the card will:
(i) be an ace.
(ii) not be an ace.
Solution:
Well-shuffling ensures equally likely outcomes.
(i) There are 4 aces in a deck. Let E be the event ‘the card is an ace’.
The number of outcomes favourable to E = 4.
The number of possible outcomes = 52
Therefore, P(E) = \(\frac{4}{52}\) = \(\frac{1}{3}\).
(ii) Let Ē be the event ‘card drawn is not an ace’.
The number of outcomes favourable to the event Ē = 52 – 4 = 48.
The number of possible outcomes = 52.
Therefore, P(Ē) = \(\frac{48}{52}\) = \(\frac{12}{13}\)
Question 7.
Five cards – the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is (a) an ace? (b) a queen?
Solution:
Here, the total number of possible outcomes = 5.
(i) Since, there is only one queen
∴ Favourable number of elementary events = 1
∴ Probability of getting the card of queen = \(\frac{1}{5}\)
(ii) Now, the total number of possible outcomes = 4.
(a) Since, there is only one ace
∴ Favourable number of elementary events = 1
∴ Probability of getting an ace card = \(\frac{1}{4}\)
(b) Since, there is no queen (as queen is put aside)
∴ Favourable number of elementary events = 0
∴ Probability of getting a queen = \(\frac{0}{4}\)
Question 8.
A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be (i) red ? (ii) white? (iii) not green?
Solution:
Here, total number of marbles = 17
∴ Total number of possible outcomes = 17.
(i) Since, there are 5 red marbles in the box.
∴ Favourable number of elementary events = 5
∴ Probability of getting red marble = \(\frac{5}{17}\)
(ii) Since, there are 8 white marbles in the box.
∴ Favourable number of elementary events = 8
∴ Probability of getting white marble = \(\frac{8}{17}\)
(iii) Since, there are 5 + 8 = 13 marbles which are not green in the box.
∴ Favourable number of elementary events = 13
∴ Probability of not getting a green marble = \(\frac{13}{17}\)
Question 9.
A bag contains 5 black, 7 red and 3 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is:
(i) red.
(ii) black or white.
(iii) not black.
Solution:
Total number of balls = 5 + 7 + 3 = 15
Number of red balls = 7, Number of black or white = 5 + 3 = 8 balls
Number of not black = 7 + 3 = 10 balls
![]()
(1) P (red ball) = \(\frac{7}{15}\)
(ii) P (black or white ball) = \(\frac{8}{15}\)
(iii) P (not black ball) = \(\frac{10}{15}\) = \(\frac{2}{2}\)
Question 10.
A bag contains 5 red, 8 white and 7 black balls. A ball is drawn at random from the bag. Find the probability that the drawn ball is: (i) red or white. (ii) not black. (iii) neither white nor black.
Solution:
Total number of balls = 5 + 8 + 7 = 20
(i) P (red or white) = \(\frac{5+8}{20}\) = \(\frac{13}{20}\)
(ii) P (not black) = 1 – P (black) = 1 – \(\frac{7}{20}\) = \(\frac{13}{20}\)
(iii) P (neither white nor black) = P (Red balls) = \(\frac{5}{20}\) = \(\frac{1}{4}\)
Question 11.
It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
Solution:
Let E be the event of having the same birthday.
Therefore, Ē is the event of not having the same birthday.
i.e., P (Ē) = 0.992 (Given)
Now, we have
P(E) + P(Ē) = 1 ⇒ P(E) = 1 – P(E) = 1 -0.992 = 0.008.
Question 12.
1000 tickets of a lottery were sold and there are 5 prizes on these tickets. If Saket has purchased one lottery ticket, what is the probability of winning a prize ?
Solution:
Out of 1000 lottery tickets, one ticket can be chosen in 1000 ways.
∴ Total number of elementary events = 1000
It is given that there are 5 prizes on these 1000 tickets.
Therefore, number of ways of selecting a prize ticket = 5 .
∴ Favourable number of elementary events
Hence, P (Winning a prize) = \(\frac{5}{1000}\) = \(\frac{1}{200}\)
Question 13.
In a single throw of a pair of different dice, what is the probability of getting (i) a prime number on each dice ? (ii) a total of 9 or 11 ?
Solution:
Total outcomes = 36
(i) Favourable outcomes are (2, 2) (2, 3) (2, 5) (3, 2) (3, 3) (3, 5) (5, 2) (5, 3) (5, 5) i.e., 9 outcomes.
P (a prime number on each die) = \(\frac{9}{36}\) or \(\frac{1}{4}\)
(ii) Favourable outcomes are (3,6) (4, 5) (5, 4) (6, 3) (5, 6) (6, 5) i.e., 6 outcomes
P (a total of 9 or 11) = \(\frac{6}{36}\) or \(\frac{1}{6}\)
Question 14.
Two different dice are thrown together. Find the probability that the numbers obtained
(i) have a sum less than 7
(ii) have a product less than 16
(iii) is a doublet of odd numbers.
Solution:
Total number of outcomes = 36
(i) Favourable outcomes are
(1, 1,) (1, 2) (1, 3) (1, 4) (1,5) (2, 1) (2, 2) (2, 3)
(2, 4) (3, 1) (3, 2) (3, 3) (4, 1) (4, 2) (5, 1) i.e., 15
∴ P (sum less than 7) = \(\frac{15}{36}\) or \(\frac{5}{12}\)
(ii) Favourable outcomes are
(1, 1) (1, 2) (1,3) (1, 4) (1,5) (1,6) (2, 1) (2, 2) (2,3)
(2, 4) (2,5) (2, 6) (3, 1) (3, 2) (3, 3) (3, 4) (3,5) (4, 1)
(4, 2) (4, 3) (5, 1) (5, 2) (5, 3) (6, 1) (6, 2) i.e., 25
∴ P (product less than 16) = \(\frac{25}{36}\)
(iii) Favourable outcomes are
(1, 1) (3, 3) (5, 5) 1.e, 3
∴ (doublet of odd number) = \(\frac{3}{36}\) or \(\frac{1}{12}\)
3 or 1
Probability Class 10 Extra Questions Long Answer Type
Question 1.
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting:
(i) a king of red colour.
(ii) a face card.
(iii) a red face card.
(iv) the jack of hearts.
(v) a spade.
(vi) the queen of diamonds.
Solution:
Here, total number of possible outcomes = 52
(i) As we know that there are two suits of red card, i.e., diamond and heart and each suit contains one king.
∴ Favourable number of outcomes = 2
∴ Probability of getting a king of red colour = \(\frac{2}{52}\) = \(\frac{1}{26}\)
(ii) As we know that kings, queens and jacks are called face cards. Therefore, there are 12 face cards.
∴ Favourable number of elementary events = 12
∴ Probability of getting a face card = \(\frac{12}{52}\) = \(\frac{3}{13}\)
(iii) As we know there are two suits of red cards, i.e., diamond and heart and each suit contains 3 face cards.
∴ Favourable number of elementary events = 2 × 3 = 6
∴ Probability of getting red face card = \(\frac{6}{52}\) = \(\frac{3}{26}\)
(iv) Since, there is only one jack of hearts.
∴ Favourable number of elementary events = 1
∴ Probability of getting the jack of heart = \(\frac{1}{52}\)
(v) Since, there are 13 cards of spade.
∴ Favourable number of elementary events = 13
∴ Probability of getting a spade = \(\frac{13}{52}\) = \(\frac{1}{4}\)
(vi) Since, there is only one queen of diamonds.
∴ Favourable number of outcomes (elementary events) = 1
∴ Probability of getting a queen of diamond = \(\frac{1}{52}\)
Question 2.
One card is drawn from a pack of 52 cards, each of the 52 cards being equally likely to be drawn. Find the probability that the card drawn is:
(i) an ace.
(ii) red.
(iii) either red or king.
(iv) red and a king.
(v) a face card.
(vi) a red face card.
(vii) “2′ of spades.
(viii) ’10’ of a black suit.
Solution:
Out of 52 cards, one card can be drawn in 52 ways.
So, total number of elementary events = 52
(i) There are four ace cards in a pack of 52 cards. So, one ace can be chosen in 4 ways.
∴ Favourable number of elementary events = 4
Hence, required probability = \(\frac{4}{52}\) = \(\frac{1}{13}\)
(ii) There are 26 red cards in a pack of 52 cards. Out of 26 red cards, one card can be chosen in 26 ways.
∴ Favourable number of elementary events = 26
Hence, required probability = \(\frac{26}{52}\) = \(\frac{1}{2}\)
(iii) There are 26 red cards, including two red kings, in a pack of 52 playing cards. Also, there are 4 kings, two red and two black. Therefore, card drawn will be a red card or a king if it is any one of 28 cards (26 red cards and 2 black kings).
∴ Favourable number of elementary events = 28
Hence, required probability = \(\frac{28}{52}\) = \(\frac{7}{13}\)
(iv) A card drawn will be red as well as king, if it is a red king. There are 2 red kings in a pack of 52 playing cards.
∴ Favourable number of elementary events = 2
Hence, required probability = \(\frac{2}{52}\) = \(\frac{1}{26}\)
(v) In a deck of 52 cards: kings, queens, and jacks are called face cards. Thus, there are 12 face cards. So, one face card can be chosen in 12 ways.
Favourable number of elementary events = 12
Hence, required probability = \(\frac{12}{52}\) = \(\frac{3}{13}\)
(vi) There are 6 red face cards 3 each from diamonds and hearts. Out of these 6 red face cards, one card can be chosen in 6 ways.
∴ Favourable number of elementary events = 6
Hence, required probability = \(\frac{6}{52}\) = \(\frac{3}{26}\)
(vii) There is only one ‘2’ of spades.
∴ Favourable number of elementary events = 1 Hence, required probability = 2
(viii) There are two suits of black cards viz. spades and clubs. Each suit contains one card bearing number 10.
∴ Favourable number of elementary events = 2
Hence, required probability = \(\frac{2}{52}\) = \(\frac{1}{26}\)
Question 3.
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2,3,4,5,6,7,8 see Fig, and these are equally likely outcomes. What is the probability that it will point at: (i) 8? (ii) an odd number? (iii) a number greater than 2? (iv) a number less than 9?
Solution:
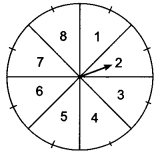
Here, total number of elementary events (possible outcomes) = 8
(i) We have only one ‘P’ on the spining plant.
∴ Favourable number of outcomes = 1
Hence, the probability that arrow points at 8 = \(\frac{1}{26}\).
(ii) We have four odd points (i.e., 1, 3, 5 and 7)
∴ Favourable number of outcomes = 4
∴ Probability that arrow points at an odd number = \(\frac{4}{8}\) = \(\frac{1}{2}\)
(iii) We have 6 numbers greater than 2, i.e., 3, 4, 5, 6, 7 and 8.
Therefore, favourable number of outcomes = 6
∴ Probability that arrow points at a number greater than 2 = \(\frac{6}{8}\) = \(\frac{3}{4}\)
(iv) We have 8 numbers less than 9, i.e, 1, 2, 3, … 8.
∴ Favourable number of outcomes = 8
∴ Probability that arrow points at a number less than 9 = \(\frac{8}{8}\) = 1.
Question 4.
Two dice, one blue and one grey, are thrown at the same time. Write down all the possible outcomes. What is the probability that the sum of the two numbers appearing on the top of the dice is: (i) 8? (ii) 13? (iii) less than or equal to 12?
Solution:
When the blue die shows ‘l’, the grey die could show any one of the numbers 1, 2, 3, 4, 5, 6.
The same is true when the blue die shows ‘2’, ‘3’, ‘4’, ‘5’ or ‘6’. The possible outcomes of the experiment are listed in the table below; the first number in each ordered pair is the number appearing on the blue die and the second number is that on the grey die. So, the number of possible outcomes = 6 × 6 = 36.
(i) The outcomes favourable to the event the sum of the two numbers is 8′ denoted by E, are :
(2, 6), (3, 5), (4, 4), (5, 3), (6, 2) (see figure)
i.e., the number of outcomes favourable to E = 5.
Hence, P(E) = \(\frac{5}{36}\)
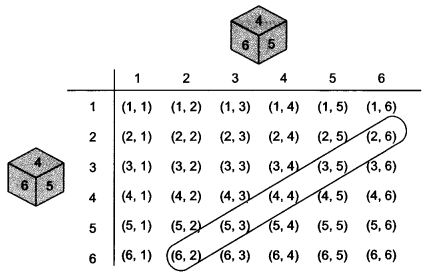
(ii) As you can see from figure, there is no outcome favourable to the event F, ‘the sum of two numbers is 13’.
So, P(F) = \(\frac{0}{36}\) = 0
(iii) As you can see from figure, all the outcomes are favourable to the event G, ‘sum of two numbers ≤ 12.
So, P(G) = \(\frac{36}{36}\) = 1.
Question 5.
A bag contains cards numbered from 1 to 49. A card is drawn from the bag at random, after mixing the cards throughly. Find the probability that the number on the drawn card is:
(i) an odd number.
(ii) a multiple of 5.
(iii) a perfect square.
(iv) an even prime number.
Solution:
Total number of cards = 49
Total number of outcomes = 49
(i) Odd number
Favourable outcomes : 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49
Number of favourable outcomes = 25

Question 6.
All the black face cards are removed from a pack of 52 playing cards. The remaining cards are well shuffled and then a card is drawn at random. Find the probability of getting a:
(i) face card.
(ii) red card.
(iii) black card.
(iv) king.
Solution:
Cards remaining after removing black face cards = red cards + black cards excluding face cards
= 26 + 20 = 46
Total number of possible outcomes = 46
(i) Face Card
Favourable outcomes: 6 red face cards (king, queen and jack of diamond and heart suits)

Question 7.
Cards numbered from 11 to 60 are kept in a box. If a card is drawn at random from the box, find the probability that the number on the drawn card is:
(i) an odd number.
(ii) a perfect square number.
(iii) divisible by 5.
(iv) a prime number less than 20.
Solution:
No. of possible outcomes = 60 – 11 + 1 = 50.
(i) An odd number
Favourable outcomes : 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59
No. of favourable outcomes = 25
Number of favourable outcomes
= \(\frac{25}{50}\) = \(\frac{1}{2}\)
(ii) A perfect square number
Favourable outcomes : 16, 25, 36, 49
No. of favourable outcomes = 04
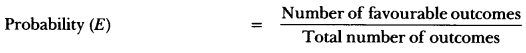
= \(\frac{4}{50}\) = \(\frac{2}{25}\)
(iii) Divisible by 5
Favourable outcomes : 15, 20, 25, 30, 35, 40, 45, 50, 55, 60
No. of favourable outcomes = 10
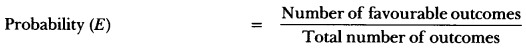
= \(\frac{10}{50}\) = \(\frac{1}{5}\)
(iv) A prime number less than 20
Favourable outcomes : 11, 13, 17, 19
No. of favourable outcomes = 4
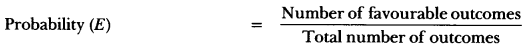
= \(\frac{4}{50}\) = \(\frac{2}{25}\)
Question 8.
A number x is selected at random from the numbers 1, 2, 3 and 4. Another number y is selected at random from the numbers 1, 4, 9 and 16. Find the probability that product of x and y is less than 16.
Solution:
x can be any one of 1, 2, 3 or 4.
y can be any one of 1, 4, 9 or 16
Total number of cases of product of x and y = 16
Product less than 16 = (1 × 1, 1 × 4, 1 × 9, 2 × 1, 2 × 4, 3 × 1, 3 × 4, 4 × 1)
Number of cases, where product is less than 16 = 8
∴ Required probability = \(\frac{8}{16}\) or \(\frac{1}{2}\)
Question 9.
In Fig, shown a disc on which a player spins an arrow twice. The function \(\frac{a}{b}\) is formed, where ‘a’ is the number of sector on which arrow stops on the first spin and ‘b’ is the number of the sector in which the arrow stops on second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the fraction \(\frac{a}{b}\) > 1.
Solution:
For alb > 1, when a = 1, b can not take any value,
a = 2, b can take 1 value,
a = 3, b can take 2 values,
a = 4, b can take 3 values,
a = 5, b can take 4 values,
a = 6, b can take 5 values.
Total possible outcomes = 36
![]()
Question 10.
Two different dice are thrown together. Find the probability that the numbers obtained have
(i) even sum, and (ii) even product.
Solution:
Total number of outcomes = 36[(1, 1), (1, 2) … (6,6)]
Number of outcomes when sum is even = 18 [(1, 1), (1, 3) …(6, 6)]
Number of outcomes when product is even = 27 [(1, 2), (1, 4) … (6,6)]
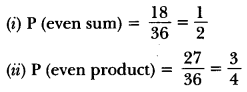
Probability Class 10 Extra Questions HOTS
Question 1.
A die is thrown twice. What is the probability that
(i) 5 will not come up either time?
(ii) 5 will come up at least once?
Solution:
(i) Favourable outcomes are
[(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3,6), (4, 1), (4,2), (4, 3), (4, 4), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 6)]
Total outcomes = 36
∴ Required probability = \(\frac{25}{36}\)
(ii) Probability that 5 will come atleast once = 1 – P (5 will not come up either time)
= 1 – \(\frac{25}{36}\) = \(\frac{11}{36}\)
Question 2.
Find the probability that in a leap year there will be 53 Tuesdays.
Solution:
Leap year = 366 days = (52 × 7 + 2) days = 52 weeks and 2 days.
Thus, a leap year always has 52 Tuesdays. The remaining 2 days can be:
- Sunday and Monday
- Monday and Tuesday
- Tuesday and Wednesday
- Wednesday and Thursday
- Thursday and Friday
- Friday and Saturday
- Saturday and Sunday
Out of these 7 cases, we have Tuesdays in two cases
∴ P(53 Tuesdays) = \(\frac{2}{7}\)
Question 3.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball from the bag is thrice that of a red ball, find the number of blue balls in the bag.
Solution:
Let there be x blue balls in the bag.
∴ Total number of balls in the bag = (5 + x)

Hence, there are 15 blue balls in the bag.
Question 4.
Apoorv throws two dice once and computes the product of the numbers appearing on the dice. Peehu throws one die and squares the number that appears on it. Who has the better chance of getting the number 36? Why?
Solution:
Apoorv throws two dice once.
So, total number of outcomes, n(S) = 36.
Number of outcomes for getting product 36,
n(E2) = 1 [(6 × 6)]
∴ Probability for Apoorv getting the number 36
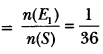
Also, Peehu throw one die.
So, total number of outcomes n(S) = 6
Number of outcomes for getting square of a number as 36.
n(E2) = 1 (∵ 62 = 36)
∴ Probability for Peehu getting the number 36
![]()
Hence, Peehu has better chance of getting the number 36.
