Quadratic Equations Class 10 Extra Questions Maths Chapter 4 with Solutions Answers

Here we are providing Pair of Quadratic Equations Class 10 Extra Questions Maths Chapter 4 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/

Extra Questions for Class 10 Maths Quadratic Equations with Answers Solutions

Extra Questions for Class 10 Maths Chapter 4 Quadratic Equations with Solutions Answers

Quadratic Equations Class 10 Extra Questions Very Short Answer Type

Quadratic Equation Class 10 Extra Questions Question 1.
What will be the nature of roots of quadratic equation 2x² + 4x – n = 0?
Solution:
D = b² – 4ac
⇒ 4² – 4 x 2 (-7)
⇒ 16 + 56 = 72 > 0
Hence, roots of quadratic equation are real and unequal.

Quadratic Equation Extra Questions Question 2.
If \(\frac{1}{2}\) is a root of the equation x² + kx – \(\frac{5}{4}\) = 0, then find the value of k.
Solution:
∴ \(\frac{1}{2}\) is a root of quadratic equation.
∴ It must satisfy the quadratic equation.

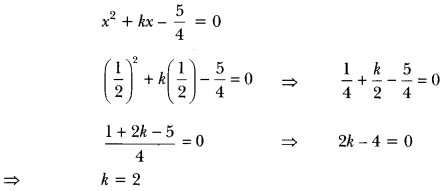
Quadratic Equations Class 10 Extra Questions Question 3.
If ax² + bx + c = 0 has equal roots, find the value of c.
Solution:
For equal roots D = 0
i.e., b² – 4ac = 0
⇒ b² = 4 ac
⇒ c = \(\frac{b^{2}}{4 a}\)

Quadratic Equation Class 10 Questions Question 4.
If a and b are the roots of the equation x² + ax – b = 0, then find a and b.
Solution:
Sum of the roots = a + b = – \(\frac{B}{A}\) = – a
Product of the roots = ab = \(\frac{B}{A}\) = – b
= a + b = – a and ab = -b
⇒ 2a = -b and a = -1
⇒ b = 2 and a = -1

Class 10 Maths Chapter 4 Extra Questions With Solutions Question 5.
Show that x = – 2 is a solution of 3x² + 13x + 14 = 0.
Solution:
Put the value of x in the quadratic equation,
⇒ LHS = 3x² + 13x + 14
⇒ 3(-2)² + 13(-2) + 14
⇒ 12 – 26 + 14 = 0
⇒ RHS Hence, x = -2 is a solution.

Quadratic Equation Class 10 Extra Questions With Answers Question 6.
Find the discriminant of the quadratic equation 4√2x² + 8x + 2√2 = 0).
Solution:
D = 62 – 4ac = (8)² – 4(4√2)(2√2)
⇒ 64 – 64 = 0

Quadratic Equations Class 10 Extra Questions Short Answer Type 1

Class 10 Quadratic Equation Extra Questions Question 1.
State whether the equation (x + 1)(x – 2) + x = 0 has two distinct real roots or not. Justify your answer.
Solution:
(x + 1)(x – 2) + x = 0
⇒ x² – x – 2 + x = 0
⇒ x² – 2 = 0
D = b² – 4ac
⇒ (-4(1)(-2) = 8 > 0
∴ Given equation has two distinct real roots.

Extra Questions Of Quadratic Equations Class 10 Question 2.
Is 0.3 a root of the equation x² – 0.9 = 0? Justify.
Solution:
∵ 0.3 is a root of the equation x² – 0.9 = 0
∴ x² – 0.9 = (0.3)² – 0.9 = 0.09 – 0.9 ≠ 0
Hence, 0.3 is not a root of given equation.

Quadratic Equations Extra Questions Question 3.
For what value of k, is 3 a root of the equation 2x² + x + k = 0?
Solution:
3 is a root of 2x² + x + k = 0, when
⇒ 2(3)² + 3 + k = 0
⇒ 18+ 3 + k = 0
⇒ k = – 21

Quadratic Equation Class 10 Important Questions With Solutions Question 4.
Find the values of k for which the quadratic equation 9x² – 3kx + k = 0 has equal roots.
Solution:
For equal roots:
D = 0
⇒ b² – 4ac = 0
⇒ (- 3k)² – 4 × 9 × k = 0
⇒ 9k² = 36k
⇒ k = 4

Class 10 Quadratic Equations Extra Questions Question 5.
Find the value of k for which the equation x² + k(2x + k – 1)+ 2 = 0 has real and equal roots.
Solution:
Given quadratic equation: x² + k(2x + k-1) + 2 = 0)
= x² + 2kx + (k² – k + 2) = 0
For equal roots, b² – 4ac = 0
⇒ 4k² – 4k² + 4k – 8 = 0
⇒ 4k = 8
⇒ k = 2

Quadratic Equation Questions For Class 10 Question 6.
If -5 is a root of the quadratic equation 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, then find the value of k.
Solution:
Since – 5 is a root of the equation 2x² + px – 15 = 0
∴ 2(-5)² + p(-5) – 15 = 0
⇒ 50 – 5p – 15 = 0 or 5p = 35 or p = 7
Again p(x² + x) + k = 0 or 7x² + 7x + k = 0 has equal roots
∴ D = 0
i.e., b² – 4ac = 0 or 49- 4 × 7k = 0
⇒ k = \(\frac{49}{28}\) = \(\frac{7}{4}\)

Extra Questions On Quadratic Equations Class 10 Question 7.
Does there exist a quadratic equation whose coefficients are rational but both of its roots are irrational? Justify your answer.
Solution:
Yes, x² – 4x + 1 = 0 is a quadratic equation with rational co-efficients.

Questions On Quadratic Equations Class 10 Question 8.
Write the set of values of k for which the quadratic equation 2x² + kx + 8 = 0 has real roots.
Solution:
For real roots, D ≥ 0
⇒ b² – 4ac ≥ 0
⇒ k² – 4(2)(8) ≥ 0
⇒ k² – 64 ≥ 0
⇒ k² ≥ 64
⇒ k ≤ -8 and k ≥ 8

Class 10 Maths Quadratic Equations Extra Questions Question 9.
Solve the quadratic equation 2x² + ax – a² = 0 for x.
Solution:
2x² + ax – a² = 0
Here, a = 2, b = a and c = -a².
Using the formula,

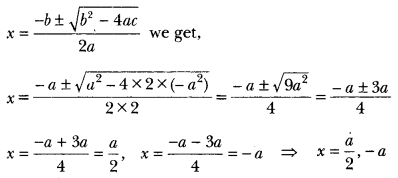
Class 10 Quadratic Equations Important Questions Question 10.
Find the roots of the quadratic equation
Solution:
The given quadratic equation is
√2x² + 7x + 5√2 = 0
By applying mid term splitting, we get
√2x² + 2x + 5x + 5√2 = 0
⇒ √2x(x + √2) + 5(x + √2)
⇒ (√2x + 5) + 5(x + √2) = 0
⇒ x = \(\frac{-5}{\sqrt{2}}/latex], -√2 or [latex]\frac{-5 \sqrt{2}}{2}\), -√2

Quadratic Equation Class 10 Extra Questions Pdf Question 11.
Find the values of p for which the quadratic equation 4x² + px + 3 = 0 has equal roots.
Solution:
For equal roots;
D = 0
⇒ b² – 4ac = 0
⇒ p² – 4 × 4 × 3 = 0
⇒ p² – 48 = 0
⇒ p² = 48
⇒ p = ± √48
⇒ p = 4√3 or -4√3

Ch 4 Maths Class 10 Extra Questions Question 12.
Solve for x: √13x? – 2√3x – 2√3 = 0
Solution:
√3x² – 2√3x – 2√3 = 0
⇒ √3x² – 3√2x + √2x – 2√3 = 0
⇒ √3x(x – √6) + √2(x – √6) = 0
⇒ (√3x + 2)(x – √6) = 0
⇒ √3x + √2 = 0 or x – √6 = 0
⇒ x = \(\frac{-√2}{√3}\) or x = √6

Chapter 4 Maths Class 10 Extra Questions Question 13.
If x = \(\frac{2}{3}\) and x = -3 are roots of the quadratic equation ax² + 7x + b = 0, find the values of a and b.
Solution:
Let us assume the quadratic equation be Ax² + Bx + C = 0.
Sum of the roots = –\(\frac{B}{A}\)

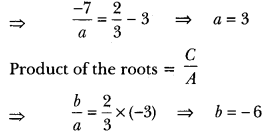
Class 10 Maths Ch 4 Extra Questions Question 14.
A two-digit number is four times the sum of the digits. It is also equal to 3 times the product of digits. Find the number.
Solution:
Let the ten’s digit be x and unit’s digit = y
Number 10x + y

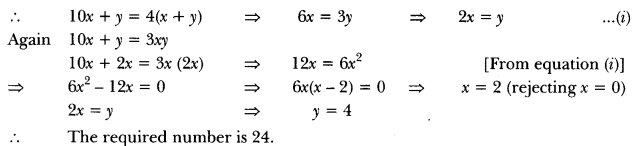
Extra Questions For Quadratic Equation Class 10 Question 15.
Find the value of p, for which one root of the quadratic equation px² – 14x + 8 = 0 is 6 times the other.
Solution:
Let the roots of the given equation be a and 6α.
Thus the quadratic equation is (x – a) (x – 6α) = 0
⇒ x² – 7αx + 6α² = 0 …(i)
Given equation can be written as

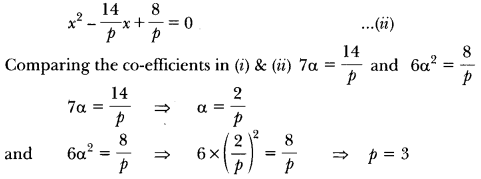
Question 16.
If ad ≠ bc, then prove that the equation
(a² + b²) x² + 2(ac + bd)x + (c²+ d²) = 0 has no real roots.
Solution:
The given quadratic equation is (a² + b²⁾x² + 2(ac + bd)x +(c²+ d²) = 0
D = b² – 4ac
= 4(ac + bd)² – 4(a² + b²) (c²+ d²)
= -4(a²d² + b²c²– 2abcd) = – 4(ad – bc)²
Since ad ≠ bc
Therefore D < 0
Hence, the equation has no real roots.

Question 17.
Solve for x: √13x² – 2x – 8√3 = 0
Solution:
√3x² – 2x – 8√3 = 0
By mid term splitting
⇒ √3x² – 6x + 4x – 8√3 = 0
⇒ √3x(x – 2/3) + 4 (x – 2/3) = 0
⇒ (x – 2√3)(√3x + 4) = 0
⇒ Either (x – 2√3) = 0 or (√3x + 4) = 0
⇒ x = \(\frac{-4}{\sqrt{3}}\), 2√3

Quadratic Equations Class 10 Extra Questions Short Answer Type 2

Question 1.
Find the roots of the following quadratic equations by factorisation:
(i) √2x² + 7x + 5√2 = 0 (ii) 2x² – x + \(\frac{1}{8}\) = 0
Solution:
(i) We have, √2x² + 7x + 5√2 = 0
= √2x² + 5x + 2x + 5√2 = 0
x(√2x + 5) + √2 (√2x + 5) = 0
= (√2x + 5)(x + √2) = 0
∴ Either √2x + 5 = 0 or x + √2 = 0
∴ x = – \(\frac{5}{\sqrt{2}}\) or x = -√2
Hence, the roots are – \(\frac{5}{\sqrt{2}}\) and -√2.
(ii) We have, 2x² – x + \(\frac{1}{8}\) = 0

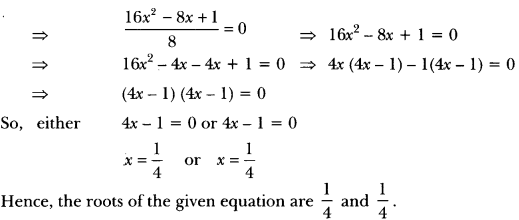
Question 2.
Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) 2x² + x – 4 = 0
(ii) 4x² + 4√3x + 3 = 0
Solution:
(i) We have, 2x² + x – 4 = 0
On dividing both sides by 2, we have

(ii) We have, 4x² + 4√3x + 3 = 0

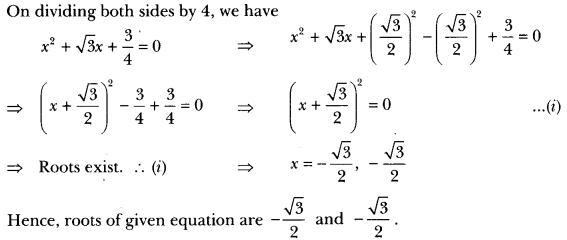
Question 3.
Find the roots of the following quadratic equations by applying the quadratic formula.
(i) 2x² – 7x + 3 = 0
(ii) 4x² + 4√3x + 3 = 0
Solution:
(i) We have, 2x² – 7x + 3 = 0
Here, a = 2, b = -7 and c = 3
Therefore, D = b² – 4ac
⇒ D = (-7)² – 4 × 2 × 3 = 49 – 24 = 25
∵ D > 0, ∴ roots exist.

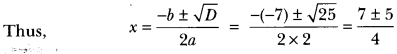
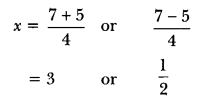
So, the roots of given equation are 3 and \(\frac{1}{2}\)

(ii) We have, 4x² + 4√3x + 3 = 0
Here, a = 4, b = 4√3 and c = 3
Therefore, D = b² – 4ac = (4√3)² – 4 × 4 × 3 = 48 – 48 = 0
∴ D = 0, roots exist and are equal.

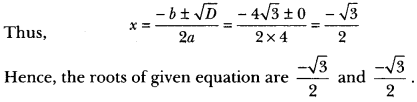
Question 4.
Using quadratic formula solve the following quadratic equation:
p²x² + (p² – q²) x – q² = 0
Solution:
We have, p²x² + (p² – q²) x – q² = 0
Comparing this equation with ax² + bx + c = 0, we have
a = p², b = p² – q² and c = – q²
∴ D = b² – 4ac
⇒ (p² – q)² – 4 × p² × (-q²)
⇒ (p² – q²)² + 4p²q²
⇒ (p² + q³)² > 0
So, the given equation has real roots given by

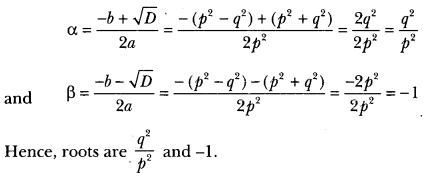
Question 5.
Find the roots of the following equation:

Solution:

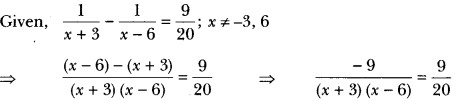
⇒ (x + 3) (x – 6)
⇒ -20 or x² – 3x + 2 = 0
⇒ x² – 2x -x + 2 = 0
⇒ x(x – 2) -1(x – 2) = 0)
⇒ (x – 1) (x – 2) = 0
⇒ x = 1 or x = 2
Both x = 1 and x = 2 are satisfying the given equation. Hence, x = 1, 2 are the solutions of the equation.

Question 6.
Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
(i) 3x² – 4√3x + 4 = 0) (ii) 2x² – 6x + 3 = 0
Solution:
(i) We have, 3x² – 4√3x + 4 = 1
Here, a = 3, b = – 4√3 and c = 4
Therefore,
D = b² – 4ac
⇒ (- 4√3)² – 4 × 3 × 4
⇒ 48 – 48 = 0
Hence, the given quadratic equation has real and equal roots.

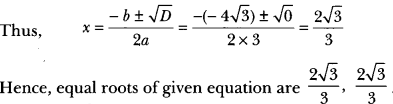
(ii) Wehave, 2x² – 6x + 3 = 0
Here, a = 2, b = -6, c = 3
Therefore, D = b² – 4ac
= (-6)² 4 × 2 × 3 = 36 – 24 = 12 > 0
Hence, given quadratic equation has real and distinct roots.

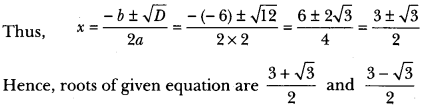
Question 7.
Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(i) 2x² + kx + 3 = 0
(ii) kx (x – 2) + 6 = 0
Solution:
(i) We have, 2x² + kx + 3 = 0
Here, a = 2, b = k, c = 3
D = b² – 4ac = k² – 4 × 2 × 3 = k² – 24 For equal roots
D = 0
i.e., k² – 24 = 0
⇒ ķ² = 24
⇒ k = ± √24
⇒ k = + 2√6

(ii) We have, kx(x – 2) + 6 = 0
⇒ kx² – 2kx + 6 = 0
Here, a = k, b = – 2k, c = 6
For equal roots, we have
D = 0
i.e., b² – 4ac = 0
⇒ (-2k)² – 4 × k × 6 = 0
⇒ 4k² – 24k = 0
⇒ 4k (k – 6) = 0
Either 4k = 0 or k – 6 = 0
⇒ k = 0 or k = 6
But k = 0 6)ecause if k = 0 then given equation will not be a quadratic equation).
So, k = 6.

Question 8.
If the roots of the quadratic equation (a – b) x² + (b – c) x + (c – a) = 0 are equal, prove that 2a = b + c.
Solution:
Since the equation (a – b)x² + (b – c) x + (c – a) = 0 has equal roots, therefore discriminant
D = (b – c)² – 4(a – b) (c – a) = 0
⇒ b² + c²– 2bc – 4(ac – a² – bc + ab)
⇒ b² + c²– 2bc – 4ac + 4a² + 4bc – 4ab = 0
⇒ 4a² + b² + c²– 4ab + 2bc – 4ac = 0
⇒ (2a)² + (- b)² + (-c)² + 2(2a) (-b) + 2(-b) (-c) + 2(-c) 2a = 0
⇒ (2a – b – c)² = 0
⇒ 2a – b – c = 0
⇒ 2a = b + c. Hence Proved

Question 9.
If the equation (1 + m²)x² + 2mcx + c²– a² = 0 has equal roots, show that c²= a² (1 + m²).
Solution:
The given equation is (1 + m²) x² + (2mc) x + (c²– a²) = 0
Here, A = 1 + m², B = 2mc and C = c²– a²
Since the given equation has equal roots, therefore D = 0 = B² – 4AC = 0.
⇒ (2mc)² – 4(1 + m²) (c²– a²) = 0
⇒ 4m²c²– 4(c²– a² + m²c²– m²a²) = 0
⇒ m²c²– c²+ a² – m²c²+ m²a² = 0. [Dividing throughout by 4]
⇒ – c²+ a² (1 + m²) = 0
⇒ c²= a(1 + m²) Hence Proved

Question 10.
If sin θ and cos θ are roots of the equation ax² + bx + c = 0, prove that a² – b² + 2ac = 0.
Solution:

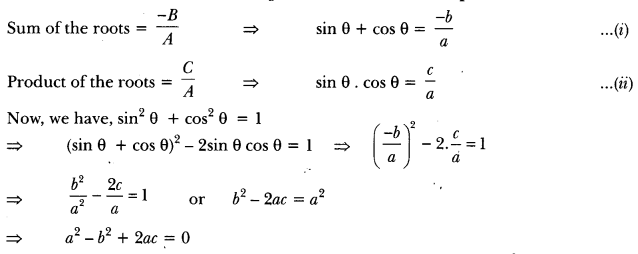
Question 11.
Determine the condition for one root of the quadratic equation ax² + bx + c = 0 to be thrice the other.
Solution:
Let the roots of the given equation be a and 3α.

Question 12.
Salve for

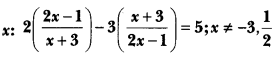
Solution:

⇒ (4x – 2)(2x – 1) – (3x + 9)(x + 3) = 5(x + 3)(2x – 1)
⇒ (8x² – 4x – 4x + 2) – (3x² + 9x + 9x + 27) = 5(2x² – x + 6x – 3)
⇒ 8x² – 8x + 2 – 3x² – 18x – 27 = 10x² + 25x – 15
⇒ 5x² – 26x – 25 = 10x² + 25x – 15
⇒ 5x² + 51x + 10 = 0
⇒ 5x² + 50x + x + 10 = 0
⇒ 5x (x + 10) + 1 (x + 10) = 0
⇒ (5x + 1) (x + 10) = 0
⇒ 5x + 1 = 0 or x + 10 = 0
⇒ x = \(\frac{-1}{5}\) or x = -10

Question 13.
Solve the equation

Solution:

⇒ (4 – 3x) (2x + 3) = 5x ⇒ 8x – 6x² + 12 – 9x = 5x
⇒ 6x² + 6x – 12 = 0
⇒ x² + x – 2 = 0
⇒ x² + 2x + x – 2 = 0
⇒ x(x + 2)-1(x + 2) = 0
⇒ (x – 1)(x + 2) = 0
⇒ x – 1 = 0 or x + 2 = 0
⇒ x = 1 or x = -2

Question 14.
Solve for

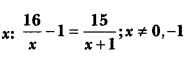
Solution:

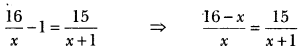
⇒ (16 – x) (x + 1) = 15x
⇒ 16x – x² + 16 – x = 15x
⇒ x² + 15x – 15x – 16 = 0
⇒ x² = 16
⇒ x = ± 4

Question 15.
Solve for x: + 5x – (a² + a – 6) = 0
Solution:
⇒ x² + 5x – (a² + a – 6) = 0
⇒ x² + 5x – (a? + 3a – 2a – 6) = 0
⇒ x² + 5x – [a(a + 3) -2 (a + 3)] = 0
⇒ x² + 5x – (a – 2) (a + 3) = 0
∴ x² + (a + 3)x – (a – 2) x – (a – 2) (a + 3) = 0
⇒ x[x + (a + 3)]-(a – 2) [X + (a + 3)] = 0
⇒ [{x + (a + 3)} {x – (a – 2)}] = 0
∴ x = -(a + 3) or x = (a -2)
⇒ -(a + 3), (a – 2)
Alternative method
x² + 5x -(a² + a – 6) = 0

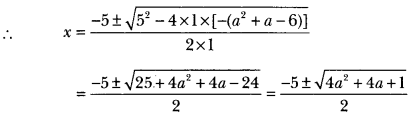
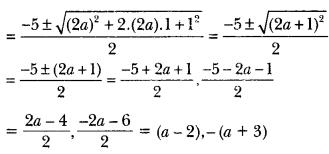
Question 16.
Solve for

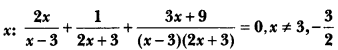
Solution:

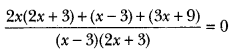
⇒ 2x(2x + 3) + (x – 3) + (3x + 9) = 0
⇒ 4x² + 10x + 6 = 0
⇒ 2x² + 5x + 3 = 0
⇒ (x + 1) (2x + 3) = 0
⇒ x = -1, x = – \(\frac{3}{2}\)
But x ≠ – \(\frac{3}{2}\)
∴ x = -1

Question 17.
Solve for

Solution:

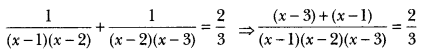
⇒ 3(x – 3 + x – 1) = 2(x – 1)(x – 2)(x – 3)
⇒ 3(2x – 4) = 2(x – 1)(x – 2)(x – 3)
⇒ 3 × 2(x – 2) = 2(x – 1)(x − 2)(x – 3)
⇒ 3 = (x – 1)(x – 3) i.e., x² – 4x = 0
⇒ x(x – 4) = 0 ∴ x = 0, x = 4

Question 18.
If the roots of the equation (c- ab)x² – 2(a²– bc)x + b² – ac = 0 in x are equal, then show that either a = 0 or a³ + b³+ c³ = 3abc.
Solution:
For equal roots D = 0
Therefore 4(a² – bc)² – 4(c² – ab) (b² – ac) = 0
⇒ 4[a⁴ + b²c² – 2a²bc – b²c² + ac³ + ab³ – a²bc] = 0.
⇒ a(a³ + b³ + c³ – 3abc) = 0
Either a = 0 or a³ + b³ + c³ = 3abc

Question 19.
If the roots of the quadratic equation
(x – a) (x – b) + (x – b) (x – c) + (x – c) (x – a) = 0
are equal, then show that a = b = c.
Solution:
Given (x – a) (x – b) + (x – b) (x – c) + (x – 6) (x – a) = 0
⇒ x² – ax – bx + ab + x² – bx – cx + bc + x² – cx – ax + ac = 0
⇒ 3x² – 2(a + b + c)x + ab + bc + ca = 0
Now, for equal roots D = 0
⇒ B² – 4AC = 0
⇒ 4(a + b + c)² – 12(ab + bc + ca) = 0
4a² + 4b² + 4c² + 8ab + 8bc + 8ca – 12ab – 12bc – 12ca = 0
⇒ 2[2a² + 2b² + 2co – 2ab – 2bc – 2ca] = 0
⇒ 2[(a² + b²– 2ab) + (b²+ c² – 2bc) + (c² + a² – 2ca)] = 0
⇒ [(a – b)² + (b – c)² + (c – a)²] = 0
⇒ a – b = 0, b – c = 0, c – a = 0
⇒ a = b, b = c, c = a
⇒ a = b = c

Quadratic Equations Class 10 Extra Questions Long Answers

Question 1.
Using quadratic formula, solve the following equation for x:
abx² + (b² – ac) x – bc = 0
Solution:
We have, abx² + (b² – ac) x – bc = 0
Here, A = ab, B = b² – ac, C = – bc

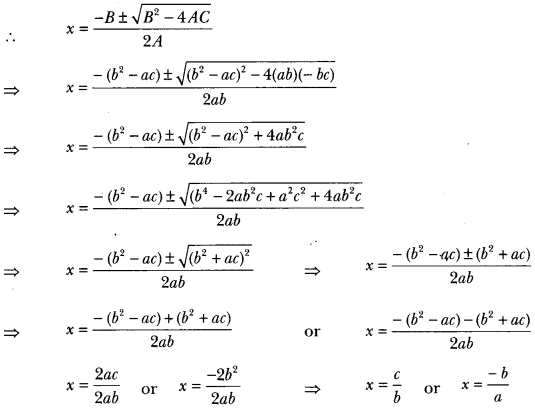
Question 2.
Find the value of p for which the quadratic equation
(2p + 1)x² – (7p + 2)x + (7p – 3) = 0 has equal roots. Also find these roots.
Solution:
Since the quadratic equation has equal roots, D = 0
i.e., b² – 4ac = 0
In (2p + 1 )x² – (7p + 2)x + (7p – 3) = 0
Here, a = (2p + 1), b = -(7p + 2), c = (7p – 3)

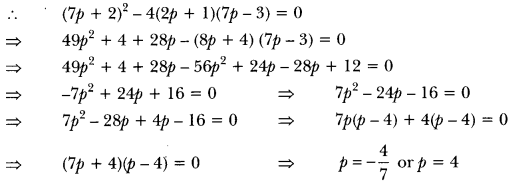
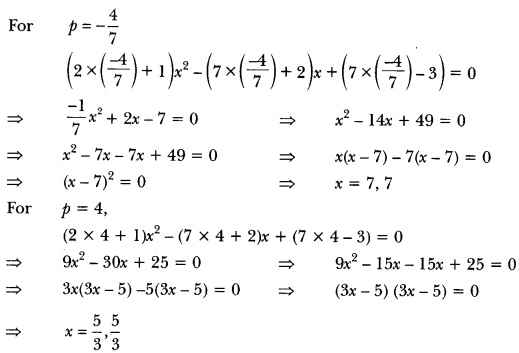
Question 3.
Solve for

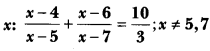
Solution:

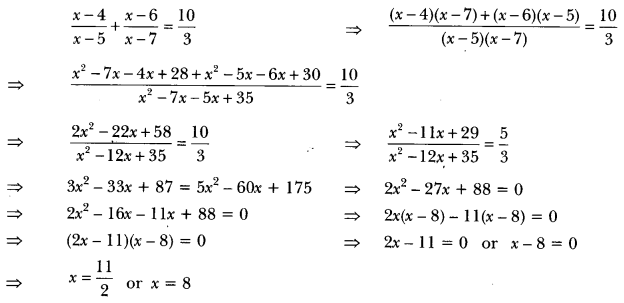
Question 4.
The sum of the reciprocals of Rehman’s age (in years) 3 years ago and 5 years from now is Find his present age.
Solution:
Let the present age of Rehman be x years.
So, 3 years ago, Rehman’s age = (x – 3) years
And 5 years from now, Rehman’s age = (x + 5) years
Now, according to question, we have

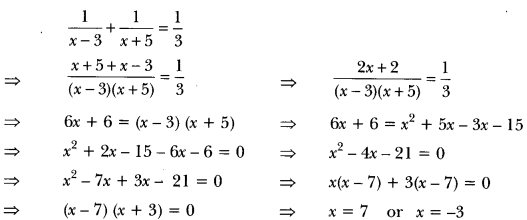
But x ≠ -3 (age cannot be negative)
Therefore, present age of Rehman = 7 years.

Question 5.
The difference of two natural numbers is 5 and the difference of their reciprocals is \(\frac{1}{10}\). Find the numbers.
Solution:
Let the two natural numbers be x and y such that x > y.
According to the question,
Difference of numbers, x – y = 5 ⇒ x = 5 + y …..(i)
Difference of the reciprocals,

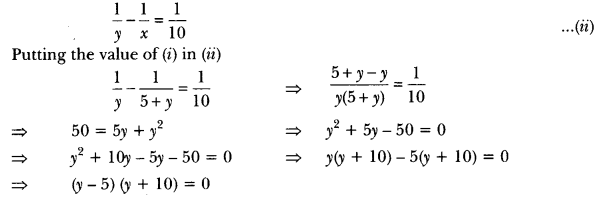
∴ y is a natural number.
∵ y = 5
Putting the value of y in (i), we have
⇒ x = 5 + 5
⇒ x = 10
The required numbers are 10 and 5.

Question 6.
The sum of the squares of two consecutive odd numbers is 394. Find the numbers.
Solution:
Let the two consecutive odd numbers be x and x + 2.

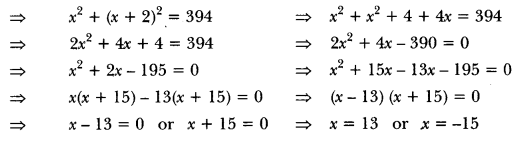
Hence, the numbers are 13 and 15 or -15 and -13.

Question 7.
The sum of two numbers is 15 and the sum of their reciprocals is 3. Find the numbers.
Solution:
Let the numbers be x and 15 – x.
According to given condition,

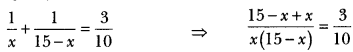
⇒ 150 = 3x(15 – x)
⇒ 50 = 15x – x²
⇒ x² – 15x + 50 = 0
⇒ x² – 5x – 10x + 50 = 0
⇒ x(x – 5) -10(x – 5) = 0
⇒ (x – 5)(x – 10) = 0
⇒ x = 5 or 10.
When x = 5, then 15 – x = 15 – 5 = 10
When x = 10, then 15 – x = 15 – 10 = 5
Hence, the two numbers are 5 and 10.

Question 8.
In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of her marks would have been 210. Find her marks in the two subjects.
Solution:
Let Shefali’s marks in Mathematics be x.
Therefore, Shefali’s marks in English is (30 – x).
Now, according to question,
⇒ (x + 2) (30 – x – 3) = 210
⇒ (x + 2) (27 – x) = 210
⇒ 27x – x² + 54 – 2x = 210
⇒ 25x – x² + 54 – 210 = 0
⇒ 25x – x² – 156 = 0
⇒ -(x² – 25x + 156) = 0
⇒ x² – 25x + 156 = 0
= x² – 13x – 12x + 156 = 0
⇒ x(x – 13) – 12(x – 13) = 0
⇒ (x – 13) (x – 12) = 0
Either x – 13 or x – 12 = 0
∴ x = 13 or x = 12
Therefore, Shefali’s marks in Mathematics = 13
Marks in English = 30 – 13 = 17
or Shefali’s marks in Mathematics = 12
marks in English = 30 – 12 = 18.

Question 9.
A train travels 360 km at a uniform speed. If the speed has been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
Let the uniform speed of the train be x km/h.

But x cannot be negative, so x ≠ – 45
therefore, x = 40
Hence, the uniform speed of train is 40 km/h.

Question 10.
The sum of the areas of two squares is 468 m². If the difference of their perimeters is 24 m, find the sides of the two squares.
Solution:
Let x be the length of the side of first square and y be the length of side of the second square.
Then, x² + y² = 468 …(i)
Let x be the length of the side of the bigger square.
4x – 4y = 24
⇒ x – y = 6 or x = y + 6 …(ii)
Putting the value of x in terms of y from equation (ii), in equation (i), we get
(y + 6)² + y² = 468
⇒ y² + 12y + 36 + y² = 468 or 232 + 12y – 432 = 0
⇒ y² + 6y – 216 = 0
⇒ y² + 18y – 12y – 216 = 0
⇒ y(y + 18) – 12(y + 18) = 0
⇒ (y + 18)(y – 12) = 0
Either y + 18 = 0 or y – 12 = 0
⇒ y = -18 or y = 12
But, sides cannot be negative, so y = 12
Therefore, x = 12 + 6 = 18
Hence, sides of two squares are 18 m and 12 m.

Question 11.
Seven years ago Varun’s age was five times the square of Swati’s age. Three years hence, Swati’s age will be two-fifth of Varun’s age. Find their present ages.
Solution:
Seven years ago, let Swati’s age be x years. Then, seven years ago Varun’s age was 5x² years.
∴ Swati’s present age = (x + 7) years
Varun’s present age = (5x² + 7) years
Three years hence,
Swati’s age = (x + 7 + 3) years = (x + 10) years
Varun’s age (5x² + 7 + 3) years = (5x² + 10) years
According to the question,

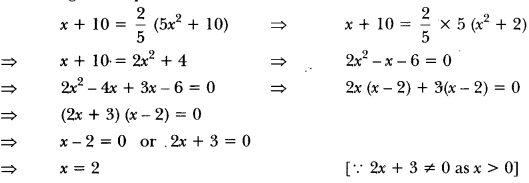
Hence, Swati’s present age = (2 + 7) years = 9 years
and Varun’s present age = (5 × 2² + 7) years = 27 years

Question 12.
A train covers a distance of 300 km at a uniform speed. If the speed of the train is increased by 5 km/hour, it takes 2 hours less in the journey. Find the original speed of the train.
Solution:
Let the original speed of the train = x km/h.

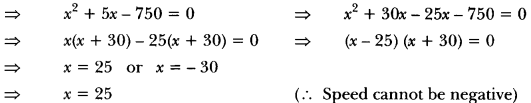
Therefore, the usual speed of the train = 25 km/h.

Question 13.
A two digit number is such that the product of its digits is 18. When 63 is subtracted from the number, the digits interchange their places. Find the number.
Solution:
Let the digit at tens place be x.

Question 14.
If twice the area of a smaller square is subtracted from the area of a larger square; the result is 14 cm². However, if twice the area of the larger square is added to three times the area of the smaller square, the result is 203 cm². Determine the sides of the two squares.
Solution:
Let the sides of the larger and smaller squares be x and y respectively. Then
x² – 2y² = 14 …..(i)
and 2x² + 3y² = 203 ……(ii)
Operating (ii) -2 × (i), we get
⇒ 2x² + 3y² – (2x² – 4y²) = 203 – 2 × 14
⇒ 2x² + 3y² – 2x² + 4y² = 203 – 28
⇒ 7y² = 175
⇒ y² = 25
⇒ y ± 15
⇒ y = 5 [∵ Side cannot be negative]
By putting the value of y in equation (i), we get
x² – 2 × 5 = 14
⇒ x² – 50 = 14 or x² = 64
∴ x = 8 or x = 8
∴ Sides of the two squares are 8 cm and 5 cm.

Question 15.
If Zeba was younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than five times her actual age. What is her age now?
Solution:
Let the present age of Zeba be x years
Age before 5 years = (x – 5) years According to given condition,
⇒ (x – 5)² = 5x + 11
⇒ x² + 25 – 10x = 5x + 11
⇒ x² – 10x – 5x + 25 – 11 = 0
⇒ x² – 15x + 14 = 0
⇒ x² – 14x – x + 14 = 0
⇒ x(x – 14) -1(x – 14) = 0
⇒ (x – 1)(x – 14) = 0
⇒ x – 1 = 0 or x – 14 = 0
x = 1 or x = 14
But present age cannot be 1 year.
∴ Present age of Zeba is 14 years.

Question 16.
A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Solution:
Let the speed of the stream be x km/h.
Speed of motorboat in still water = 18 km/h
Speed of motorboat in upstream = (18 – x) km/h
Speed of motorboat in downstream = (18 + x) km/h
Distance travelled = 24 km.

Speed of motorboat = 6 km/h. (∵Speed cannot be negative)

Question 17.
A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.
Solution:
Let the natural number be x
According to the question,
⇒ x + 12 = \(\frac{60}{x}\)
= x² + 12x – 160 = 0
= x² + 20x – 8x – 160 = 0
= x(x + 20) -8(x + 20) = 0
= (x + 20) (x – 8) = 0
x = -20 (Not possible) or x = 8
Hence, the required natural number is 8.

Question 18.
The sum of the squares of two consecutive multiples of 7 is 637. Find the multiples.
Solution:
Let the two consecutive multiples of 7 be x and x +7.
x² + (x + 7)² = 637
= x² + x² + 49 + 14x = 637
= 2x² + 14x – 588 = 0
= x² + 7x – 294 = 0
= x² + 21x – 14x – 294 = 0
= x(x + 21) – 14(x + 21) = 0
= x(x + 14) (x + 21) = 0
= x = 14 or x = -21
The multiples are 14 and 21.

Question 19.
Solve for

Solution:

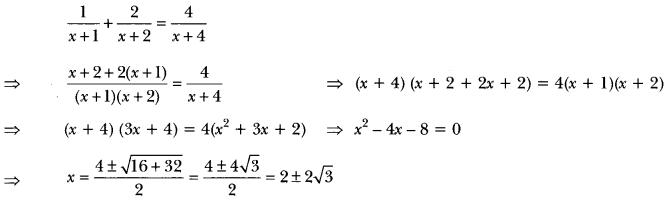
Question 20.
Find the positive value(s) of k for which both quadratic equations x² + kx + 64 = 0 and x² – 8x + k = 0 will have real roots.
Solution:
(i) For x² + kx + 64 = 0 to have real roots
⇒ k² – 4(1)(64) ≥ 0 i.e., k² – 256 ≥ 0
⇒ k ≥ ± 16

(ii) For x² – 8x + k = 0 to have real roots
⇒ (-8)² – 4(k) ≥ 0 i.e., 64 – 4k ≥ 0
⇒ k ≤ ± 16
For (i) and (ii) to hold simultaneously k = 16

Question 21.
Speed of a boat in still water is 15 km/h. It goes 30 km upstream and returns back at the same point in 4 hours 30 minutes. Find the speed of the stream.
Solution:
Let the speed of stream be x km/h.
∴ Speed of boat upstream = (15 – x) km/h.
Speed of boat downstream = (15 + x) km/h.
According to question,

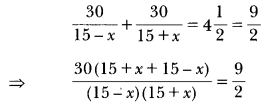
⇒ 30 × 2 × 30 = 9(225 – x²)
⇒ 100 × 2 = 225 – x²
⇒ 200 = 225 – x²
⇒ x² = 25
⇒ x = ±5
⇒ x = 5 (Rejecting – 5)
∴ Speed of stream = 5 km/h

Question 22.
Ram takes 6 days less than Bhagat to finish a piece of work. If both of them together can finish the work in 4 days, in how many days Bhagat alone can finish the work.
Solution:
Let Bhagat alone can do the work in x number of days
∴ Ram takes (x – 6) number of days
Work done by Bhagat in 1 day = \(\frac{1}{x}\)
Work done by Ram in 1 day = \(\frac{1}{x-6}\)
According to the question,

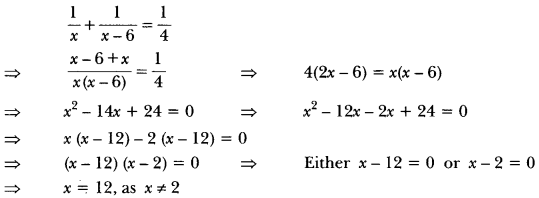
Quadratic Equations Class 10 Extra Questions HOTS

Question 1.
One-fourth of a herd of camels was seen in the forest. Twice the square root of the herd had gone to mountains and the remaining 15 camels were seen on the bank of a river. Find the total number of camels.
Solution:
Let x be the total number of camels.
Then, number of camels in the forest = \(\frac{x}{4}\)
Number of camels on mountains = 2√x
and number of camels on the bank of river = 15

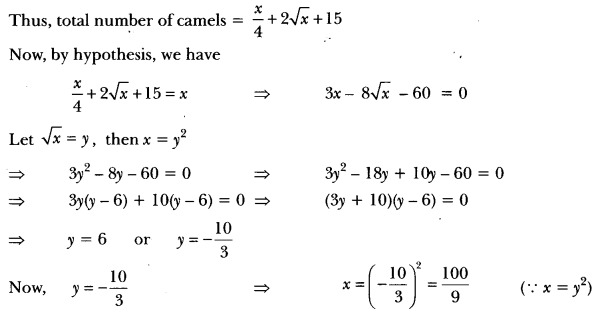
But, the number of camels cannot be a fraction.
∴ y = 6
⇒ x = x² = 36
Hence, the number of camels = 36

Question 2.
Solve the following quadratic equation:
9x² – 9 (a + b) x + [2a² + 5ab + 2b²] = 0.
Solution:
Consider the equation 9x² – 9 (a + b) x + [2a² + 5ab + 2b²] = 0)
Now comparing with Ax² + Bx + C = 0, we get
A = 9, B = -9 (a + b) and C = [2a² + 5ab + 2b²]
Now discriminant, .
D = B² – 4AC

Question 3.
Two taps running together can fill a tank in 3 hours. If one tap takes 3 hours more than the other to fill the tank, then how much time will each tap take to fill the tank?
Solution:
Let, time taken by faster tap to fill the tank be x hours
Therefore, time taken by slower tap to fill the tank = (x + 3) hours
Since the faster tap takes x hours to fill the tank.

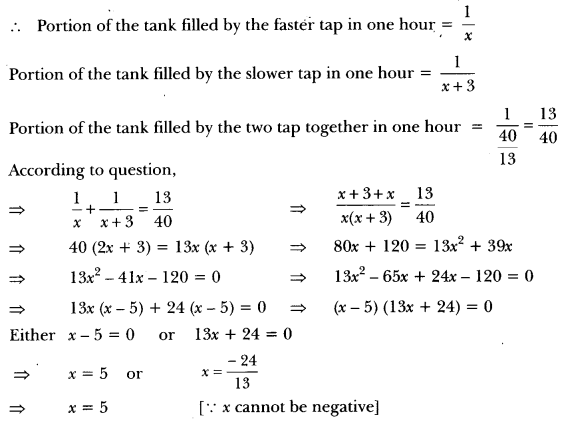
Hence, time taken by faster tap to fill the tank = x = 5 hours
and time taken by slower tap = x + 3 = 5 + 3 = 8 hours.

Question 4.
In a rectangular park of dimensions 50 m × 40 m, a rectangular pond is constructed so that the area of grass strip of uniform width surrounding the pond would be 1184 m². Find the length and breadth of the pond.
Solution:

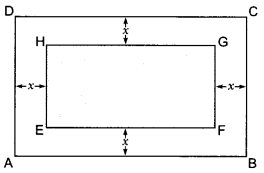
Let ABCD be rectangular lawn and EFGH be rectangular pond. Let x m be the width of grass area, which is same around the pond.
Given, Length of lawn = 50 m
Width of lawn = 40 m
Length of pond = (50 – 2x)m
Breadth of pond = (40 – 2x)m
Also given,
Area of grass surrounding the pond = 1184 m²
⇒ Area of rectangular lawn – Area of pond = 1184 m²
⇒ 50 × 40 – {(50 – 2x) × (40 – 2x)} = 1184
⇒ 2000 – (2000 – 80x – 100x + 4x²) = 1184
⇒ 2000 – 2000 + 180x – 4x² = 1184
⇒ 4x² – 180x + 1184 = 0
⇒ x² – 45x + 296 = 0
⇒ x² – 37x – 8x + 296 = 0
⇒ x(x – 37) – 8(x – 37) = 0
⇒ (x – 37) (x – 8) = 0
⇒ x- 37 = 0 or x – 8 = 0)
⇒ x = 37 or x = 8
x = 37 is not possible as in this case length of pond becomes 50 – 2 × 37 = -24 (not possible) Hence, x = 8 is acceptable
∴ Length of pond = 50 – 2 × 8 = 34 m
Breadth of pond = 40 – 2 × 8 = 24 m

Question 5.
A car covers a distance of 2592 km with uniform speed. The number of hours taken for the journey is one-half the number representing the speed, in km/hour. Find the time taken to cover the distance.
Solution:
Let speed of the car be x km/h
According to question
Time taken = \(\frac{x}{2}\) h.

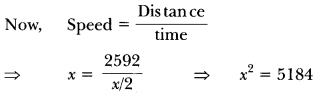
⇒ x = 72 km/h [Taking square root both sides]
∴ Time taken = \(\frac{x}{2}\) = 36 hours.