
On this page, you will find Quadratic Equations Class 10 Notes Maths Chapter 4 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 4 Quadratic Equations will seemingly help them to revise the important concepts in less time.
CBSE Class 10 Maths Chapter 4 Notes Quadratic Equations
Quadratic Equations Class 10 Notes Understanding the Lesson
1. Quadratic Equation: A quadratic equation in the variable x is of the form ax2 + bx + c = 0, where a, b, c are real number and a ≠ 0.
2. Roots (or zeroes of a quadratic equation): A real number a is called the root of the quadratic equation
ax2 + bx + c = 0 if aα2 + bα + c = 0.
Alternatively, any equation of the form p(x) = 0, where p(x) is a quadratic polynomial is a quadratic equation and if p(α) = 0 for any real number a; the a is said to be the root (or zero) of p(x).
Solution of a quadratic equation by factorization
Finding the roots of a quadratic equation by the method of factorization means finding out the linear factors of the quadratic equation and equating it to zero, the roots can be found. i.e. ax2 + bx + c = 0
(Ax + B) (Cr + D) = 0
where A, B, C and D are real numbers, A, C≠ 0.
We get Ax + B = 0 or Cx + D = 0
x =\(-\frac{B}{A}\) or x =\(-\frac{D}{C}\)
x =\(-\frac{\mathrm{B}}{\mathrm{A}},-\frac{\mathrm{D}}{\mathrm{C}}\) are the two roots of quadratic equation.
Solution of a quadratic equation by completing the square
For given quadratic equation ax2+ bx + c = 0
Divide the equation by a, so that the coefficient of x2 becomes 1.
\(x^{2}+\frac{b}{a} x+\frac{c}{a}=0\)
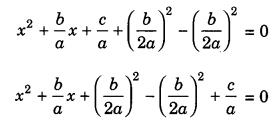
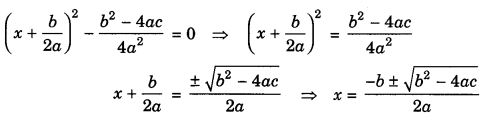
Adding and subtracting \(\left(\frac{b}{2 a}\right)^{2}\) i.e., square of the half of the coefficient of x.
This formula is known as quadratic formula.
If α and β are roots of the given equation, then
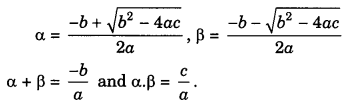
ax2 + bx + c = 0,
a ≠ 0, a, b, c ∈ R
Discriminant D = b2 – 4ac
Condition exists Nature of roots
(i) b2 – 4ac > 0 Real and unequal
(ii) b2 – 4ac = 0 Real and equal
(iii) b2 – 4ac < 0 No real roots