Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.
Quantum Mechanical Model of Atom – Schrodinger Equation:
The motion of objects that we come across in our daily life can be well described using classical mechanics which is based on the Newton’s laws of motion. In classical mechanics the physical state of the particle is defined by its position and momentum. If we know both these properties, we can predict the future state of the system based on the force acting on it using classical mechanics.
However, according to Heisenberg’s uncertainty principle both these properties cannot be measured simultaneously with absolute accuracy for a microscopic particle such as an electron. The classical mechanics does not consider the dual nature of the matter which is significant for microscopic particles.
As a consequence, it fails to explain the motion of microscopic particles. Based on the Heisenberg’s principle and the dual nature of the microscopic particles, a new mechanics called quantum mechanics was developed.
Erwin Schrodinger expressed the wave nature of electron in terms of a differential equation. This equation determines the change of wave function in space depending on the field of force in which the electron moves. The time independent Schrödinger equation can be expressed as,
\(\hat {H} \)Ψ = EΨ ………….. (2.12)
Where \(\hat {H} \) is called Hamiltonian operator, Ψ is the wave function and is a funciton of position Ψ(x, y, z) E is the energy of the system
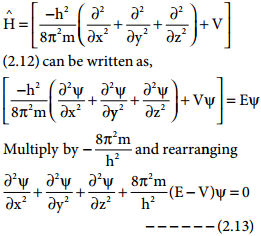
The above schrodinger wave equation does not contain time as a variable and is referred to as time independent Schrodinger wave equation. This equation can be solved only for certain values of E, the total energy. i.e. the energy of the system is quantised. The permitted total energy values are called eigen values and corresponding wave functions represent the atomic orbitals.
Main Features of the Quantum Mechanical Model of Atom
1. The energy of electrons in atoms is quantised
2. The existence of quantized electronic energy levels is a direct result of the wave like properties of electrons. The solutions of Schrodinger wave equation gives the allowed energy levels (orbits).
3. According to Heisenberg uncertainty principle, the exact position and momentum of an electron can not be determined with absolute accuracy. As a consequence, quantum mechanics introduced the concept of orbital. Orbital is a three dimensional space in which the probability of finding the electron is maximum.
4. The solution of Schrodinger wave equation for the allowed energies of an atom gives the wave function ψ, which represents an atomic orbital. The wave nature of electron present in an orbital can be well defined by the wave function ψ.
5. The wave function ψ itself has no physical meaning. However, the probability of finding the electron in a small volume dxdydz around a point (x, y, z) is proportional to |ψ(x, y, z)|<sup>2</sup> dxdydz around a point (x, y, z) is proportional to |ψ(x, y, z)|<sup>2</sup> is known as probability density and is always positive.