
On this page, you will find Rational Numbers Class 8 Notes Maths Chapter 1 Pdf free download. CBSE NCERT Class 8 Maths Notes Chapter 1 Rational Numbers will seemingly help them to revise the important concepts in less time.
CBSE Class 8 Maths Chapter 1 Notes Rational Numbers
Rational Numbers Class 8 Notes Conceptual Facts
1. A number which is in the form of \(\frac{p}{q}\), where p and q are co-primes integers and q ≠ 0 is called rational number.
For example, \(\frac{2}{3}, \frac{1}{2}, \frac{4}{5}, 2,-\frac{6}{7}\)
2. Every fraction is a rational number but every rational number need not to be a fraction.
For example: \(\frac{2}{3}\) is a fraction as well as a rational number, o
Whereas -5 is a rational number but it is not a fraction.
3. Standard form of a rational number may be identified when its denominator is positive.
For example: Standard form of is \(\frac{18}{-24} \text { is } \frac{-3}{4}\)
4. Equivalent fraction of \(\frac{p}{q}\) may be denoted by \(\frac{p \times m}{q \times m} \text { or } \frac{p \div n}{q \div n}\)
For example: Equivalent fractions of \(\frac{12}{16} \text { are } \frac{12+4}{16 \div 4}=\frac{3}{4}\)
or \(\frac{12 \times 2}{16 \times 2}=\frac{24}{32}\)
5. The rational numbers can be compared as:
- \(\frac{a}{b}>\frac{c}{d}\) if and only if ad > bc
- \(\frac{a}{b}=\frac{c}{d}\) if and only if ad = bc
- \(\frac{a}{b}<\frac{c}{d}\) if and only if ad < bc
Properties of rational numbers:
(а) Closure property additions
If a and b are two rational numbers, then a + b will also a rational number
For example: \(\frac{1}{2}+\frac{1}{3}=\frac{1 \times 3+1 \times 2}{6}=\frac{5}{6}\) a rational number.
(b) Commutative property of addition
Two rational numbers can be added in any manner.
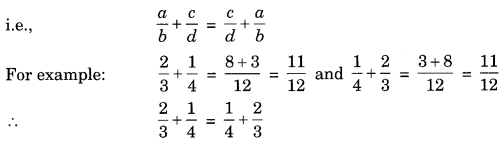
(c) Associative property for addition:
While adding three or more rational numbers, they can be grouped in any order.
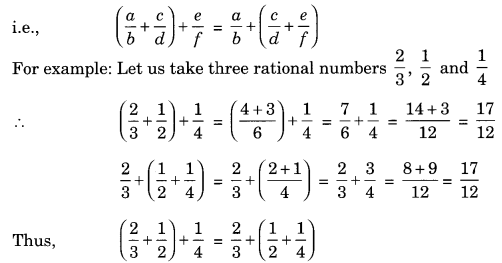
(d) Additive identity: The sum of any rational number and 0 is always equal to the rational number itself.
Zero is additive identity
For example: 0 + a = a or a + 0 = a
(e) Additive inverse
Additive inverse of \(\frac{a}{b}=-\frac{a}{b}\)
0 is the additive inverse of itself.
Properties of multiplication of rational numbers.
(a) Closure property: The product of two rational number is always a rational number.
For example: Take two rational numbers \(\frac{1}{2} \text { and } \frac{1}{3}\)
∴ \(\frac{1}{2} \times \frac{1}{3}=\frac{1}{6}\) which is also a rational numbers.
(b) Commutative property: The two rational numbers can be multiplied in any order,
i.e. a x b =b x a
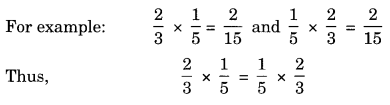
(c) Associative property: Three or more rational numbers can be multiplied by grouping in different order,
i.e. (a x b) x c = a x (b x c)
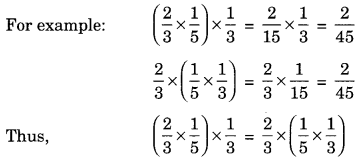
(d) Multiplicative identity: If \(\frac{a}{b}\) is a rational number, then \(\frac{a}{b} \times 1=1 \times \frac{a}{b}=\frac{a}{b}\)
For example: \(\frac{2}{3} \times 1=1 \times \frac{2}{3}=\frac{2}{3}\)
1 is called the multiplicative identity of a rational number.
(e) Distributive property of multiplication over addition.
If \(\frac{a}{b}, \frac{c}{d} \text { and } \frac{e}{f}\) are three rational number,
For example:
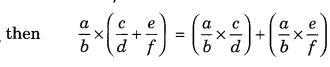
For example: Let us consider three rational numbers \(\frac{2}{3}, \frac{4}{5} \text { and } \frac{5}{6}\)
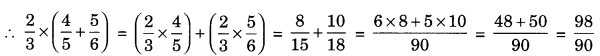
Existence of multiplicative inverse (i.e. Reciprocal)
For every non-zero rational number \(\frac{a}{b}\), there exists its multiplicative inverse \(\frac{a}{b}\).
- i.e… \(\frac{a}{b} \times \frac{b}{a}=1\)
- Reciprocal of zero (0) is not defined.
- 1 and -1 are the only two rational numbers which are Reciprocal of their own.
- Reciprocal of a reciprocal of a number is the number itself.
Representation of rational numbers on number line.

Here A represents \(\frac{1}{3}\) and B represents \(\frac{-2}{3}\) on the given number line.
Rational numbers between two given rational numbers:
Let us consider the rational numbers \(\frac{3}{10} \text { and } \frac{7}{10}\)
So, the rational numbers between \(\frac{3}{10} \text { and } \frac{7}{10} \text { may be } \frac{4}{10}, \frac{5}{10} \text { and } \frac{6}{10}\)