RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

Mark the correct alternative in each of the folloiwng :
Question 1.
If sec θ + tan θ = x, then sec θ =

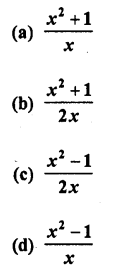
Solution:

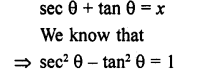
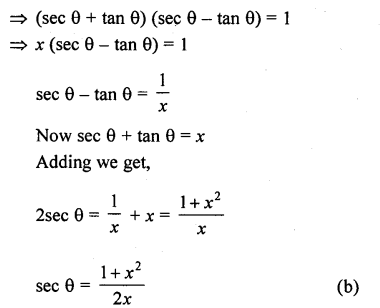
Question 2.

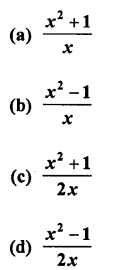
Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.
sec⁴ A – sec² A is equal to
(a) tan² A – tan⁴ A
(b) tan⁴ A – tan² A
(c) tan⁴ A + tan² A          
(d) tan² A + tan⁴ A
Solution:

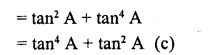
Question 6.
cos⁴ A – sin⁴ A is equal to
(a) 2 cos² A + 1        
(b) 2 cos² A – 1
(c) 2 sin² A – 1           
 (d) 2 sin² A + 1
Solution:
cos⁴ A – sin⁴ A = (cos² A + sin² A) (cos² A – sin² A)
= 1 (cos² A – sin² A) = cos² A – (1 – cos² A)
= cos² A – 1 + cos² A
= 2 cos² A – 1            (b)

Question 7.

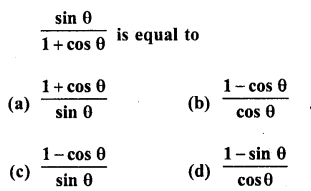
Solution:

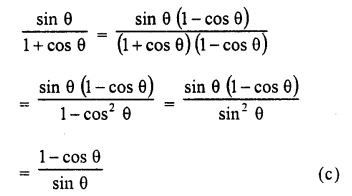
Question 8.

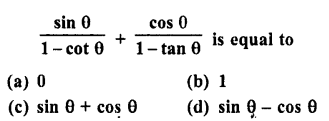
Solution:

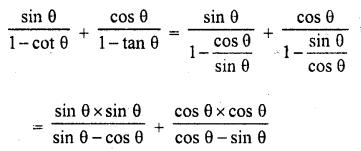
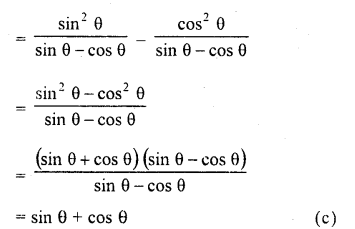
Question 9.
The value of (1 + cot θ – coscc θ) (1 + tan θ + sec θ) is
(a) 1                          
(b) 2
(c) 4                          
(d) 0
Solution:

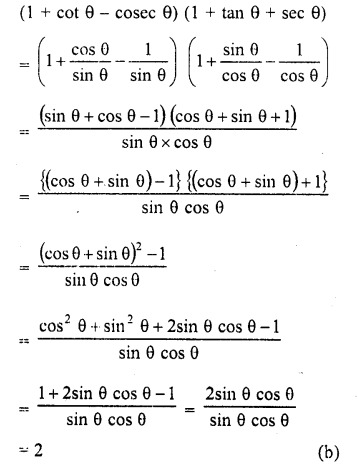
Question 10.

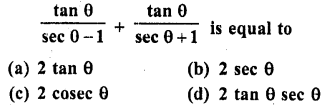
Solution:

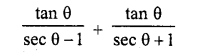
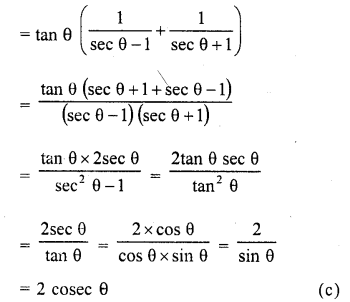
Question 11.
(cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ) is equal 
(a) 0                          
(b) 1
(c) -1
(d) None of these
Solution:

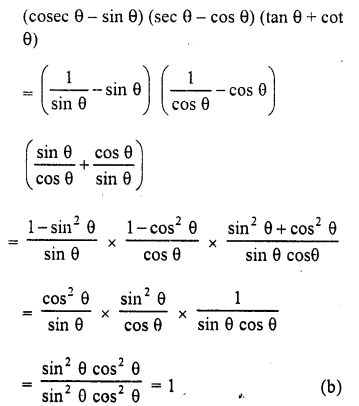
Question 12.
If x = a cos θ and y = b sin θ, then b²x² + a²y² =
(a) a²b²                             
(b) ab
(c) a⁴b⁴                      
(d) a² + b²
Solution:
x = a cos θ, y = b sin θ                       …(i)
bx = ab cos θ, ay = ab sin θ          ….(ii)
Adding (i) and (ii) we get,
b²x²+ a²y² = a²b² cos²  θ + a²b² sin²  θ
= a²b² (cos²  θ + sin²  θ)
= a²b² x 1
= a²b²                         (a)

Question 13.
If x = a sec θ and y-b tan θ, then b²x² – a²y²
(a) ab
(b) a² – b²
(c) a² + b²
(d) a²b²
Solution:
x = a sec θ and y = b tan θ
b²x² – a²y² = b² (a sec θ)² – a² (b tan θ)²
= a²b² sec² θ – a²b² tan²  θ
= a²b² (sec²  θ – tan²  θ)
= a²b² x 1
= a²b²                       (d)

Question 14.

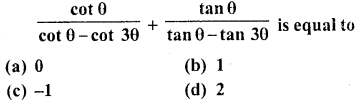
Solution:

Question 15.
2 (sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ) is equal to
(a) 0                
(b) 1
(c) -1               
(d) None of these
Solution:
.

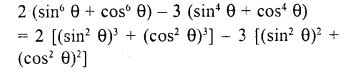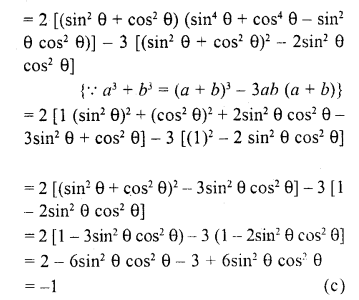
Question 16.
If a cos θ + b sin θ = 4 and a sin θ – b cos θ = 3, then a² + b² =
(a) 7                 
(b) 12
(c) 25                         
(d) None of these
Solution:
a cos θ + b sin θ = 4
a sin θ – b cos θ = 3
Squaring and adding
a² cos²  θ + b²  sin² θ  + 2ab sin θ cos θ=16
a² sin² θ + b²  cos² θ  – 2ab sin θ  cos θ = 9
a² (cos² θ + sin² θ) + b² (sin² θ + cos² θ) = 25 (∵ sin² θ + cos² θ=1)
⇒ a² x 1 + b² x 1 = 25
⇒  a² + b² = 25                                           (c)

Question 17.
If a cot θ + b cosec θ = p and b cot θ + a cosec θ = q, then p² – q² =
(a)   a² – b²                  
(b) b² – a²
(c)  a² + b²                  
(d)  b – a
Solution:
a cot θ + b cosec θ = p
b cot θ + a cosec θ = q
Squaring and subtracting,
p² – q²  = (a cot θ + b cosec θ)² – (b cot θ + a cosec θ)²
= a² cot² θ + b² cosec² θ + 2ab cot θ cosec θ – (b² cot² θ + a² cosec² θ + 2ab cot θ cosec θ)
= a² cot² θ +  b²  cosec² θ + lab cot θ cosec θ – b² cot²  θ – a² cosec² θ – lab cot θ cosec θ
= a² (cot² θ – cosec² θ) + b² (cosec² θ – cot^{2 θ})
= -a² (cosec² θ – cot² θ) + b² (cosec² θ – cot² θ)
= -a² x 1 + b² x 1 = b² – a²                                    (b)

Question 18.
The value of sin² 29° + sin² 61° is
(a) 1
(b) 0
(c) 2sin² 29“                 
(d)  2cos² 61°
Solution:
sin² 29° + sin² 61° = sin² 29° + sin² (99° – 29°)
= sin² 29 + cos² 29°              (a)
(sin² θ + cos² θ=1)

Question 19.
If x = r sin θ cos φ, y = r sin θ sin φ and z – r cos θ, then
(a) x² +y² + z² = r²      
(b)   x² +y² – z² = r²
(c) x²– y²+ z² = r²      
(d)   z² + y² – x² = r²
Solution:

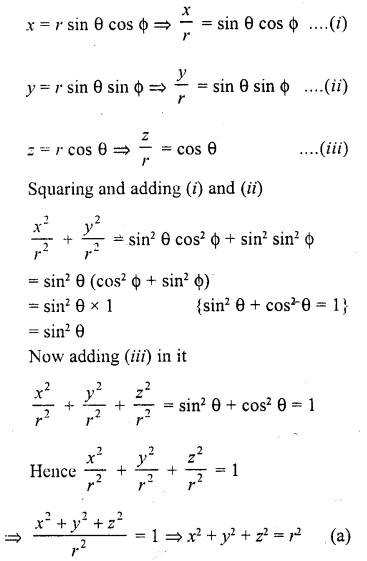
Question 20.
If sin θ + sin²  θ=1, then cos²  θ + cos⁴  θ
(a) -1                         
(b) 1
(c) 0                           
(d) None of these
Solution:
sin θ + sin² θ=1
⇒ sin θ = 1- sin² θ
⇒ sin θ = cos² θ
cos² θ + cos⁴ θ = sin θ + sin² θ     {∵ cos² θ = sin θ}
⇒  cos² θ + cos⁴ θ=1                                 (b)
{∵ sin θ + sin² θ = 1 (given)}

Question 21.
If a cos θ + b sin θ = m and a sin θ – b cos θ = it, then a² + b² =
(a) m² – it²        
(b) m²n²
(c) n² – m²        
(d) m² + n²
Solution:
a cos θ + b sin θ = m
a sin θ – b cos θ = n
Squaring and adding
a² cos² θ + b² sin² θ   + lab sin  θ cos θ = m²
a² sin² θ + b² cos² θ   – 2ab sin  θ cos θ = n²
a² (cos² θ + sin² θ) + b² (sin² θ + cos² θ) = m² + n²     {sin² θ + cos² θ=1}
⇒   a² + 1 + b² x 1 = m² – n²
⇒  a² + b² = m² + n²
Hence a² + b² = m² + n²          (d)

Question 22.
If cos A + cos² A = 1, then sin² A + sin⁴ A = 
(a) -1                         
(b) 0                            
(c) 1                           
(d) None of these
Solution:
cos A + cos² A = 1
⇒ cos A = 1 – cos² A
⇒  cos A = sin² A
Now, sin² A + sin⁴ A = cos A + cos² A = 1 (∵ cos A + cos² A = 1) (given)
∴ sin² A + sin⁴ A = 1                              (c)

Question 23.

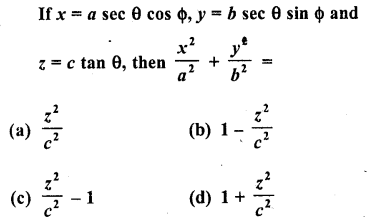
Solution:

Question 24.

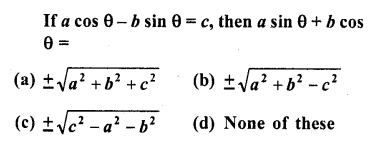
Solution:

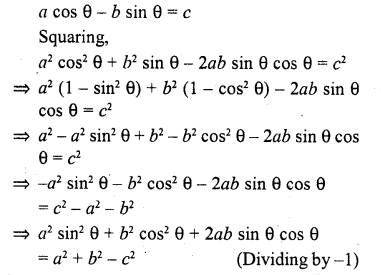
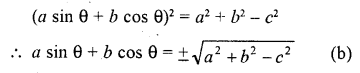
Question 25.
9sec² A – 9tan² A is equal to
(a) 1
(b) 9
(c) 8                           
(d) 0
Solution:
9sec² A – 9tan² A = 9 (sec² A – tan² A)
= 9 x 1       (∵ sec² A – tan² A = 1)
= 9                        (b)

Question 26.
(1 + tan θ + sec θ) (1 + cot θ – cosec θ) =
(a) 0
(b) 1
(c) 1                           
(d) -1
Solution:

Question 27.
(sec A + tan A) (1 – sin A) =
(a) sec A
(b) sin A
(c) cosec A                        
(d) cos A
Solution:

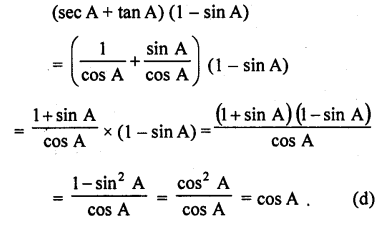
Question 28.

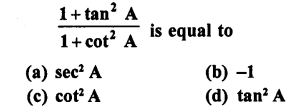
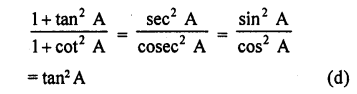
Question 29.
If sin θ cos θ = 0, then the value of sin⁴ θ + cos⁴ θ is

Solution:

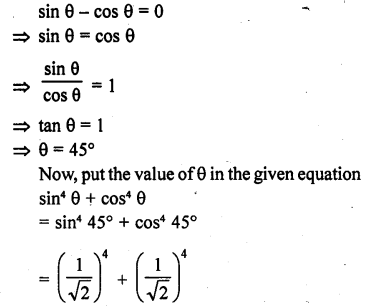
Question 30.
The value of sin (45° + θ) – cos (45° – θ) is equal to
(a) 2 cos θ                  
(b) 0
(c) 2 sin θ
(d) 1
Solution:
sin (45° + θ) – cos (45° – θ)
= sin (45° + θ) – sin (90° – 45° + θ)
= sin (45° + θ) – sift (45° + θ)
= 0                                                     (b)

Question 31.
If ΔABC is right angled at C, then the value of cos (A + B) is

Solution:

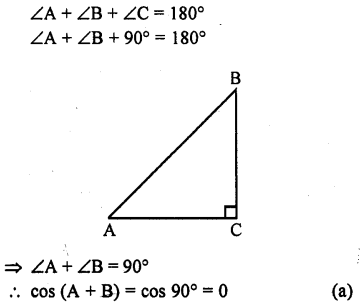
Question 32.

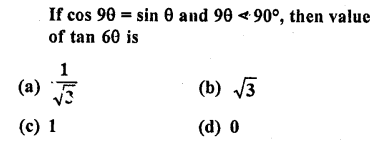
Solution:
cos (9θ) = sin θ
⇒ sin (90° – 9θ) = sin θ
⇒ 90° – 90 = θ
⇒ 9θ = 90°
⇒  θ= 10
tan 6θ = tan 6
= tan 60° = \(\sqrt { 3 } \)        (b)

Question 33.
If cos (α + β) =0 , then sin (α – β) can be reduced to 
(a) cos β
(b) cos 2β
(c) sin α
(d) sin 2α
Solution:
cos (α + β) = 0
⇒ α + β = 90°                       [∵ cos 90° = 0]
⇒  θ = 90° – β                                          …(i)
sin (α – β) = sin (90° – β – β) [using (i)]
= sin (90° – 2β)
= cos 2β [∵ sin (90° – θ) = cos θ]         (b)

Hope given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.