RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS

RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
Define an identity.
Solution:
An identity is an equation which is true for all values of the variable (s) involved.

Question 2.
What is the value of (1 – cos² θ) cosec² θ?
Solution:

Question 3.
What is the value of (1 + cot² θ) sin² θ ?
Solution:
(1 + cot² θ) sin² θ = cosec² sin² θ                           {1 + cot² θ = cosec² θ}
= (cosec θ sin θ)² = (l)² = 1                                      (∵ sin θ cosec θ=1)

Question 4.

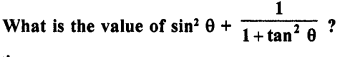
Solution:

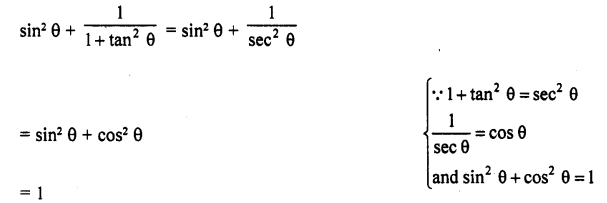
Question 5.
If sec θ + tan θ = x, write the value of sec θ – tan θ in terms of x.
Solution:
sec θ+ tan θ = x
We know that
sec² θ – tan² θ=1                                                                    .
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1                               {a² – b² = (a + b) (a – b)}
⇒  x (sec θ – tan θ) = 1
⇒  sec θ – tan θ = \(\frac { 1 }{ x }\)

Question 6.
If cosec θ – cot θ = α, write the value of cosec θ + cot α.
Solution:
cosec θ – cot θ = α
We know that,
cosec²  θ – cot²  θ=1
⇒  (cosec θ – cot θ) (cosec θ + cot θ) = 1
⇒  a (cosec θ + cot θ) = 1                                                {a² – b² = (a + b) (a – 6)}
⇒  cosec θ + cot θ = 1/α

Question 7.
Write the value of cosec² (90° – θ) – tan²θ
Solution:

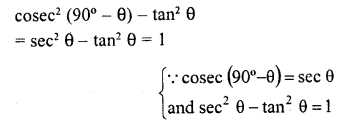
Question 8.
Write the value of sin A cos (90° – A) + cos A sin (90° – A)
Solution:

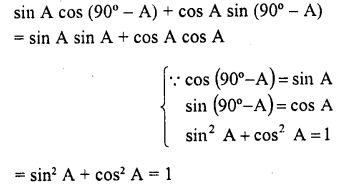
Question 9.

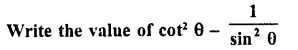
Solution:

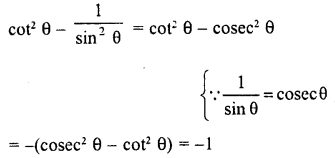
Question 10.
If x = a sin θ and y = b cos θ, what is the value of b²x² + a²y² ?
Solution:
x = a sin θ, y = b cos θ

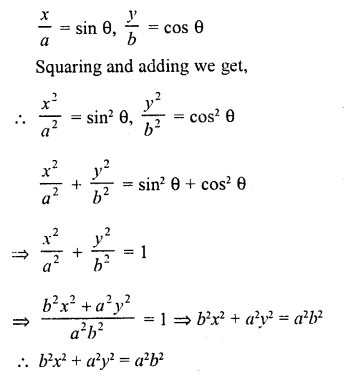
Question 11.
If sin θ = \(\frac { 4 }{ 5 }\), What is the value of cot θ + cosec θ ?
Solution:

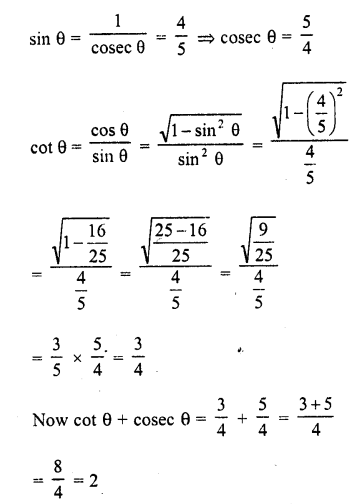
Question 12.
What is the value of 9 cot²  θ-9 cosec²  θ?
Solution:
9 cot²  θ – 9 cosec²  θ
= -(9cosec²  θ – 9cot²  θ)
= -9 (cosec²  θ – cot² θ) = -9 x 1
= -9                                                       {∵  cosec²  θ – cot² θ=1}

Question 13.

Solution:

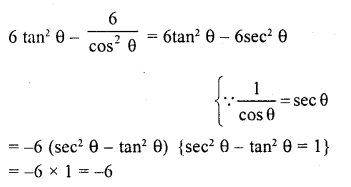
Question 14.

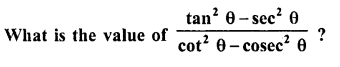
Solution:

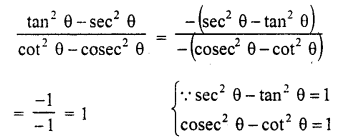
Question 15.
What is the value of (1 + tan² θ) (1 – sin θ) (1 + sin θ) ?
Solution:

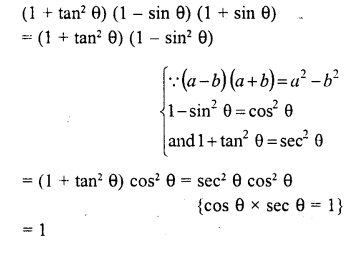
Question 16.
If cos A = \(\frac { 7 }{ 25 }\), find the value of tan A +cot A. (C.B.S.E. 2008)
Solution:

Question 17.
If sin θ = \(\frac { 1 }{ 3 }\), then find the value of 2 cot² θ + 2. (C.B.S.E. 2009)
Solution:

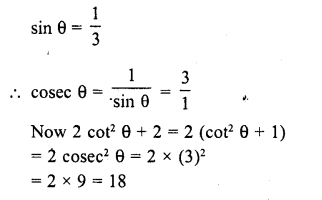
Question 18.
If cos θ = \(\frac { 3 }{ 4 }\), then find the value of 9 tan² θ + 9.
Solution:

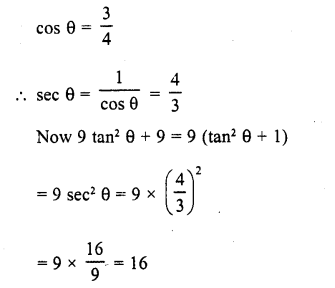
Question 19.
If sec²  θ (1 + sin θ) (1 – sin θ) = k, then find the value of k. (C.B.S.E. 2009)
Solution:

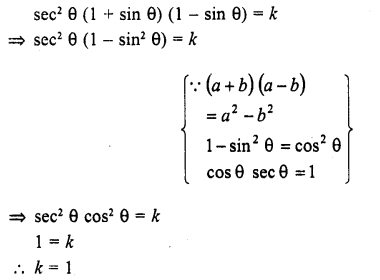
Question 20.
If cosec²  θ (1 + cos θ) (1 – cos θ) = λ, then find the value of λ.
Solution:
cosec²  θ (1 + cos θ) (1 – cos θ) = λ
⇒ cosec² θ (1 – cos² θ) = λ                      {(a + b) (a – b) = a¹ – b²)}
⇒  cosec² θ x sin θ = λ             (1 – cos² θ = sin² θ)
⇒ 1 = λ                                      (sin θ cosec θ=1)
∴ λ = 1

Question 21.
If sin² θ cos² θ (1 + tan² θ) (1 + cot² θ) = λ, then find the value of λ.
Solution:
sin² θ cos² θ (1+ tan² θ) (1 + cot² θ) = λ
sin² θ cos² θ (sec² θ) (cosec² θ) = λ

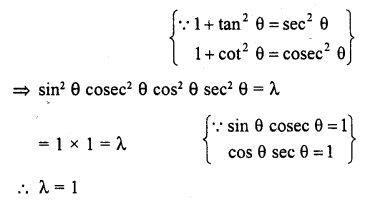
Question 22.


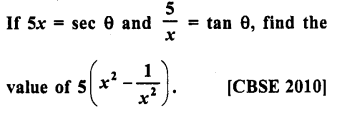
Solution:

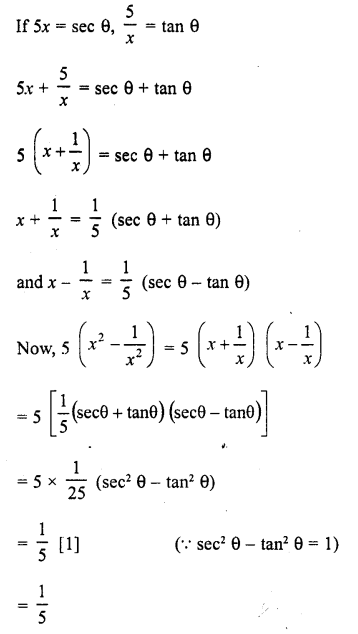
Question 23.
If cosec θ = 2x and cot θ = \(\frac { 2 }{ x }\), find the value of 2 ( x² – \(\frac { 1 }{ x2 }\)           [CBSE 2010]
Solution:

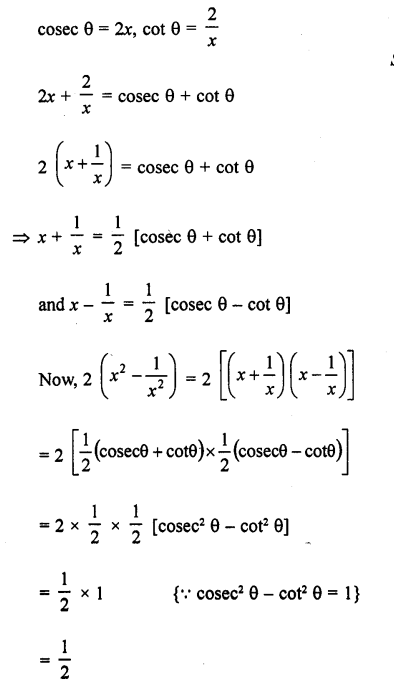
Question 24.
Write ‘True’ or ‘False’ and justify your answer in each of the following:
(i) The value of sin θ is x + \(\frac { 1 }{ x }\), where ‘x’ is a positive real number.
(ii) cos θ = \(\frac { { a }^{ 2 }+{ b }^{ 2 } }{ 2ab }\) , where a and b are two lab distinct numbers such that ab > 0.
(iii) The value of cos² 23 – sin² 67 is positive.
(iv) The value of the expression sin 80° – cos 80° is negative.
(v) The value of sin θ + cos θ is always greater than 1.
Solution:

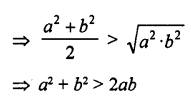
Hope given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.