RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS
Other Exercises
- RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1
- RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS
- RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS
Mark the correct alternative in each of the following :
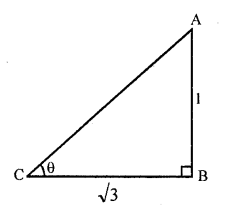
Question 1.
The ratio of the length of a rod and its shadow is 1 : \(\sqrt { 3 } \) The angle of elevation of the sum is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution:
Let AB be rod and BC be its shadow
So that AB : BC = 1 : \(\sqrt { 3 } \)
Let θ be the angle of elevation
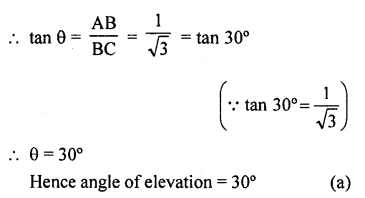
Question 2.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60?, the height of the tower is

Solution:
Let AB be the tower and a point P at a distance of 100 m from its foot, angle of elevation of the top of the tower is 60°
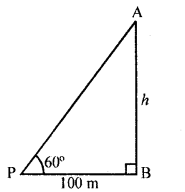
Let height of the tower = h

Question 3.
If the altitude of the sun is at 60?, then the height of the vertical tower that will cast a shadow of length 30 m is
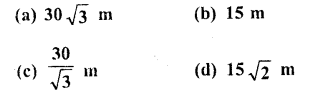
Solution:
Let AB be tower and a point P distance of 30 m from its foot of the tower which form an angle of elevation pf the sun of 60°
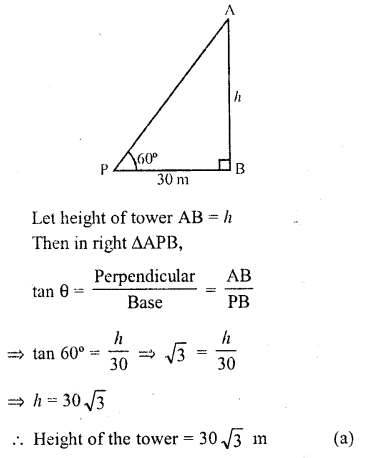
Question 4.
If the angles of elevation of a tower from two points distance a and b (a > b) from its foot and in the same straight line from it are 30? and 60?, then the height of the tower is
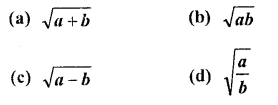
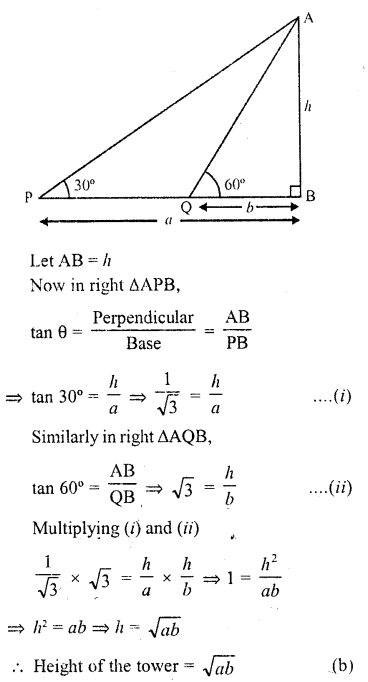
Solution:
Let AB be the tower and P and Q are such points that PB = a, QB = b and angles of elevation at P and Q are 30° and 60° respectively
Question 5.
If the anglr of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with It are complementary, then the height of the tower is

Solution:
Let AB be the tower and P and Q are two points such that PB = a and QB = b and angles of elevation are θ and (90° – θ)
Let height of tower = h
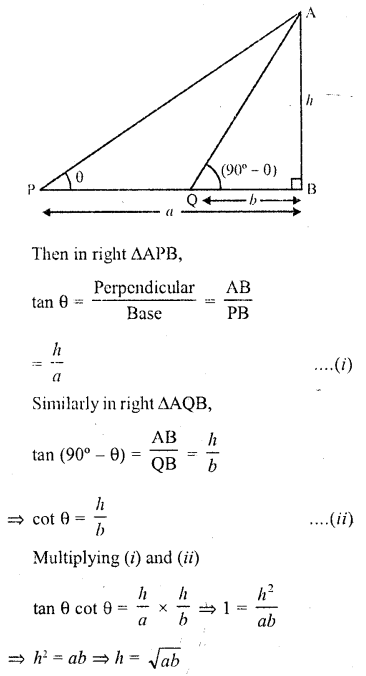
![]()
Question 6.
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
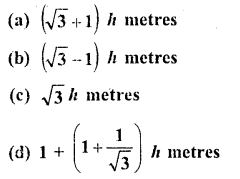
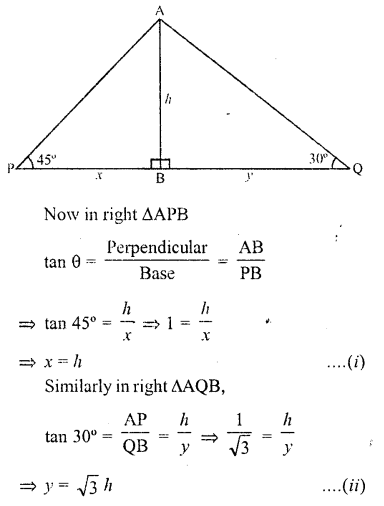
Solution:
Let AB be light house and P and Q are two ships on its opposite sides which form angle of elevation of A as 45° and 30° respectively AB = h
Let PB = x and QB = y
Question 7.
The angle of elevation of the top of a tower stahding on a horizontal plane from a point A is a. After walking a distance d towards the foot of the tower the angle of elevation is found to be p. The height of the tower is
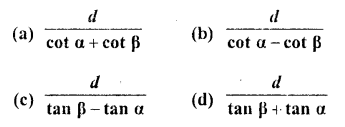
Solution:
Let AB be the tower and C is a point such that the angle of elevation of A is a. After walking towards the foot B of the tower, at D the angle of elevation is p Let h be the height of the tower and DB = x Now in right AACB,
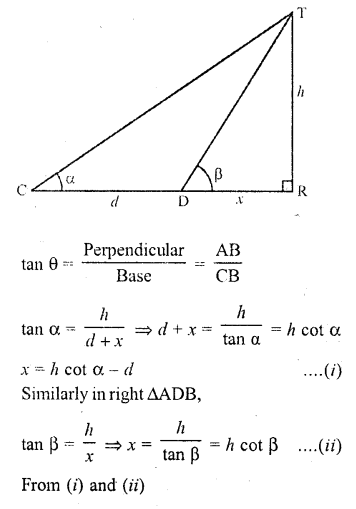
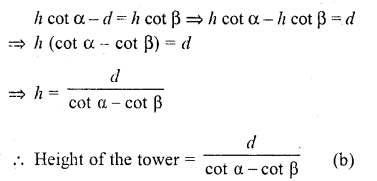
Question 8.
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
(a) 12 m
(b) 10 in
(c) 8 m
(d) 6 m
Solution:
Let AB and CD be two poles
AB = 20 m, CD = 14 m
A and C are joined by a wire
CE || DB and angle of elevation of A is 30° Class 10 Solutions Chapter 12 Heights and Distances MCQS – 9.png
Let CE = DB = x and AC = l
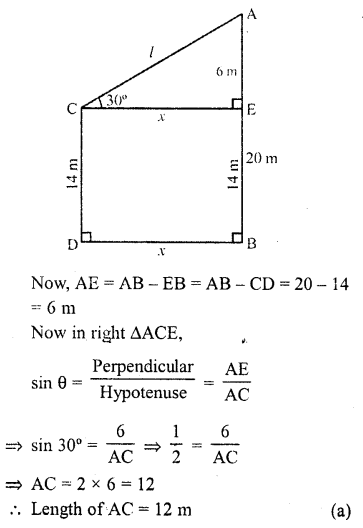
Question 9.
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
(a) 25 m
(b) 50 in
(c) 75 m
(d) 100 m
Solution:
Let AB be the tower and CD be cliff Angle of elevation of A is equal to the angle of depression of B at C
Let angle be Q and CD = 25 m
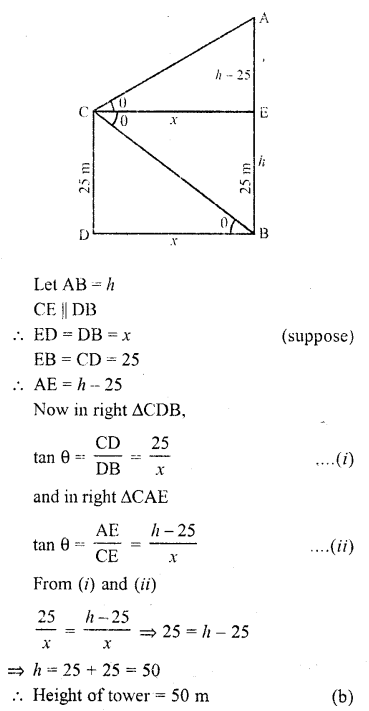
Question 10.
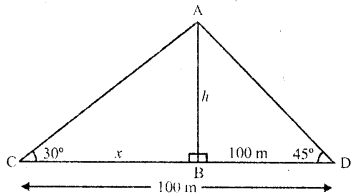
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart, the height of the light house is
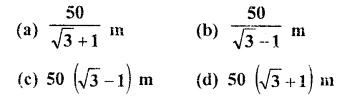
Solution:
Let AB be the light house C and D are two ships whose angles of depression on A are 30° and 45° respectively
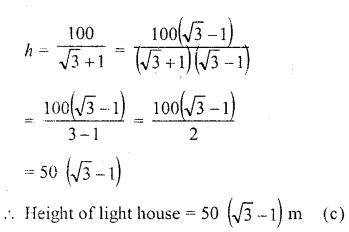

Question 11.
if the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake, is
(a) 200 m
(b) 500 m
(c) 30 m
(d) 400 m
Solution:
Let C be the cloud and R is its reflection in the lake
L is a point 200 m above the lake. Such that
LM = 200 m
Angle of elevation of C with L is 30° and angle of depression of R is 60°
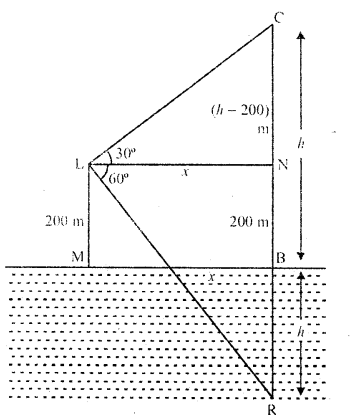
Let height of cloud CB = h
∴ BR = h and NB = LM = 200 m
∴ CN = (h – 200) m and NR = (h + 200) m

Question 12.
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
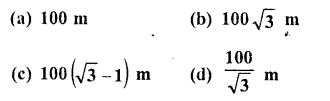
Solution:
Let AB be tower and AB = 100 m and angles of elevation of A at C and D are 30° and 45° respectively and CD = x
Let BD =y
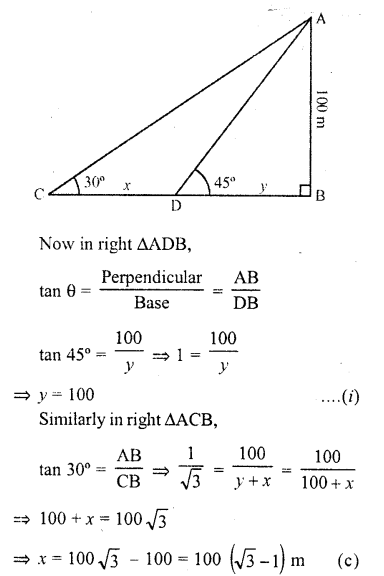
Question 13.
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is

Solution:
Let AB and CD are two persons standing ‘a’ metres apart
M is the mid-point of BD and from M, the angles of elevation of A and C are complementary

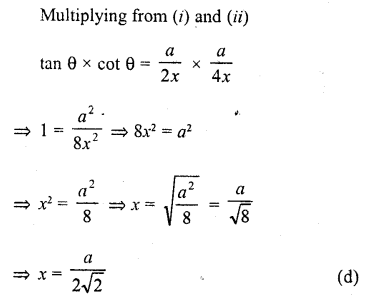
Question 14.
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
(a) It tan (45° + θ)
(b) h cot (45° – θ)
(c) h tan (45° – θ)
(d) h cot (45° + θ)
Solution:
Let C is the cloud and R is its reflection in the lake
From the lake, ‘7’ m aboves it, E is point
where angle of elevation of C is θ
and angle of depression of reflection is 45°
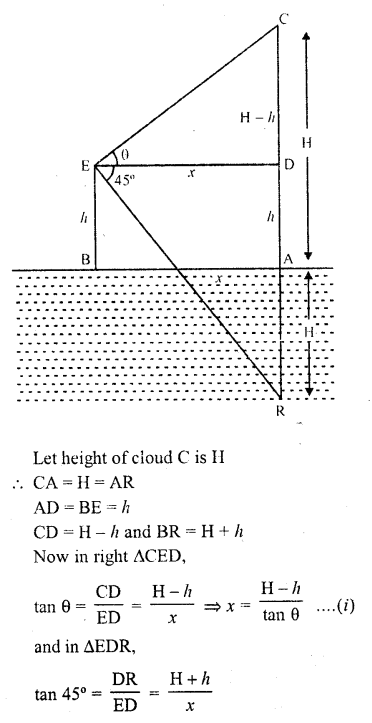

Question 15.
A lower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is

Solution:
Let CD is the tower and A is a point such that the angle of elevation of C is 30°
B is and their point h m high of A and angle of depressio of D is 60°
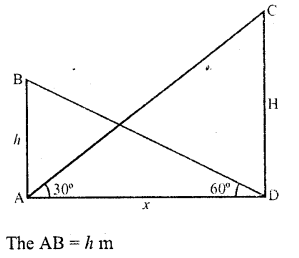

Question 16.
It is found that on walking x metres towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60° . The height of the chimney is
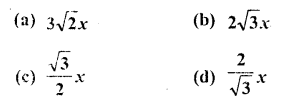
Solution:
In the figure, AB is chimney and CB and DB are its shadow
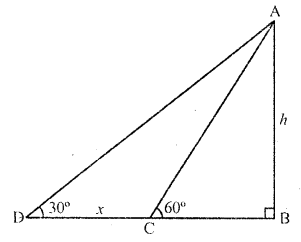
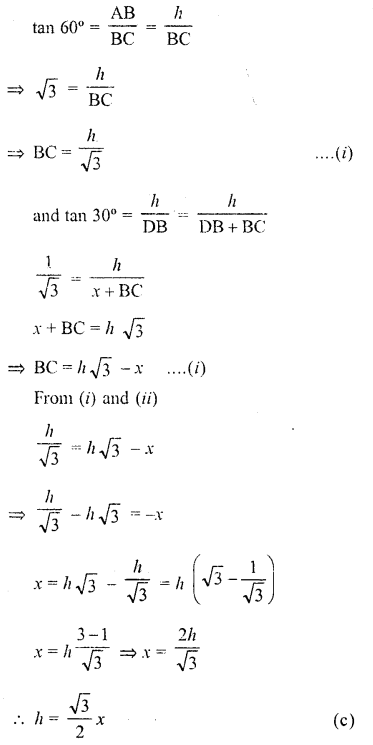
Question 17.
The length of the shadow of a tower standing on level ground is found to be 2.v metres longer when the sun’s elevation is 30° than when it was 45° . The height of the tower in metres is
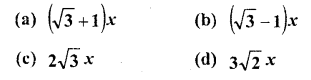
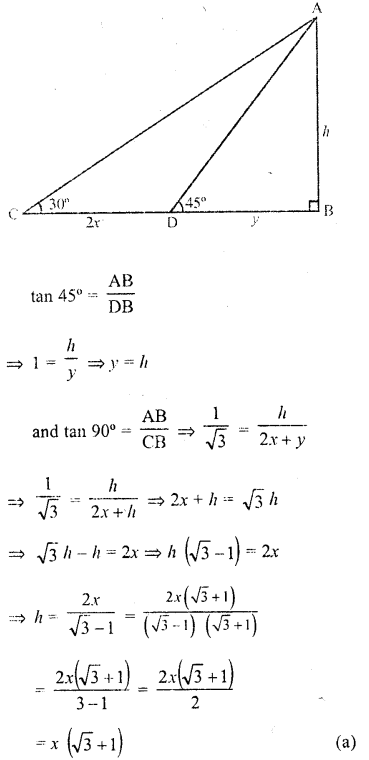
Solution:
AB is a tower
BD and BC are its shadows and CD = 2x
Question 18.
Two poles are ‘a’ metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
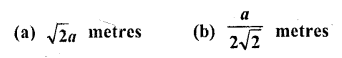

Solution:
Let height of pole CD = h
and AB = 2h, BD = a
M is mid-point of BD

Question 19.
The tops of two poles of height 16 m and 10 m are connected by a wire of length l metres. If the wire makes an angle of 30° with the horizontal, then l =
(a) 26
(b) 16
(c) 12
(d) 10
Solution:
Let AB and CD are two poles AB = 10 m and CD = 16 m
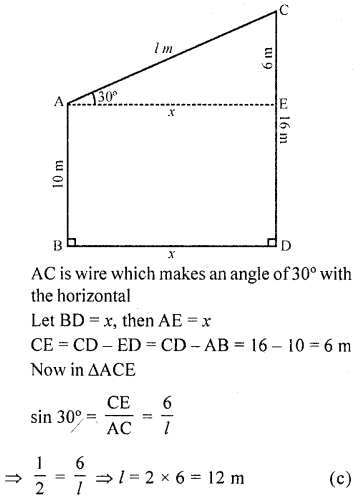
Question 20.
If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
(a) 1.5 m
(b) 2 m
(c) 2.5 m
(d) 2.8 m
Solution:
Let AB is girls and CD is lamp-post AB = 1.5
which casts her shadow EB
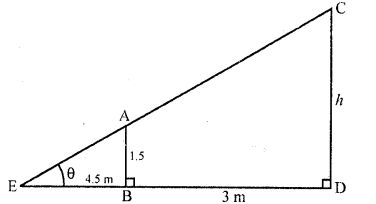

Question 21.
The length of shadow of a tower on the plane ground is \(\sqrt { 3 } \) times the height of the tower. The angle of elevation of sun is
(a) 45°
(b) 30°
(c) 60°
(d) 90° [CBSE 2012]
Solution:
Let AB be tower and BC be its shadow
∴Let AB = x
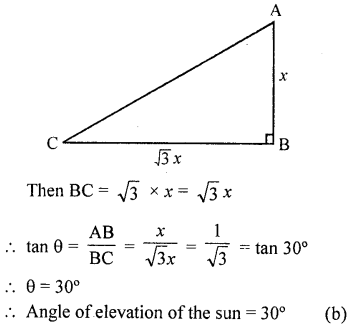
Question 22.
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
(a) 25 \(\sqrt { 3 } \)
(b) 50 \(\sqrt { 3 } \)
(c) 75 \(\sqrt { 3 } \)
(d) 150 [CBSE 2013]
Solution:
AB is a tower and AB = 75 m
From A, the angle of depression of a car C
on the ground is 30°
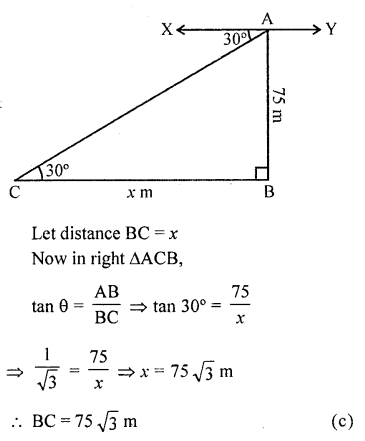
Question 23.
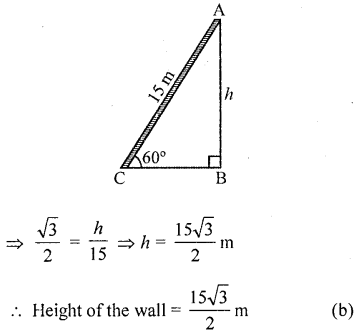
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
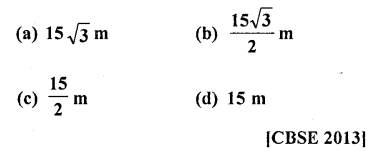
Solution:
Let AB is a wall and AC is the ladder 15 m long which makes an angle of 60° with the ground
∴In ∆ABC, ∠B = 90°
Let height of wall AB = h
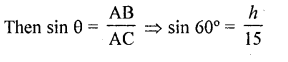
Question 24.
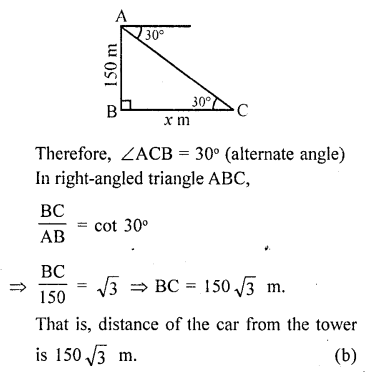
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
(a) 50\(\sqrt { 3 } \)
(b) 150 \(\sqrt { 3 } \)
(c) 150 \(\sqrt { 3 } \)
(d) 75
Solution:
Let AB be the tower of height 150 m
C is car and angle of depression is 30°
Question 25.
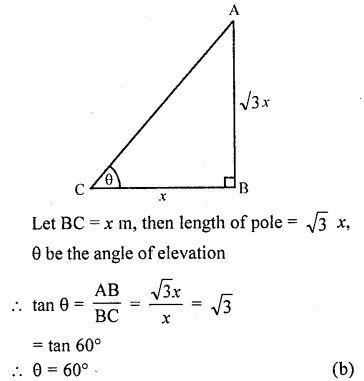
If the hei8ht of a vertical pole is \(\sqrt { 3 } \) times the length of its shadow on the ground, then the angle of elevation of the sun at that time is
(a) 30°
(b) 60°
(c) 45°
(d) 75° [CBSE 2014]
Solution:
Let AB be a vertical pole and let its shadow be BC
Question 26.
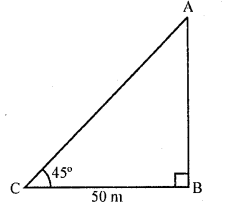
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45°. Then the height of the tower (in metres) is
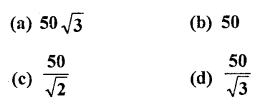
Solution:
Let AB be tower and C is a point on the ground 50 m away

Question 27.
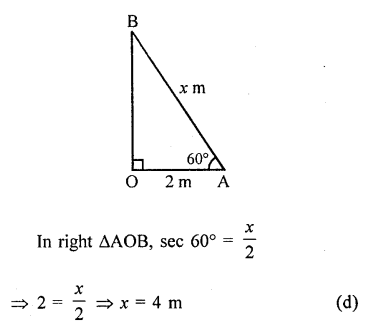
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is

Solution:
Suppose AB is the ladder of length x m
∴ OA = 2m, ∠OAB = 60°
Hope given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.