RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6
Other Exercises
- RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.1
- RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.2
- RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.3
- RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.4
- RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.5
- RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6
- RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.7
- RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.8
Question 1.
Verify the property : x x y = y x x by taking :
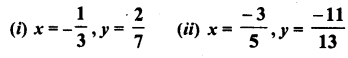
Solution:
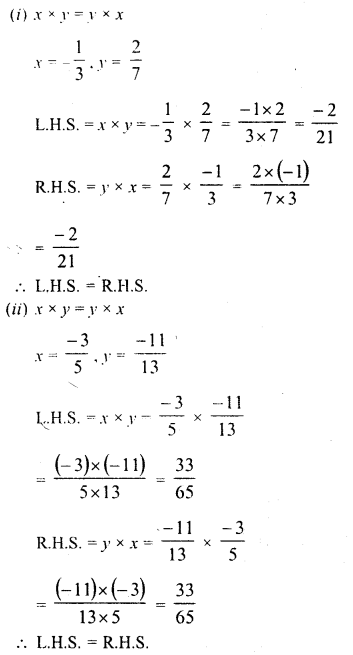
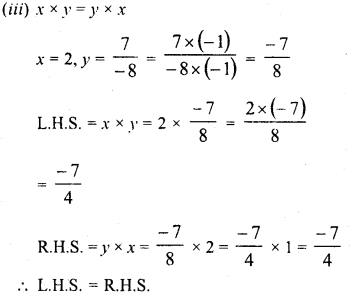
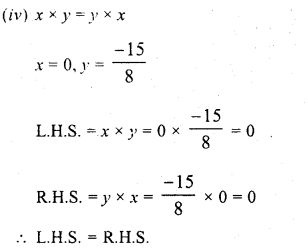
Question 2.
Verify the property : x x (y x z) = (x x y) x z by taking :
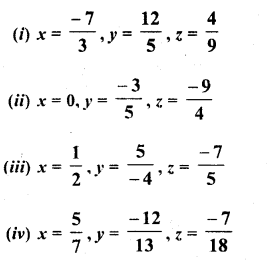
Solution:
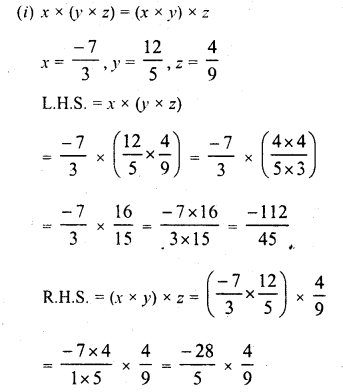
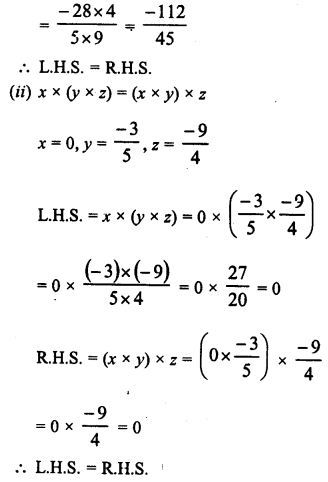
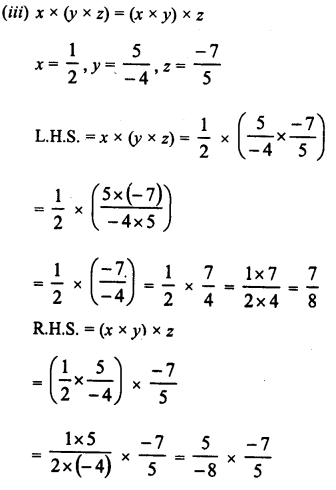
Question 3.
Verify the property :xx(y + 2) = xxy + x x z by taking :
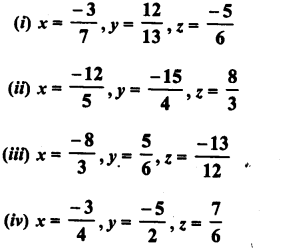
Solution:
![]()
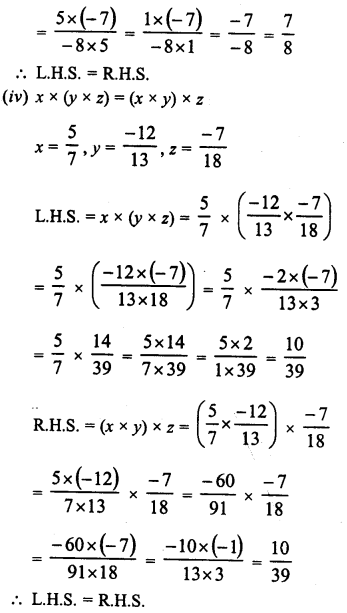
Question 4.
Use the distributivity of multiplication of rational numbers over their addition to simplify :
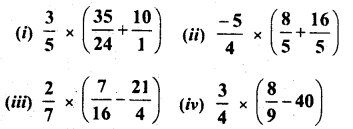
Solution:
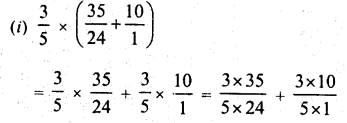
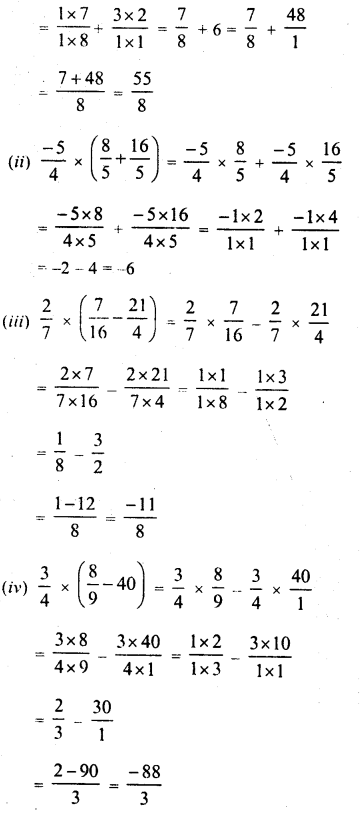
Question 5.
Find the multiplicative inverse (reciprocal) of each of the following rational numbers :

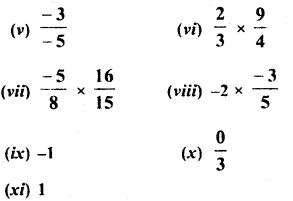
Solution:


Question 6.
Name the property of multiplication of rational numbers illustrated by the following statements :
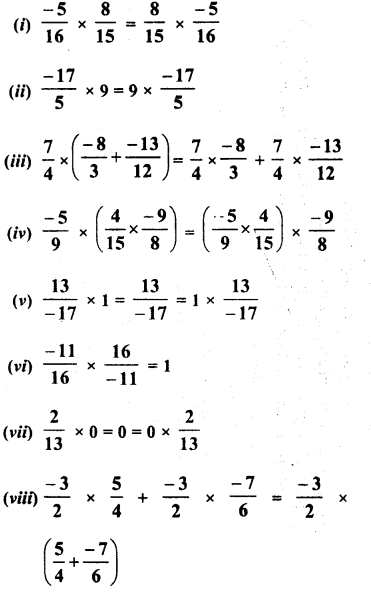
Solution:
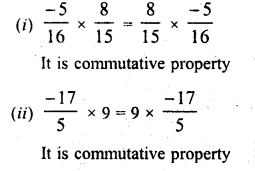

Question 7.
(i) The product of two positive rational numbers is always______.
(ii) The product of a positive rational number and a negative rational number is always________.
(iii) The product of two negative rational numbers is always________.
(iv) The reciprocal of a positive rational number is________.
(v) The reciprocal of a negative rational number is________.
(vi) Zero has reciprocal. The product of a rational number and its reciprocal is______.
(viii) The numbers and are their own reciprocals______.
(ix) If a is reciprocal of b, then the reciprocal of b is______.
(x) The number 0 is the reciprocal of any number______.
(xi) Reciprocal of \(\frac { 1 }{ a }\), a≠ 0 is______.
(xii) (17 x 12)-1 = 17-1 x________ .
Solution:
The product of two positive rational numbers is always positive.
(ii) The product of a positive rational number and a negative rational number is always negative.
(iii) The product of two negative rational numbers is always positive.
(iv) The reciprocal of a positive rational number is positive.
(v) The reciprocal of a negative rational number is negative.
(vi) Zero has no reciprocal.
(vii) The product of a rational number and its reciprocal is 1.
(viii)The numbers 1 and -1 are their own reciprocals.
(ix) If a is reciprocal of b, then the reciprocal of b is a.
(x) The number 0 is not the reciprocal of any number.
(xi) Reciprocal of \(\frac { 1 }{ a }\), a≠ 0 is a.
(xii) (17 x 12)-1 = 17-1 x________ .
Question 8.
Fill in the blanks :
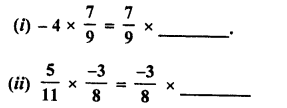
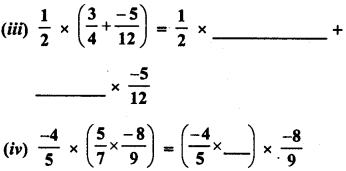
Solution:
Fill in the blanks :
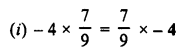
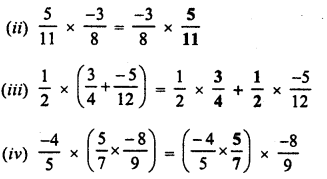
Hope given RD Sharma Class 8 Solutions Chapter 1 Rational Numbers Ex 1.6 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.