RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
Other Exercises
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9
Question 1.
Find the squares of the following numbers using column method. Verify the result by finding the square using the usual multiplication :
(i) 25
(ii) 37
(iii) 54
(iv) 71
(v) 96
Solution:
(i) (25)2
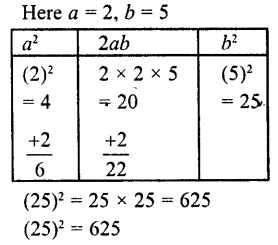

Question 2.
Find the squares of the following numbers using diagonal method :
(i) 98
(ii) 273
(iii) 348
(iv) 295
(v) 171
Solution:
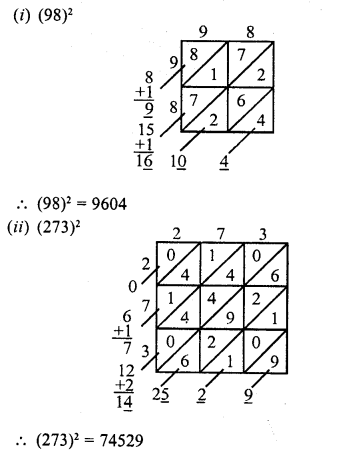
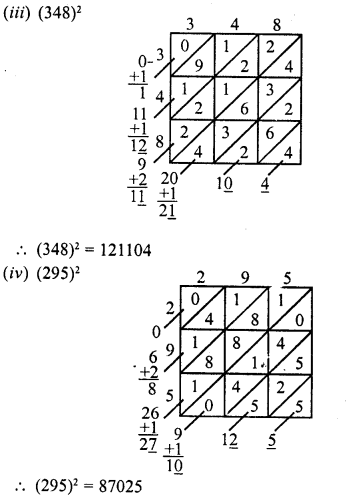
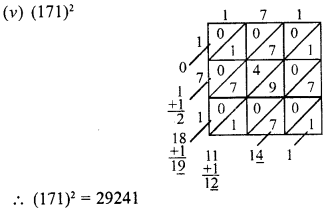
Question 3.
Find the squares of the following numbers :
(i) 127
(ii) 503
(iii) 451
(iv) 862
(v) 265
Solution:
(i) (127)2 = (120 + 7)2
{(a + b)2 = a2 + lab + b2}
= (120)2 + 2 x 120 x 7 + (7)2
= 14400+ 1680 + 49 = 16129
(ii) (503)2 = (500 + 3)2
{(a + b)2 = a2 + lab + b1}
= (500)2 + 2 x 500 x 3 + (3)2
= 250000 + 3000 + 9 = 353009
(iii) (451)2 = (400 + 51)2
{(a + b)2 = a2 + lab + b2}
= (400)2 + 2 x 400 x 51 + (5l)2
= 160000 + 40800 + 2601 = 203401
(iv) (451)2 = (800 + 62)2
{(a + b)2 = a2 + lab + b2}
= (800)2 + 2 x 800 x 62 + (62)2
= 640000 + 99200 + 3844 = 743044
(v) (265)2
{(a + b)2 = a2 + 2ab + b2}
(200 + 65)2 = (200)2 + 2 x 200 x 65 + (65)2
= 40000 + 26000 + 4225 = 70225
Question 4.
Find the squares of the following numbers
(i) 425
(ii) 575
(iii) 405
(iv) 205
(v) 95
(vi) 745
(vii) 512
(viii) 995
Solution:
(i) (425)2
Here n = 42
∴ n (n + 1) = 42 (42 + 1) = 42 x 43 = 1806
∴ (425)2 = 180625
(ii) (575)2
Here n = 57
∴ n (n + 1) = 57 (57 + 1) = 57 x 58 = 3306
∴ (575)2 = 330625
(iii) (405)2
Here n = 40
∴ n (n + 1) = 40 (40 + 1) -40 x 41 = 1640
∴ (405)2 = 164025
(iv) (205)2
Here n = 20
∴ n (n + 1) = 20 (20 + 1) = 20 x 21 = 420
∴ (205)2 = 42025
(v) (95)2
Here n = 9
∴ n (n + 1) = 9 (9 + 1) = 9 x 10 = 90
∴ (95)2 = 9025
(vi) (745)2
Here n = 74
∴ n (n + 1) = 74 (74 + 1) = 74 x 75 = 5550
∴ (745)2 = 555025
(vii) (512)2
Here a = 1, b = 2
∴ (5ab)2 = (250 + ab) x 1000 + (ab)2
∴ (512)2 = (250 + 12) x 1000 + (12)2
= 262 x 1000 + 144
= 262000 + 144 = 262144
(viii) (995)2
Here n = 99
∴ n (n + 1) = 99 (99 + 1) = 99 x 100 = 9900
∴ (995)2 = 990025
Question 5.
Find the squares of the following numbers using the identity (a + b)1 = a2 + lab + b1
(i) 405
(ii) 510
(iii) 1001
(iv) 209
(v) 605
Solution:
a + b)2 = a2 + lab + b2
(i) (405)2 = (400 + 5)2
= (400)2 + 2 x 400 x 5 + (5)2
= 160000 + 4000 + 25 = 164025
(ii) (510)2 = (500 + 10)2
= (500)2 + 2 x 500 x 10 x (10)2
= 250000 + 10000 + 100
= 260100
(iii) (1001)2 = (1000+1)2
= (1000)2 + 2 X 1000 x 1 + (1)
= 1000000 + 2000 + 1
=1002001
(iv) (209)2 = (200 + 9)2
= (200)2 + 2 x 200 x 9 x (9)2
= 40000 + 3600 +81
= 43681
(v) (605)2 = (600 + 5)2
= (600)2 + 2 x 600 x 5 +(5)2
= 360000 + 6000 25
=366025
Question 6.
Find the squares of the following numbers using the identity (a – b)2 = a2 – 2ab + b2 :
(i) 395
(ii) 995
(iii) 495
(iv) 498
(v) 99
(vi) 999
(vii) 599
Solution:
a – b)2 = a2 – lab + b2
(i) (395)2 = (400 – 5)2
= (400)2 – 2 x 400 x 5 + (5)2
= 160000-4000 + 25
= 160025-4000
= 156025
(ii) (995)2 = (1000 – 5)2
= (1000)2 – 2 x 1000 x 5 + (5)2
= 1000000- 10000 + 25
= 1000025- 10000
= 990025
(iii) (495)2 = (500 – 5)2
= (500)2 – 2 x 500 x 5 + (5)2
= 250000 – 5000 + 25
= 250025 – 5000
= 245025
(iv) (498)2 = (500 – 2)2
= (500)2 – 2 x 500 x 2 + (2)2
= 250000 – 2000 + 4
= 250004 – 2000
= 248004
(v) (99)2 = (100 – l)2
= (100)2 – 2 x 100 x 1 + (1)2
= 10000 – 200 + 1
= 10001 – 200
= 9801
(vi) (999)2 = (1000- l)2
= (1000)2 – 2 x 1000 x 1+ (1)2
= 1000000-2000+1
= 10000001-2000=998001
(vii) (599)2 = (600 – 1)2
= (600)2 -2 x 600 X 1+ (1)2
= 360000 -1200+1
= 360001 – 1200 = 358801
Question 7.
Find the squares of the following numbers by visual method :
(i) 52
(ii) 95
(iii) 505
(iv) 702
(v) 99
Solution:
(a + b)2 = a2 – ab + ab + b2
(i) (52)2 = (50 + 2)2
= 2500 + 100 + 100 + 4
= 2704
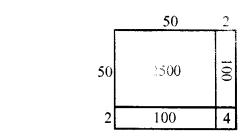
(ii) (95)2 = (90 + 5)2
= 8100 + 450 + 450 + 25
= 9025
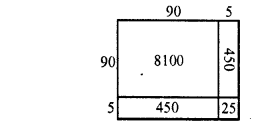
(iii) (505)2 = (500 + 5)2
= 250000 + 2500 + 2500 + 25
= 255025
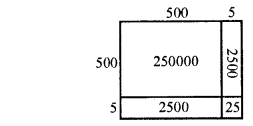
(iv) (702)2 = (700 + 2)2
= 490000 + 1400+ 1400 + 4
= 492804
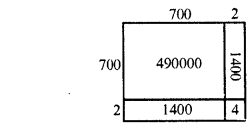
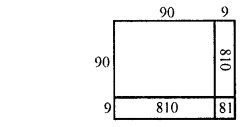
(v) (99)2 = (90 + 9)2
= 8100 + 810 + 810 + 81
= 9801
Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.