RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5

Other Exercises

• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.1
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.2
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.3
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.4
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6
• RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.7

Multiply:

Question 1.
(5x + 3) by (7x + 2)
Solution:
(5x + 3) x (7x + 2)
= 5x (7x + 2) + 3 (7x + 2)
= 35x² + 10x + 21x + 6
= 35x² + 31x + 6

Question 2.
(2x + 8) by (x – 3)
Solution:
(2x + 8) x (x – 3)
= 2x (x – 3) + 8 (x – 3)
= 2x² – 6x + 8x – 24
= 2x² + 2x – 24

Question 3.
(7x +y) by (x + 5y)
Solution:
(7x + y) x (x + 5y)
= 7x (x + 5y) + y (x + 5y)
= 7x² + 35xy + xy + 5y²
=7x² + 36xy + 5y²

Question 4.
(a – 1) by (0.1a² + 3)
Solution:
(a – 1) x (0.1a² + 3)
= a (0.1a² + 3) – 1 (0.1a²+ 3)
= 0.1a³ + 3a-0.1a²-3
= 0.1a³ – 0.1a² + 3a-3

Question 5.
(3x² +y²) by (2x² + 3y²)
Solution:
(3x²+y²) x (2x² + 3y²)
= 3x² (2x² + 3y²) + y²(2x² + 3y²)
= 6x^{2 +2} + 9x²y² + 2x²y² + 3y^{2 + 2}
= 6x⁴ + 11 x²y² + 3y⁴

Question 6.

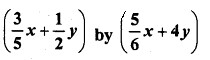
Solution:

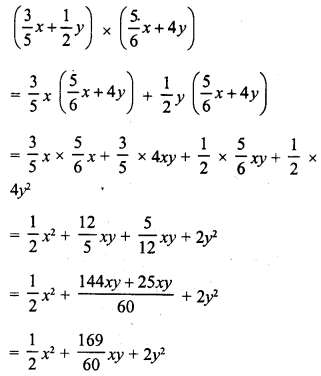
Question 7.
(x⁶-y⁶) by (x²+y²)
Solution:
(x⁶ – y⁶) x (x² + y²)
= x⁶ (x² + y²) – y⁶ (x² + y²)
= x⁶ x x² + x⁶y² – x²y⁶ -y⁶ x y²
= x^{6 + 2} + x⁶y² – x²y⁶ – y^{6 +2}
= x  + x⁶y² – x²y⁶ – y⁸

Question 8.
(x² + y²) by (3a+2b)
Solution:
(x² + y²) x (3a + 2b)
= x² (3a + 2b) + y² (3a + 2b)
= 3x²a + 2x²b + 3y²a + 2y²b
3ax² + 3av² + 2bx² + 2by²

Question 9.
[-3d + (-7ƒ)] by (5d +ƒ)
Solution:
[-3d + (-7ƒ)] x (5d +ƒ)
= -3d x (5d +ƒ) + (-7ƒ) x (5d +ƒ)
= -15d²-3dƒ- 35dƒ- 7ƒ²
= -15d² – 38dƒ- 7ƒ²

Question 10.
(0.8a – 0.5b) by (1.5a -3b)
Solution:
(0.8a – 0.5b) x (1.5a-3b)
= 0.8a x (1.5a – 36) – 0.56 (1.5a -3b)
= 1.2a² – 2.4ab – 0.75ab + 1.5b²
= 1.2a²-3.15ab+ 1.5b²

Question 11.
(2x² y² – 5xy²) by (x² -y²)
Solution:
(2x² y² – 5xy²) x (x² -y²)
= 2x²y² (x² – y²) – 5x_y² (x² – y²)
= 2x²y² x x² – 2x²y² xy²– 5xy² x x² + 5x² xy²
= 2x^{2 + 2} y²– 2x² x y^{2 + 2}– 5x¹⁺² y²+5xy^{2 + 2}
= 2x⁴y²– 2x²y⁴ – 5x³y²+ 5xy⁴

Question 12.

Solution:

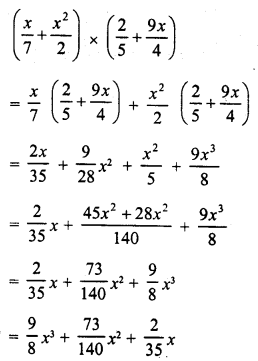
Question 13.

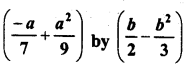
Solution:

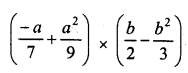
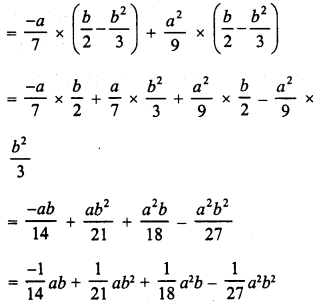
Question 14.

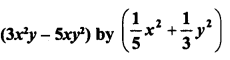
Solution:

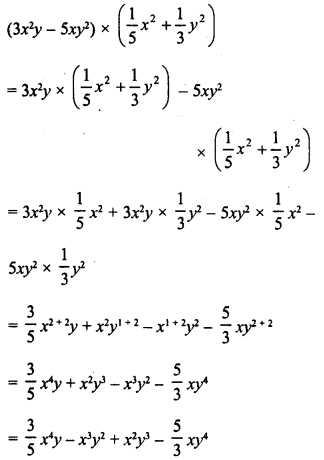
Question 15.
(2x²-1) by (4x³ + 5x²)
Solution:
(2x²-1)x(4x³ + 5x²)
= 2x² x (4x³ + 5x²) – 1 (4x³ + 5x²)
= 2x² x 4x³ + 2x² x 5x² – 4x³ – 5x²
= 8x^{2 + 3} + 10x^{2 + 2}-4x³-5x²
= 8x⁵ + 10x⁴ – 4x³ – 5x²

Question 16.
(2xy + 3y²) (3y² – 2)
Solution:
(2xy + 3y²) (3y² – 2)
= 2xy x (3y²-2) + 3y² x (3y²-2)
= 2xy x Zy²+ 2xy x (-2) + Zy² x Zy² – Zy² x 2
= 6xy^{1 + 2}– 4xy + 9y^{2 + 2}– 6y²
= 6xy³ – 4xy + 9y⁴– 6y²
Find the following products and verify the result for x = -1, y = -2 :

Question 17.
(3x-5y)(x+y)
Solution:
(3x-5y)(x+y)
= 3x x (x + y) – 5y x (x + y)
= 3x x x + 3x x y-5y x x-5y x y
= 3x² + 3xy – 5xy – 5y²
= 3x² – 2xy – 5y²
Verfification:
x = -1,y = -2
L.H.S. = (3x-5y)(x+y)
= [3 (-1) -5 (-2)] [-1 – 2]
= (-3 + 10) (-3) = 7 x (-3) = -21
R.H.S. = 3x² – 2xy – 5y²
= 3 (-1)² – 2 (-1) (-2) -5 (-2)²
=3×1-4-5×4=3-4-20
= 3-24 = -21
∴ L.H.S. = R.H.S.

Question 18.
(x²y-1) (3-2x²y)
Solution:
(x²y-1) (3-2x²y)
= x²y (3 – 2x²y) -1(3-2x²y)
= x²y x 3 – x²y x 2x²y – 1 x 3 + 1 x 2x²y
= 3x²y-2x^{2 + 2}x y^{1 +1}-3 + 2x²y
= 3x²y – 2x⁴y²– 3 + 2x²y
= 3x²y + 2x²y – 2x⁴y² – 3
= 5x²y – 2x⁴y² – 3
Verification : (x = -1, y = -2)
L.H.S. = (x²y – 1) (3 – 2x²y)
= [(-1)² x (-2) -1] [3 – 2 x (-1)2 x (-2)]
= [1 x (-2) -1) [3 – 2 x 1 x (-2)]
= (-2 – 1) (3 + 4) = -3 x 7 = -21
R.H.S. = 5x²y – 2x⁴y² – 3
= 5 (-1)² (-2) -2 (-1)⁴ (-2)² -3
5 x 1 (-2) – 2 (1 x 4) -3
= -10-8-3 = -21
∴ L.H.S. = R.H.S

Question 19.

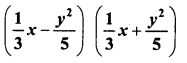
Solution:

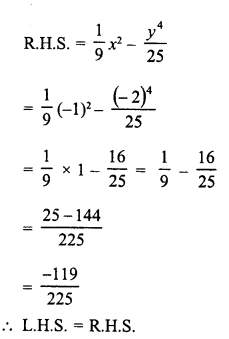
Simplify :

Question 20.
x² (x + 2y) (x – 3y)
Solution:
x² (x + 2y) (x – 3y)
= x² [x (x – 3y) + 2y (x – 3y)]
= x² [x² – 3xy + 2xy – 6y²]
= x² [x² – xy – 6y²)
= x² x x² – x² x xy – x²6y²
= x⁴ – x³y – 6x²y²

Question 21.
(x² – 2y²) (x + 4y)
Solution:
(x² – 2y²) (x + 4y) x²y²
= [x² (x + 4y) -2y² (x + 4y)] x²y²
= (x³ + 4x²y – 2xy² – 8y³) x²y²
= x²y² x x³ + x²y² x 4x²y – 2x²y² x xy² – 8x²y² x y³
= x^{2 +3} y² + 4x^{2 + 2} y^{2 +1} – 2x^{2 +1} y^{2+ 2} – 8x²y²⁺³
= xy + 4⁴xy³ – 2x³y⁴ – 8x²y⁵

Question 22.
a²b² (a + 2b) (3a + b)
Solution:
a²b² (a + 2b) (3a + b)
= a²b² [a (3a + b).+ 2b (3a + b)]
= a²b² [3a² + ab + 6ab + 2b²]
= a²b² [3a² + lab + 2b²]
= a²b² x 3a² + a²b² x 7ab + a²b² x 2b²
= 3a^{2 + 2}b² + 7a²⁺¹ b²⁺¹+ 2a²b^{2 + 2}
= 3a⁴b² + 7a³b³ + 2a²b⁴

Question 23.
x² (x-y) y² (x + 2y)
Solution:
x² (x -y) y² (x + 2y)
= [x² x x – x² x y] [y² x x + y² x 2y]
= (x³ – x²y) (xy² + 2y³)
= x³ (xy² + 2y³) – x²y (xy² + 2y³)
= x³ x xy² + x³ x 2y³ – x²y x xy² – x²y x 2y³
= x^{3 +1} y² + 2x³y³ – x^{2 +1} y^{1+ 2} – 2x²y^{1 + 3}
= x⁴y² + 2x³y³ – x³y³ – 2x²y⁴
= x⁴y² + x³y³ – 2x²y⁴

Question 24.
(x³ – 2x² + 5x-7) (2x-3)
Solution:
(x³ – 2x² + 5x – 7) (2x – 3)
= (2x – 3) (x³ – 2x² + 5x – 7)
= 2x (x³ – 2x² + 5x – 7) -3 (x³ – 2x² + 5x – 7)
= 2x x x³ – 2x x 2x² + 2x x 5x – 2x x 7 -3 x x³ – 3 x (-2x²) – 3 x 5x – 3 x (-7)
= 2x⁴-4x³ + 10x²– 14x-3x³ + 6x²– 15x + 21
= 2x⁴ – 4x³ – 3x³ + 10x² + 6x²– 14x- 15x + 21
= 2x⁴-7x³ + 16x²-29x+ 21

Question 25.
(5x + 3) (x – 1) (3x – 2)
Solution:
(5x + 3) (x – 1) (3x – 2)
= (5x + 3) [x (3x – 2) -1 (3x – 2)]
= (5x + 3) [3x² – 2x – 3x + 2]
= (5x + 3) [3x² – 5x + 2]
= 5x (3x² – 5x + 2) + 3 (3x² – 5x + 2)
= (5x x 3x² – 5x x Sx + 5x x 2)+ [3 x 3x² + 3 x (-5x) + 3×2]
= 15x³ – 25x² + 10x + 9x² – 15x + 6
= 15x³ – 25x² + 9x² + 10x – 15x + 6
= 15x³ – 16x² – 5x + 6

Question 26.
(5-x) (6-5x) (2-x)
Solution:
(5-x) (6-5x) (2-x)
= [5 (6 – 5x) -x (6 – 5x)] (2 – x)
= [30 – 2$x – 6x + 5x²] (2 – x)
= (30 – 3 1x + 5x²) (2-x)
= 2 (30 – 31x + 5x²) – x (30 – 31x + 5x²)
= 60 – 62x + 10x² – 30x + 3 1x² – 5x³
= 60 – 62x – 30x + 10x² + 3 1x² – 5x³
= 60 – 92x + 41x² – 5x³

Question 27.
(2x² + 3x – 5) (3x² – 5x + 4)
Solution:
(2x² + 3x – 5) (3x² – 5x + 4)
= 2x² (3x² – 5x + 4) + 3x (3x² – 5x + 4) -5 (3x² – 5x + 4)
= 2x² x 3x² – 2x² x 5x + 2x² x 4 + 3x x 3x² – 3x x 5x + 3x x 4 – 5 x 3x² – 5 (-5x) -5×4
= 6x⁴ – 10x³ + 8x² + 9x³ – 15x² + 12x – 15x² + 25x-20
= 6x⁴ – 10x³ + 9x³ + 8x² – 15x² – 15x² + 12x + 25x – 20
= 6x⁴ – x³ – 22x² + 37x – 20

Question 28.
(3x – 2) (2x – 3) + (5x – 3) (x + 1)
Solution:
(3x – 2) (2x – 3) + (5x – 3) (x + 1)
= 3x (2x – 3) -2 (2x – 3) + 5x (x + 1) – 3 (x + 1)
= 6x² – 9x – 4x + 6 + 5x² + 5x – 3x – 3
= 6x² + 5x² – 9x – 4x + 5x – 3x + 6 – 3
= 11x²– 11x + 3

Question 29.
(5x – 3) (x + 2) – (2x + 5) (4x – 3)
Solution:
(5x – 3) (x + 2) – (2x + 5) (4x – 3)
= [5x (x + 2) -3 (x + 2)] – [2x (4x – 3) + 5 (4x – 3)]
= [5x² + 1 0x – 3x – 6] – [8x² – 6x + 20x -15]
= (5x² + 7x – 6) – (8x² + 14x – 15)
= 5x² + lx – 6 – 8x² – 14x + 15
= 5x² – 8x² + 7x – 14x – 6 + 15
= -3x² – 7x + 9

Question 30.
(3x + 2y) (4x + 3y) – (2x – y) (7x – 3y)
Solution:
(3x + 2y) (4x + 3y) – (2x – y) (7x – 3y)
= [3x (4x + 3y) + 2y (4x + 3y)]-[2x (7_x-3y)-y(7_x-3y)]
= (12x² + 9xy + 8xy + 6y²) – (14x² – 6xy – 7xy + 3y²)
= (12x² + 17xy + 6y²) – (14x² – 13xy + 3y²)
= 12x² + 17xy + 6y² – 14x² + 13xy – 3y²
= 12x² – 14x² + 17xy + 13xy + 6y² – 3y²
= -2x² + 30xy + 3y²
= -2x² + 3y² + 30xy

Question 31.
(x²-3x + 2) (5x- 2) – (3x² + 4x-5) (2x- 1)
Solution:
(x²-3x + 2) (5x- 2) – (3x² + 4x-5) (2x- 1)
= [5x (x² – 3x + 2) -2 (x² – 3x + 2)] – [2x (3x² + 4x – 5) -1 (3x² + 4x – 5)]
= [5x³ – 15x² + 10x – 2x² + 6x – 4] – [6x³ + 8x² – 10x – 3x² – 4x + 5]
= [5x³ – 15x² – 2x² + 10xc + 6x – 4] – [6x³ + 8x² – 3x² – 10x – 4x + 5]
= (5x³ – 17x² + 16x-4) – (6x³ + 5x² – 14x + 5)
= 5x³ – 17x² + 16x – 4 – 6x³ – 5x² + 14x – 5
= 5x³ – 6x³ – 17x² – 5x² + 16x + 14x – 4 – 5
= -x³ – 22x² + 30x – 9

Question 32.
x³ – 2x² + 3x – 4) (x – 1) – (2x – 3) (x² – x + 1)
Solution:
(x³ – 2x² + 3x – 4) (x – 1) – (2x – 3) (x² – x + 1)
= [x (x³ – 2x² + 3x – 4) – 1 (x³ – 2x² + 3x – 4)] – [2x (x² – x + 1) – 3 (x² – x + 1)]
= [x⁴ – 2x³ + 3x² – 4x – x³ + 2x² – 3x + 4] [2x³ – 2x² + 2x – 3x² + 3x – 3]
= (x⁴ – 2x³ – x³ + 3x² + 2x² – 4x – 3x + 4) (2x³ – 2x² – 3x² + 2x + 3x – 3)
= (x⁴ – 3x³ + 5x² – 7x + 4) – (2x³ – 5x² + 5x – 3)
= x⁴ – 3x³ + 5x² – 7x + 4 – 2x³ + 5x² – 5x + 3
= x⁴ – 3x³ – 2x³ + 5x² + 5x² – 7x – 5x + 4 + 3
= x⁴ – 5x³ + 10x² – 12x + 7

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.