RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.4

RD Sharma Class 8 Solutions Chapter 9 Linear Equations in One Variable Ex 9.4

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.4

Other Exercises

• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.1
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.2
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.3
• RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.4

Question 1.
Four-fifth of a number is more than three-fourth of the number by 4. Find the number.
Solution:
Let the required number = x
Then four-fifth of the number = \(\frac { 4 }{ 5 }\)x
and three- fourth =  \(\frac { 3 }{ 4 }\)x

Question 2.
The difference between the squares of two consecutive numbers is 31. Find the numbers.
Solution:
Let first number = x
There second number = x + 1
∴ According to the condition :
(x + 1)² – (x)² = 31
⇒ x² + 2x + 1 – x² = 31
⇒ 2x = 31 – 1 = 30 30
⇒ x =  \(\frac { 30 }{ 2 }\) = 15
∴  First number = 15
and second number = 15 + 1 = 16
Hence numbers are 15, 16
Check : (16)² – (15)² = 256 – 225 = 31
Which is given
∴  Our answer is correct.

Question 3.
Find a number whose double is 45 greater than its half.
Solution:
Let the required number = x
Double of it = 2x
and half of it =  \(\frac { x }{ 2 }\)
According to the condition :

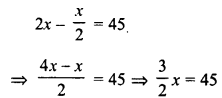
Question 4.
Find a number such that when 5 is subtracted from 5 times the number, the result is 4 more than twice the number.
Solution:
Let the required number = x 5
times of it = 5x
twice of it = 2x
According to the condition :
5x – 5 = 2x + 4
⇒ 5x – 2x = 4 + 5
⇒ 3x = 9
⇒ x =\(\frac { 9 }{ 3 }\)   = 3
Required number = 3
Check :3 x 5-5 = 2×3+4
⇒  15-5 = 6 + 4
⇒ 10= 10
Which is true. Therefore our answer is correct.

Question 5.
A number whose fifth part increased by 5 is equal to its fourth part diminished by 5. Find the number.
Solution:
Let the number = x
Then fifth part increased by 5 = \(\frac { x }{ 5 }\) + 5
Fourth part diminished by 5 = \(\frac { x }{ 4 }\)  – 5
According to the condition :

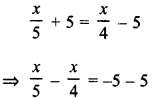
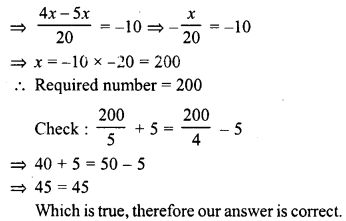
Question 6.
A number consists of two digits whose sum is 9. If 27 is subtracted from the number, its digits are reversed. Find the number.
Solution:
Sum of two digits = 9
Let units digit = x
Then tens digit = 9 – x
and number = 10 (9 – x) + x
= 90 – 10x + x = 90 -9x
On reversing the digits,
Units digit = 9 -x tens digit = x
and number = 10 (x) + 9 – x
= 10x + 9- x = 9x + 9
According to the condition :
90 – 9x – 27 = 9x + 9
⇒ 9x + 9x = 90 – 27-9
⇒ 18x = 90- 36 = 54
⇒ x =\(\frac { 54 }{ 18 }\) = 3
Number = 90 – 9x = 90 – 9 x 3 = 90 – 27 = 63
Check : 63 – 27 = 36 (Whose digits are reversed)
Which is true. Therefore our answer is correct.

Question 7.
Divide 184 into two parts such that one- third of one part may exceed one seventh of another part by 8.
Solution:
Sum of two parts = 184
Let first part = x
Then second part = 184 – x
According to the condition :

Question 8.
The numerator of a fraction is 6 less than the denominator. If 3 is added to the numerator, the fraction is equal to \(\frac { 2 }{ 3 }\) . What is the original fraction equal to ?
Solution:
Let denominator of the original fraction = x
Then numerator = x – 6
and fraction = \(\frac { x-6 }{ x }\)
According to the condition :

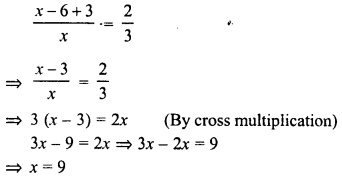
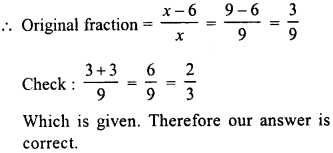
Question 9.
A sum of Rs. 800 is in the form of denominations of Rs. 10 and Rs. 20. If the total number of notes be 50, find the number of notes of each type.
Solution:
Total amount = Rs. 800
Total number of notes = 50
Let number of notes of Rs. 10 = x
Then number of notes of Rs. 20 = 50 – x
According to the condition, x x 10 + (50-x) x 20 = 800
⇒  10x + 1000 – 20x = 800
⇒  -10x = 800- 1000 = -200
⇒ x =   \(\frac { -200 }{ -10 }\) = 20
∴ Number of 10-rupees notes = 20
and number of 20-rupees notes = 50-20 = 30
Check : 20 x 10 + 30 x 20
= 200 + 600 = 800
Which is true. Therefore our answer is correct.

Question 10.
Seeta Devi has Rs. 9 in fifty-paise and twenty five-paise coins. She has twice as many twenty-five paise coins as she has fifty-paise coins. How many coins of each kind does she have ?
Solution:
Total amount = Rs. 9
Let fifty paise coins = x
Then twenty-five paise coins = 2x
According to the condition :

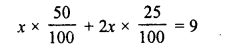
Question 11.
Sunita is twice as old as Ashima. If six years is subtracted from Ashima’s age and four years added to Sunita’s age, then Sunita will be four times Ashima’s age. How old were they two years ago ?
Solution:
Let age of Ashima = x
Then age of Sunita = 2x
According to the condition :
4 (x – 6) = 2x + 4
⇒  4x-24 = 2x + 4
⇒ 4x-2x = 4 + 24
⇒  2x = 28
⇒ x = \(\frac { 28 }{ 2 }\) = 14
∴  Sunita’s present age = 2x = 2 x 14 = 28 years
and Ashima’s age = 14 years
Two years ago,
Age of Sunita = 28 – 2 = 26 years
and age of Ashima =14-2 = 12 years

Question 12.
The ages of Sonu and Monu are in the ratio 7 : 5. Ten years hence, the ratio of their ages will be 9 : 7. Find their present ages.
Solution:
Ratio in the present ages of Sonu and Monu = 7:5
Let age of Sonu = 7x years
and age of Monu = 5x years
10 years hence,
the age of Sonu = 7x + 10 years
and age of Monu = 5a + 10 years
According to the condition :

Question 13.
Five years ago a man was seven times as old as his son. Five years hence, the father will be three times as old as his son. Find their present ages.
Solution:
5 years ago,
Let age of son = x years
Then, age of father = 7a years
Present age of son = x + 5 years
and age of father = 7x + 5 years
5 years hence,
age of son = x + 5 + 5= x+10
and age of father = 7x + 5 + 5 = 7x + 10
According to the condition :
7x + 10 = 3 (x + 10)
⇒  7x + 10 = 3x + 30
⇒  7x -3x= 30 – 10 = 20

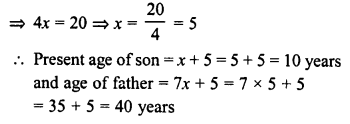
Question 14.
I am currently 5 times as old as my son. In 6 years time I will be three times as old as he will be then. What are our ages now ?
Solution:
Let present age of my son = x years
Then my age = 5x years
After 6 years,
my age will be = 5x + 6
and my son’s age = x + 6
According to the condition
5x + 6 = 3 (x + 6)
⇒ 5x+ 6 = 3x+ 18
⇒ 5x – 3x = 18 – 6 ⇒ 2x = 12
⇒ x = 6
∴ Present my age = 5x = 5 x 6 = 30 years
and my son’s age = 6 years

Question 15.
I have Rs. 1000 in ten and five rupees notes. If the number of ten rupees notes that I have is ten more than the number of five rupees notes, how many notes do I have in each denomination ?
Solution:
Total amount = Rs. 1000
Let the number of five rupee notes = x
∴ Ten rupees notes = x + 10
According to the condition,
(x + 10) x 10 + 5 x x x = 1000
⇒ 10a + 100 + 5a = 1000
⇒  15a = 1000- 100 = 900
⇒ x = \(\frac { 900 }{ 15 }\) = 60
∴  Number of five rupees notes = 60
and number of ten rupees notes = 60 + 10 = 70

Question 16.
At a party, colas, squash anjd fruit juice were offered to guests. A fourth of the guests drank colas, a third drank squash, two fifths drank juice and just three did not drink any thing. How many guests were in all ?
Solution:
Let total number of guests = x
Guests who drank colas = \(\frac { x }{ 4 }\)
Guests who drank squash = \(\frac { x }{ 3 }\)
Guests who drank juice = \(\frac { 2 }{ 5 }\) x
Guest who drank none of these = 3
According to the condition :

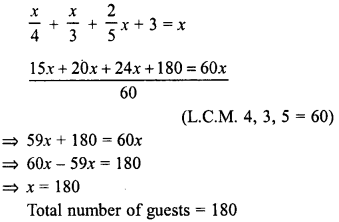
Question 17.
There are 180 multiple choice questions in a test. If a candidate gets 4 marks for every correct answer and for every unattempted or wrongly answered question one mark is deducted from the total score of correct answers. If a candidate scored 450 marks in the test, how many questions did he answer correctly ?
Solution:
Number of total questions = 180
Let the candidate answers questions correctly = x
∴ Uncorrect or unattended questions =180 -x
total score he got = 450
According to the condition
x x 4-(180-x) x 1 =450
⇒ 4x – 180 + x = 450
⇒ 5x = 450+ 180 = 630
⇒ x =\(\frac { 630 }{ 5 }\) = 126
Number of question which answered correctly = 126

Question 18.
A labourer is engaged for 20 days on the condition that he will receive Rs. 60 for each day, he works and he will be fined Rs. 5 for each day, he is absent, If he receives Rs. 745 in all, for how many days he remained absent ?
Solution:
Total number of days = 20
Let number of days he worked = x
Then number of days he remained absent = 20 – x
According to the condition :
x x 60 – (20 – x) x 5 = 745
⇒  60x- 100 + 5x = 745
⇒  65x = 745 + 100 = 845
⇒  x = \(\frac { 845 }{ 65 }\) = 13
∴ Number of days he worked =13 days
and number of days he remained absent = 20 – 13 = 7 days.

Question 19.
Ravish has three boxes whose total weight is 60 \(\frac { 1 }{ 2 }\) kg. Box B weighs 3\(\frac { 1 }{ 2 }\) kg more it than A and box C weighs 5\(\frac { 1 }{ 3 }\) kg more than box B. Find the weight of box A.
Solution:
Total weight of three boxes = 60\(\frac { 1 }{ 2 }\) kg.
Let weight of box A = x kg.

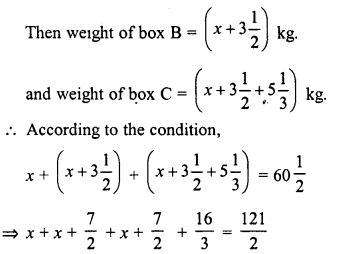
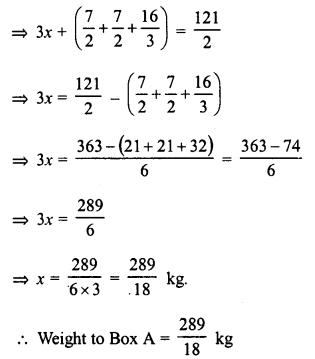
Question 20.
The numerator of a rational number is 3 less than the denominator. If the denominator is increased by 5 and the numerator by 2, we get the rational number \(\frac { 1 }{ 2 }\). Find the rational number.
Solution:
Let denominator of the given rational number = x
Then numerator = x – 3
∴ Rational number =\(\frac { x – 3 }{ x }\)
According to the condition :

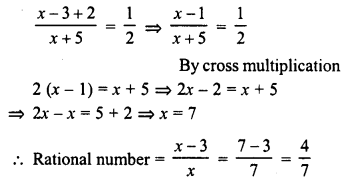
Question 21.
In a rational number, twice the numerator is 2 more than the denominator. If 3 is added to each, the numerator and the denominator, the new fraction is \(\frac { 2 }{ 3 }\) . Find the original number.
Solution:

Question 22.
The distance between two stations is 340 km. Two trains start simultaneously from these stations on parallel tracks to cross each other. The speed of one of them is greater than that of the other by 5 km/ hr. If the distance between the two trains after 2 hours of their start is 30 km, find the speed of each train.
Solution:
Distance between two stations = 340 km.
Let the speed of the first train = x km/hr.
Then speed of second train = (x + 5) km/h.
Time = 2 hours
Distance travelled by the first train in 2 hours = 2x km
and distance travelled by the second train = 2 (x + 5) km
According to the condition,

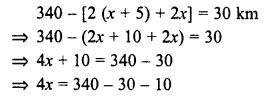
Question 23.
A steamer goes downstream from one point to another in 9 hours. It covers the same distance upstream in 10 hours. If the speed of the stream be 1 km/hr, find the speed of the steamer in still water and the distance between the ports.
Solution:
Time taken by a steamer downstream = 9 hours
and upstream = 10 hours Speed of steamer = 1 km/hr.
Let speed of the steamer = x km/h.
According to the condition :
9 (x + 1) = 10 (x – 1)
9x + 9 = 10x – 10 ⇒ 10x – 9x = 9 + 10
⇒ x = 19
∴  Speed of steamer in still water =19 km/h
and distance between two ports = 9 (a + 1) = 9 (19 + 1) = 9 x 20 = 180 km.

Question 24.
Bhagwanti inherited Rs. 12000.00 She invested part of it as 10% and the rest at 12%. Her annual income from these investments is Rs. 1280.00. How much did she invest at each rate ?
Solution:
Total investment = Rs. 12000.00
Rate of interest for first part = 10%
and for second part = 12%
Annual income = Rs. 1280.00
Let the investment for the first part = Rs. x
and second part = Rs. (12000 – x)
According to the condition :

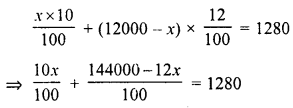
Question 25.
Total investment = Rs. 12000.00 Rate of interest for first part = 10% and for second part = 12% Annual income = Rs. 1280.00 Let the investment for the first part = Rs. a and second part = Rs. (12000 – a) According to the condition :
Solution:
Let breadth of the rectangle = x cm
Then length = (x + 9) cm
∴ Area = length x breadth = x (x + 9) cm²
By increasing each length and breadth by 3 cm
The new length of the rectangle = x + 9 + 3
= (x + 12) cm
and breadth = (x + 3) cm
∴  Area = (x + 12) (x + 3)
According to the condition :
(x + 12) (x + 3) – a (x + 9) = 84
x² + 3x + 12x + 36 – x² – 9x = 84
⇒ 6a = 84 – 36 = 48 ⇒ x  = \(\frac { 48 }{ 6 }\) =8
∴  Length of the rectangle = a + 9 = 8 + 9 = 17 cm
and breadth =x = 8 cm.

Question 26.
The sum of the ages of Anup and his father is 100. When Anup is as old as his father now, he will be five times as old as his son Anuj is now. Anuj will be eight years older than Anup is now, when Anup is as old as his father. What are their ages now ?
Solution:
Sum of ages of Anup and his father =100 years
Let present age of Anup = x years
∴  Age of his father = (100 – x) years
∴  Age of Anuj = \(\frac { 100 – x  }{ 5 }\) years
and also Anuj’s age = (x + 8) years ….I
Anup becomes as old as his father is now
after (100 – 2x) years
∴ After (100 – 2x) years

Question 27.
A lady went shopping and spent half of what she had on buying hankies and gave a rupee to a begger waiting outside the shop. She spent half of what was left on a lunch and followed that up with a two rupee tip. She spent half of the remaining amount on a book and three rupees on bus fare. When she reached home, she found that she had exactly one rupee left. How much money did she start with ?
Solution:
Let the amount, a lady has in the beginning = Rs. x

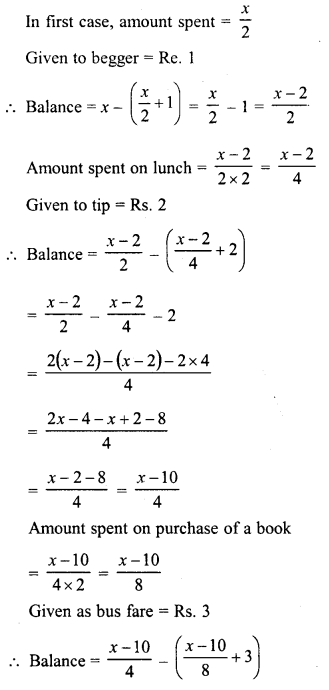
Hope given RD Sharma Class 8 Solutions Linear Equations in One Variable Ex 9.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.