By going through these CBSE Class 12 Maths Notes Chapter 1 Relations and Functions, students can recall all the concepts quickly.
Relations and Functions Notes Class 12 Maths Chapter 1
RELATION
1. Types of Relations
→ Empty Relation: A relation in a set A is known as empty relation, if no element of A is related to any element of A, i.e., R = Φ ⊆ A × A. e.g.
Let the set A = {1, 2,3,4,5) and R is given by
R= {(a,b): a – b = 20}
There is no pair (a, b) that satisfies the condition
a – b = 20.
⇒ The relation R is the empty relation.
→ Universal Relation: A relation R in a set A is called a universal relation, if each element of A is related to every element of A, i.e.,
R = A × A. e.g.
Let the set A = {1, 2,3, 4,5} and R is given by R = {(a, b): ab > 0}
Here, R = {(a, b): ab > 0} is the whole set A × A as all pairs (a, b) in A × A satisfy ab > 0.
Thus, this is the universal relation.
→ A relation R in a set A is called
(a) reflexive: if (a, a) ∈ R for every a ∈ A.
(b) symmetric: ii (a, b) ∈ R implies that (b, a) ∈ R for all a, b ∈ A.
(c) transitive: if (a, b) ∈ R and (b, c) e R implies that (a, c) ∈ R for all a,b,c ∈ A.
→ Equivalence Relation: A relation R in A is an equivalence relation if R is reflexive, symmetric, and transitive. For example:
(1) Let T be the set of all triangles in a plane with R a relation in T given by
R = ((T1, T2): T1 is similar to T2)
(a) R is reflexive since every triangle is similar to itself.
(b) (T1, T2) ∈ R ⇒ T1 is similar to T2.
(T2, T3) ∈ R ⇒ T2 is similar to T1
Therefore, R is symmetric.
(c) (T1, T2) and (T2, T3) lies in R
⇒ T1 is similar to T2 and T2 is similar to T3, which means T1 is similar to T3,
i.e., (T1, T3) lies in R.
∴ R is transitive.
Now R is reflexive, symmetric, and transitive, therefore R is an equivalence relation.
(2) Consider the set A = {1,2,3,4} and the relation R = {(1,1), (2, 2), (3,3), (4, 4), (1, 2), (2, 3), (3, 4)}.
(a) Now (1,1), (2, 2), (3, 3), (4, 4) lie in R. Relation R is reflexive.
(b) (1, 2) lies in R but (2,1) does not lie in it.
∴ It is not symmetric.
(c) (1,2), (2, 3) lie in R but (1, 3) does not lie in it. Therefore, R is not transitive.
Here, R is reflexive but neither symmetric nor transitive. Therefore, R is not an equivalence relation.
2. Equivalence Class [a] containing a
For an arbitrary equivalence relation R in an arbitrary set X, R divides X into mutually disjoint subsets Ai, which are known as partitions or sub-divisions of X satisfying:
(a) All elements of Ai are related to each other for all i.
(b) No element of Ai is related to any element of Aj, i ≠ j.
(c) ∪ Aj = X and Ai ∩ A. = Φ, i ≠ j.
The subsets Af are said to be equivalence classes.
Example: Let R be the relation defined in the set A = {p, q, s, t, e, o, u} by
R = {(a, b): both a and b are either consonants or vowels,
Here, R is an equivalence relation.
(a) Any element ∈ A is either consonant or vowel,
i.e., (a, a) ∈ R ⇒ R is reflexive.
(b) If (a, b) ∈ R ⇒ a and b both are either consonants or vowels ⇒ (b, a) e R.
∴ R is symmetric.
(c) If (a, b) ∈ R and (b, c) ∈ R, then a, b; b, c both pairs are either consonants or vowels.
i.e., a, b, c all are either consonants or vowels.
⇒ (a, c) ∈ R.
∴ R is transitive.
Thus, R is an equivalence relation.
Further, all the elements of (p, q, s, t) are related to each other as all the elements of this subset are consonants.
Similarly, all the elements of {e, i, o, u } are related to each other as all of them are vowels. But no element of {p, q, s, t} can be related to any element of {e, i, o, u}, since the elements of {p, q, s, t} are all consonants and the elements of {e, i, o, u} are all vowels. {p, q, s, t} is an equivalence class.denoted by an element as {p}. Similarly, {e, i, o, u} is an equivalence class denoted by an element [e).
FUNCTIONS
1. Types of Functions
→ One-one (or Injective): A function f: X → Y is said to be one-one (or injective), if the images of the distinct elements of X under/are distinct, i.e., for every x1, x2 ∈ X, if f(x1) = f(x2) implies that x1 = x2.
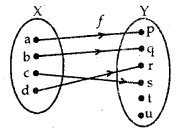
Each element of X has a distinct image in Y. Such a function or a mapping is one-one.
→ Onto (or surjective): A function f: X →Y is called onto, if every element of Y is the image of some element of X under f, i.e., for all y ∈ Y, there exists an element x in X such that f(x) = y.
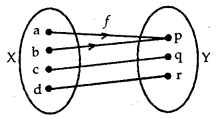
Corresponding to each element of Y, there is a pre-image in X. Such a mapping is onto.
→ One-one and Onto (Bijective): A function f: X to Y is known as one-one and onto (or bijective), if f is both one-one and onto.
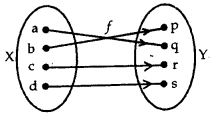
Here,f is both one-one and onto. Therefore,f is said to be one-one onto function or bijective function.
2. Composition of Functions
Let f: A → B and g: B → C be the two functions. The composition of f and g is defined as. gof: A → C, such that
gof(x) = g{f(x)}, for all x ∈ A.
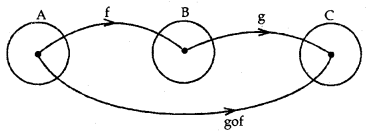
A function f: X → Y is said to be invertible if there exists a function g: Y → X such that gof = Ix and fog = Iy. The function g is called the inverse of f. It is denoted by f-1.
Inverse or composite function: If f: X →Y and g: Y → Z be the two invertible functions, then gof is also invertible such that (gof)-1 = f-1og-1
BINARY OPERATION
→ Binary Operation: A binary operation on a set A is a function X: A × A → A, defined by × (a,b) = a × b, e.g., ×: R × R → R is given by (a, b) → a + b. Here +, — and x are the functions but + : R × R →, R, written as (a, b) → \(\frac{a}{b}\) is not a function. It is not a binary operation, since it is not defined for b = O.
→ Commutative Binary Operation: A binary operation × on the set A is commutative,if for every a,b ∈ A, a × b = b × a.
→ Associative Binary Operation: A binary operation × on the set A is associative, if (a × b) × c = a × (b × c).
It may be noted that associative property, a × b × c × d, … is not defined unless brackets are used.
→ An Identity Element e for Binary Operation: Let ×: A × A → A be a binary operation. There exists an element e ∈ A such that a × e = a = e × a, for all a ∈ A.
The element e is known as the identity element. It should be noted that 0 is the identity element for addition but not for natural numbers N, since 0 ∉ N.
→ The inverse of an element a: Let ×: A × A → A be a binary operation with identity element e in A. An element a ∈ A is invertible w.r.t. binary operation ×, if there exists an element b in A such that a × b = e = b × a. The element b is said to be the inverse of a. It is denoted by a-1, e.g.,
– a is the inverse of a for the operation of addition +.
\(\frac{1}{a}\) (a ≠ 0) is the inverse of a for multiplication.
1. RELATIONS
(i) Relation. A relation R from a set A to a set B is a subset of A x B.
(ii) Classification of Relations : a
(a) Reflexive Relation. A relation R in a set E is said to be reflexive if xRx ∀ x ∈ E.
(b) Symmetric Relation. A relation R in a set E is said to be symmetric if:
xRy = yRx ∀ x, y ∈ E.
(c) Transitive Relation. A relation R in a set E is said to be transitive if:
vRy and yRz ⇒ xRz ∀ x, y, z ∈ E.
(d) Equivalence Relation. A relation R in a set E is said to be an equivalence relation if it is :
- reflexive
- symmetric and
- transitive.
2. FUNCTIONS
(i) Let X and Y be two non-empty sets. Then ‘f’ is a rule, which associates to each element x in X . a unique element y in Y.
(a) The unique element y of Y is called the value of f at x.
(b) The element x of X is called pre-image of y.
(c) The set X is called the domain of f
(d) The set of images of elements of X under f is called the range of f.
(ii) (a) Df = {x : x ∈ R, f(x) ∈ R}
(b) Rf = {f(x):x ∈ Df}
(c) f is one-one iff x1 = x2
⇒ f(x1) = f(x2) for x1, x2 ∈ Df
or iff x1 ≠ x2
⇒ f(x1) ≠ f(x2) for x1, x2 ∈ Df
(d) f is invertible iff f is one-one onto and Df-1 = Rf, Rf-1= DRf.
3. ALGEBRA OF FUNCTIONS
Let f and g be two functions. Then
(i) (f+g) (x) =f(x) + g(x); Df+g = Df ∩ Dg
(ii) (f- g) (x) = f(x) – g(x); Df-g = Df ∩ Dg
(iii) (fg) (x) =f(x) g(x); Dfg = Df ∩ Dg
(iv) \(\left(\frac{f}{g}\right) x=\frac{f(x)}{g(x)}\); Df/g = Df ∩ Dg – {x:x∈Dg, g(x) = 0}