RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15.
Question 1.
Solution:
(i) Four
(ii) Four
(iii) 4, collinear
(iv) two
(v) opposite
(vi) 360°
Question 2.
Solution:
(i) There are four pairs of adjacent sides which are (AB, BC), (BC, CD), (CD, DA) and (DA, AB)
(ii) There are two pairs of opposite sides which are (AB, CD) and (BC, AD)
(iii) There are four pairs of adjacent angles which are (∠ A, ∠ B), (∠ B, ∠ C), (∠ C, ∠ D) and (∠ D, ∠ A)
(iv) There are two pairs of opposite angles which are (∠A, ∠C) and (∠B, ∠D)
(v) There are two diagonals which are AC and BD.
Question 3.
Solution:
Given : ABCD is a quadrilateral
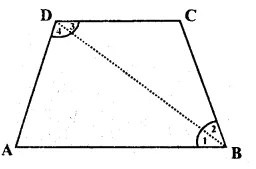
To prove : ∠A + ∠B + ∠C + ∠D = 360°
Construction : Join BD
Proof : In ∆ ABD,
∠ A + ∠1 + ∠ 4 = 180° (sum of angles of a triangle)
Similarly ∠2 + ∠C + ∠ 3 = 180° Adding we get,
∠ A + ∠1 + ∠4 + ∠2 + ∠C + ∠ 3
= 180° + 180°
=> ∠A + ∠1 + ∠2 + ∠C + ∠3 + ∠4 = 360°
=> ∠A + ∠B + ∠C + ∠D = 360° Hence proved.
Question 4.
Solution:
We know that
Sum of 4 angles of a quadrilateral = 360°
But sum of 3 angles = 76° + 54° + 108°
= 238°
4th angle = 360 – 238°
= 122°
Hence, measure of fourth angle = 122° Ans
Question 5.
Solution:
Ratio of four angles of a quadrilateral = 3 : 5 : 7 : 9
Let these angles be 3x, 5x, 7x and 9x
then 3x + 5x + 7x + 9x = 360° (sum of angles)
=> 24x = 360°
First angle = 3x = 3 x 15° = 45°
Second angle = 5x = 5 x 15° = 75°
Third angle = 7x = 7 x 15° = 105°
Fourth angle = 9x = 9 x 15° = 135° Ans.
Question 6.
Solution:
Three acute angles of a quadrilateral are 75° each
Sum of three angles = 3 x 75° = 225°
But sum of 4 angles = 360°
Fourth angle = 360° – 225°
= 135° Ans.
Question 7.
Solution:
Sum of 4 angles of a quadrilateral 360°
One angles = 120°
Sum of other three angles = 360° – 120° = 240°
But each of these 3 angles are equal
Each of equal angles = \(\frac { 240^{ o } }{ 3 } \)
= 80°
Question 8.
Solution:
Sum of 4 angles of a quadrilateral = 360°
Sum of two angles = 85° + 75° = 160°
Sum of other two angles = 360° – 160° = 200°
But each of these two angles are equal
Measure of each equal angle = \(\frac { 200^{ o } }{ 2 } \)
= 100° Ans.
Question 9.
Solution:
In quadrilateral ABCD
∠C = 100°, ∠D = 60°
and ∠A + ∠B + ∠C + ∠D = 360°
(sum of angles of a quadrilateral)
∴ ∠ A + ∠ B = 360° – (100° + 60°)
= 360° – 160° = 200°
But AP and BP are the bisectors of ∠ A and ∠ B
∴ \(\\ \frac { 1 }{ 2 } \) – (∠ A + ∠B) = 200° x \(\\ \frac { 1 }{ 2 } \) = 100°
i.e. ∠ 1 + ∠2 = 100°
But in ∆ APB,
∠1 + ∠2 + ∠P = 180°
=> 100° + ∠P = 180°
=> ∠P = 180° – 100° = 80°
or ∠APB = 80° Ans.
Hope given RS Aggarwal Class 8 Solutions Chapter 15 Quadrilaterals Ex 15 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for yo