RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14G

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14G.

Other Exercises

Question 1.
Solution:
Arranging in ascending order, we get:
2,2,3,5,7,9,9,10,11
Here, number of terms is 9 which is odd.
∴ Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 9+1 }{ 2 } \) th term = 5th term = 7 Ans.
(ii) Arranging in ascending order, we get: 6, 8, 9, 15, 16, 18, 21, 22, 25
Here, number of terms is 9 which is odd.
∴ Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 9+1 }{ 2 } \) th term = 5th term = 16 Ans.
(iii) Arranging in ascending order, we get: 6, 8, 9, 13, 15, 16, 18, 20, 21, 22, 25
Here, number of terms is 11 which is odd.
∴ Median = \(\frac { 11+1 }{ 2 } \) th term = \(\frac { 12 }{ 2 } \) th term = 6th term = 16 Ans.
(iv) Arranging in ascending order, we get:
0, 1, 2, 2, 3, 4, 4, 5, 5, 7, 8, 9, 10
Here, number of terms is 13, which is odd.
Median = \(\frac { 13+1 }{ 2 } \) th term = \(\frac { 14 }{ 2 } \) th term = 7th term = 4 Ans.

Question 2.
Solution:
Arranging in ascending order, we get 9, 10, 17, 19, 21, 22, 32, 35
Here, number of terms is 8 which is even
∴Median = \(\frac { 1 }{ 2 } \left[ \frac { 8 }{ 2 } th\quad term+\left( \frac { 8 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) [4th term + 5th term] = \(\frac { 1 }{ 2 } \) (19 + 21) = \(\frac { 1 }{ 2 } \) x 40 = 20
(ii) Arranging in ascending order, we get:
29, 35, 51, 55, 60, 63, 72, 82, 85, 91
Here number of terms is 10 which is even
∴Median = \(\frac { 1 }{ 2 } \left[ \frac { 10 }{ 2 } th\quad term+\left( \frac { 10 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) (60 + 63) = \(\frac { 1 }{ 2 } \) x 123 = 61.5 Ans.
(iii) Arranging in ascending order we get
3, 4, 9, 10, 12, 15, 17, 27, 47, 48, 75, 81
Here number of terms is 12 which is even.
∴Median = \(\frac { 1 }{ 2 } \left[ \frac { 12 }{ 2 } th\quad term+\left( \frac { 12 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) (6th term + 7th term) = \(\frac { 1 }{ 2 } \) (15 + 17)= \(\frac { 1 }{ 2 } \) x 32
= 16 Ans.

Question 3.
Solution:
Arranging the given data in ascending order, we get :
17, 17, 19, 19, 20, 21, 22, 23, 24, 25, 26, 29, 31, 35, 40
∴ Median = \(\frac { 15+1 }{ 2 } \) th term = \(\frac { 16 }{ 2 } \) th term = 8th term = 23
∴ Median score = 23 Ans.

Question 4.
Solution:
Arranging in ascending order, we get:
143.7, 144.2, 145, 146.5, 147.3, 148.5, 149.6, 150, 152.1
Here, number of terms is 9 which is odd.
Median = \(\frac { 9+1 }{ 2 } \) th term = \(\frac { 10 }{ 2 } \) th term = 5th term = 147.3 cm
Hence, median height = 147.3 cm Ans.

Question 5.
Solution:
Arranging in ascending order, we get:
9.8, 10.6, 12.7, 13.4, 14.3, 15, 16.5, 17.2
Here number of terms is 8 which is even
∴Median = \(\frac { 1 }{ 2 } \left[ \frac { 8 }{ 2 } th\quad term+\left( \frac { 8 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \)[4th term + 5th term]
= \(\frac { 1 }{ 2 } \) (13.4 + 14.3) = \(\frac { 1 }{ 2 } \) (27.7) = 13.85
∴ Median weight = 13.85 kg. Ans.

Question 6.
Solution:
Arranging in ascending order, we get:
32, 34, 36, 37, 40, 44, 47, 50, 53, 54
Here, number of terms is 10 which is even.
∴Median = \(\frac { 1 }{ 2 } \left[ \frac { 10 }{ 2 } th\quad term+\left( \frac { 10 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) [5th term + 6th term ] = \(\frac { 1 }{ 2 } \) (40 + 44) = \(\frac { 1 }{ 2 } \) x 84 = 42 .
∴ Median age = 42 years.

Question 7.
Solution:
The given ten observations are 10, 13, 15, 18, x + 1, x + 3, 30, 32, 35, 41
These are even
∴Median = \(\frac { 1 }{ 2 } \left[ \frac { 10 }{ 2 } th\quad term+\left( \frac { 10 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) [5th term + 6th term ] = \(\frac { 1 }{ 2 } \)(x + 1 + x + 3) = \(\frac { 1 }{ 2 } \)(2x + 4)
= x + 2
But median is given = 24
∴ x + 2 = 24 => x = 24 – 2 = 22
Hence x = 22.

Question 8.
Solution:
Preparing the cumulative frequency table, we have:
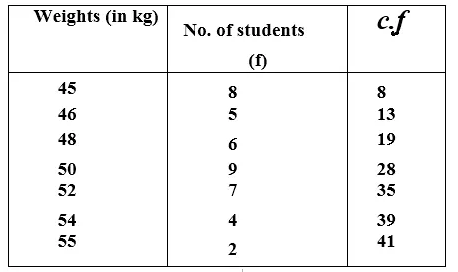
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14G Q8.1
Here, number of terms (n) = 41, which is odd,
Median = \(\frac { 41+1 }{ 2 } \) th term = \(\frac { 42 }{ 2 } \) th term = 21st term = 50 (∵ 20th to 28th term = 50)
Hence median weight = 50 kg Ans.

Question 9.
Solution:
Arranging first in ascending order, we get:
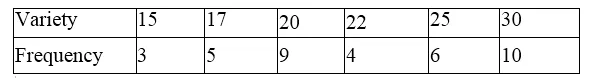
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14G Q9.1
Now preparing its cumulative frequency table

Here, number of terms is 37 which is odd.
Median = \(\frac { 37+1 }{ 2 } \) th term = \(\frac { 38 }{ 2 } \) th term = 19 th term = 22 (∵18th to 21st = 22)
Hence median – 22 Ans.

Question 10.
Solution:
first arranging in ascending order we get
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14G Q10.1
Now preparing its cumulative frequency table,we find:

Here, number of terms is 43, which if odd.
Median = \(\frac { 43+1 }{ 2 } \) th term = \(\frac { 44 }{ 2 } \) th term = 22nd term = 25 25 (∵ 11th to 26th = 25)

Question 11.
Solution:
Arranging in ascending order,we get
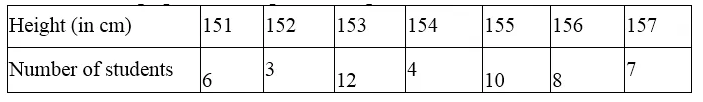
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14G Q11.1
Now preparing its cumulative frequency table, we find :

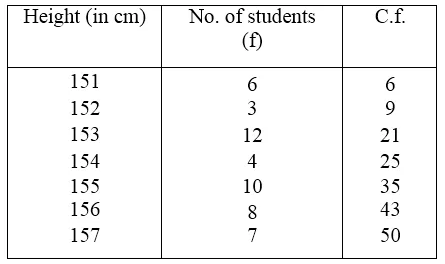
Here, number of terms = 50 which is even
∴Median = \(\frac { 1 }{ 2 } \left[ \frac { 50 }{ 2 } th\quad term+\left( \frac { 50 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) (154 + 155) = \(\frac { 1 }{ 2 } \) (309) = 154.5 (∵ 22nd to 25th = 154, 26th to 34th= 155)

Question 12.
Solution:
Arranging in ascending order, we get:
RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14G Q12.1
Now, preparing its cumulative frequency table.

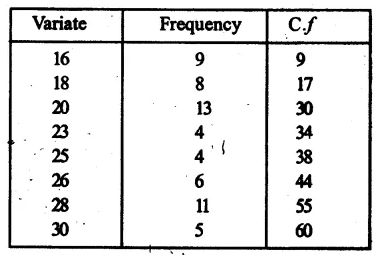
Here, number of terms is 60 which is even
∴Median = \(\frac { 1 }{ 2 } \left[ \frac { 60 }{ 2 } th\quad term+\left( \frac { 60 }{ 2 } +1 \right) th\quad term \right] \)
= \(\frac { 1 }{ 2 } \) (30th term + 31st term)
= \(\frac { 1 }{ 2 } \) (20 + 23) = \(\frac { 1 }{ 2 } \) x 43 = 21.5 (∵ 18th to 30th term = 20, 31st term to 34th = 23)
Hence median = 21.5 Ans.

Hope given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14G are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.