Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking (Recurring Deposit Accounts) Ex 2A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2A.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2B
Question 1.
Manish opens a Recurring Deposit Account with the Bank of Rajasthan and deposits ₹ 600 per month for 20 months. Calculate the maturity value of this account, if the bank pays interest at the rate of 10% per annum.
Solution:
Recurring Deposit per month = ₹ 600
Period (n) = 20 months
Rate of interest (r) = 10% p.a.
Total principal for 1 month
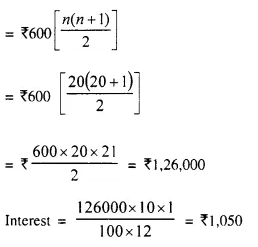
Maturity value = ₹ 600 x 20 + ₹ 1,050 = ₹ 12,000 + ₹ 1,050 = ₹ 13,050
Question 2.
Mrs. Mathew opened a Recurring Deposit Account in a certain bank and deposited ₹ 640 per month for 4\(\frac { 1 }{ 2 }\) years. Find the maturity value of this account, if the bank pays interest at the rate of 12% per year.
Solution:
Recurring deposit per month = ₹ 640
Period (n) = 4\(\frac { 1 }{ 2 }\) years = 54 months
Rate of interest (r) = 12%
Total principal for 1 month

Maturity value = ₹ 640 x 54 + ₹ 9,504 = ₹ 34,560 + ₹ 9,504 = ₹ 44,064
Question 3.
Each of A and B opened a recurring deposit accounts in a bank. If A deposited ₹ 1,200 per month for 3 years and B deposited ₹ 1,500 per month for 2\(\frac { 1 }{ 2 }\) years; find, on maturity, who will it get more amount and by how much ? The rate of interest paid by the bank is 10% per annum.
Solution:
A’s deposit per month (P) = ₹ 1200
Period = 3 years = 36 months
Total principal for one month

![]()
and maturity value = ₹ 1500 x 30 + Interest
= ₹ 45000 + 5812.50
= ₹ 50812.50
It is clear that B’s maturity value is greater Difference = ₹ 50812.50 – ₹ 49860 = ₹ 952.50
Question 4.
Ashish deposits a certain sum of money every month in a Recurring Deposit Account for a period of 12 months. If the bank pays interest at the rate of 11% p.a. and Ashish gets ₹ 12,715 as the maturity value of this account, what sum of money did he pay every month ?
Solution:
Let Recurring deposit per month = ₹ x
Period (n) = 12 months
Rate of interest (r) = 11%
Maturity value = ₹ 12,715 ………. (i)
Total principal for one month

Recurring deposit per month ₹ 1000 p.m.
Question 5.
A man has a Recurring Deposit Account in a bank for 3\(\frac { 1 }{ 2 }\) years. If the rate of interest is 12% per annum and the man gets ₹ 10206 on maturity, find the value of monthly installments.
Solution:
Let Recurring deposit per month = ₹ x
Period (n) = 3\(\frac { 1 }{ 2 }\) years = 42 months
Rate of interest (r) = 12% p.a.
Amount of maturity = ₹ 10206 ……… (i)

Amount of each installment = ₹ 200
Question 6.
(i) Puneet has a Recurring Deposit Account in the Bank of Baroda and deposits ₹ 140 per month for 4 years If he gets ₹ 8,092 on maturity, find the rate of interest given by the bank.
(ii) David opened a Recurring Deposit Account in a bank and deposited ₹ 300 per month for two years. If he received ₹ 7725 at the time of maturity, find the rate of interest per annum. (2008)
Solution:
(i) Recurring deposit per month = ₹ 140
Period (n) = 4 years = 48 months
Let Rate of interest (r) = r % p.a.
Amount of maturity = ₹ 8,092
Total principal for one month


Question 7.
Amit deposited ₹ 150 per month in a bank for 8 months under the Recurring Deposits Scheme. What will be the maturity value of his deposits, if the rate of interest is 8% per annum and interest is calculated at the end of every month ? [I.C.S.E. 2001]
Solution:
Amount of Recurring deposit = ₹ 150
Period (n) = 8 months
Rate of interest (r) = 8% p.a.
Total principal for one month
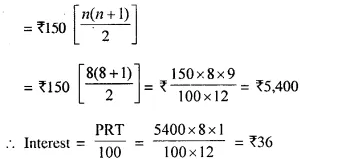
Amount of maturity value = ₹ 150 x 8 + ₹ 36 = ₹ 1,200 + ₹ 36 = ₹ 1,236
Question 8.
Mrs. Geeta deposited ₹ 350 per month in a bank for 1 year and 3 months under the Recurring Deposit Scheme. If the maturity value of her deposits is ₹ 5,565; find the rate of interest per annum.
Solution:
Amount of recurring deposit per month = ₹ 350
Period (n) = 1 year 3 months = 15 months
Let rate of interest = r % p.a.
Amount of maturity = ₹ 5565
Amount of interest = ₹ 5,565 – ₹ 350 x 15 = ₹ 5,565 – 5,250 = ₹ 315 ….(i)
Now, total principal for one month

Question 9.
A recurring deposit account of ₹ 1,200 per month has a maturity value of ₹ 12,440. If the rate of interest is 8% and the interest is calculated at the end of every month; find the time (in months) of this Recurring Deposit Account.
Solution:
Amount of recurring deposit per month = ₹ 1,200
Rate of interest (r) = 8% p.a.
Let period = n months
Amount of maturity = ₹ 12,440
Amount of interest = ₹ 12440 – ₹ 1200 x n ….(i)
Total principal for one month
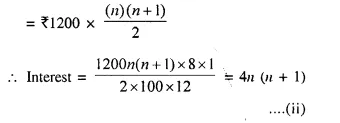
from (i) and (ii), we get,
4n (n + 1) = 12440 – 1200n
⇒ 4n² + 4n = 12440 – 1200n
⇒ 4n² + 1204n – 12440 = 0
Dividing by 4,
⇒ n² + 301n – 3110 = 0
⇒ n² + 311n – 10n – 3110 = 0
⇒ n (n + 311) – 10 (n + 311) = 0
⇒ (n + 311) (n – 10) = 0
Given n + 311 = 0, then n = – 311 Which is not possible,
or n – 10 = 0, then n = 10
Period = 10 months.
Question 10.
Mr. Gulati has a Recurring Deposit Account of ₹ 300 per month. If the rate of interest is 12% and the maturity value of this account is ₹ 8,100; find the time (in years) of this Recurring Deposit Account.
Solution:
Amount of recurring deposit per month = ₹ 300
Let Period = n months
Rate of interest (r) = 12% p.a.
Amount of maturity = ₹ 8,100
Interest = 8,100 – 300 x n ……. (i)
Total principal for 1 month
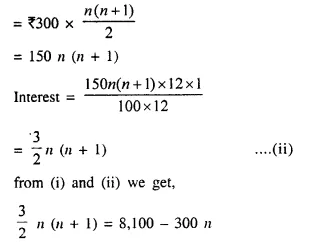
⇒ 3n (n + 1) = 16,200 – 600 n
⇒ 3n² + 3n = 16,200 – 600 n
⇒ 3n² + 603n – 16,200 = 0
Dividing by 3, we get,
⇒ n² + 201n – 5,400 = 0
⇒ n² + 225n – 24n – 5,400 = 0
⇒ n(n + 225) – 24 (n + 225) = 0
⇒ (n + 225) (n – 24) = 0
Either n + 225 = 0, then n = – 225 Which is not possible
or n – 24 = 0, then n = 24
Period = 24 months or 2 years.
Question 11.
Mr. Gupta opened a recurring deposit account in a bank. He deposited ₹ 2,500 per month for two years. At the time of maturity he got ₹ 67,500. Find :
(i) the total interest earned by Mr. Gupta.
(ii) the rate of interest per annum. (2010)
Solution:
(i) Total amount deposited by Mr. Gupta in 24 months = ₹ 2500 x 24 = ₹ 60,000
Maturity amount = ₹ 67,500
Total interest earned by Mr. Gupta = ₹ 67,500 – ₹ 60,000 = ₹ 7,500
(ii) Total principal for 1 month

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 2 Banking Ex 2A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.