Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Ex 21A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Prove the following Identities :
Question 1.

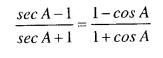
Solution:

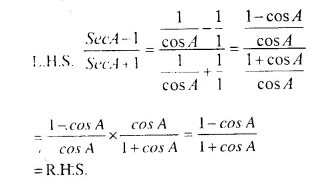
Question 2.

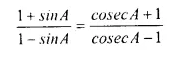
Solution:

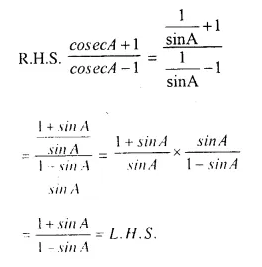
Question 3.

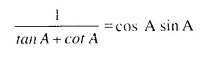
Solution:

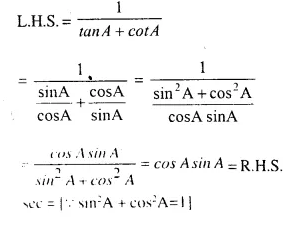
Question 4.

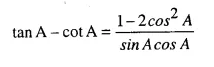
Solution:

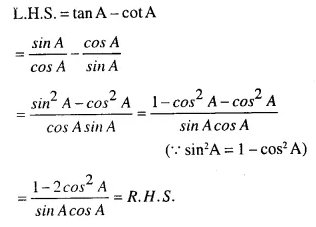
Question 5.
sin⁴A – cos⁴ A = 2 sin²A-1 
Solution:
L.H.S. = sin⁴ A – cos⁴A = (sin²A)²-(cos²A)²
= (sin²A + cos²A) (sin²A – cos²A)     [(a² – b² = (a + b) (a – b)]
= 1 (sin² A – cos²A) [∵ sin²A + cos²A = 1]
= sin² A – (1- sin²A) (∵ cos²A = 1 – sin²A)
= sin² A – 1 + sin² A
= 2 sin²A-1 = R.H.S.

Question 6.
(1 – tan A)² + (1 + tanA)² = 2sec²A
Solution:
LHS = (1 -tanA)² + (1 +tanA)²
= 1 + tan² A- 2 tan A + 1 + tan² A + 2 tanA
= 2 + 2 tan² A = 2 (1+tan²A)
= 2 sec²A (∵ l+tan²A=sec²A)
= R.H.S.

Question 7.
Cosec⁴ A – cosec² A = cot⁴ A + cot² A
Solution:
L.H.S. = cosec⁴ A -cosec² A
= (cosec²A)² – cosec²A
= (1 + cot²A)² – (1 + cot²A)
= 1 + cot⁴ A + 2 cot²A – 1- cot²A
= cot⁴ A + cot² A = R.H.S.

Question 8.
sec A (1-sin A) (sec A + tan A) = 1
Solution:

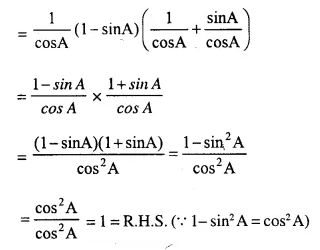
Question 9.
cosec A (1 + cos A) (cosec A – cot A) = 1
Solution:

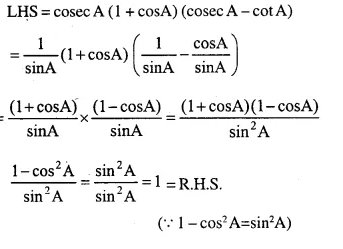
Question 10.
sec² A + cosec²A = sec² A cosec² A
Solution:

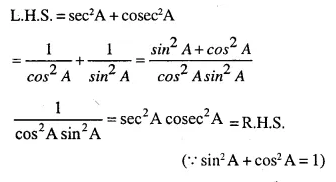
Question 11.

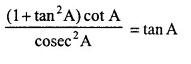
Solution:

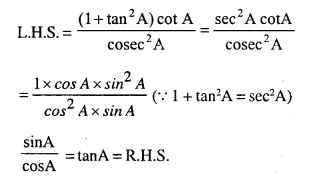
Question 12.
tan²A – sin²A = tan² A. sin² A
Solution:

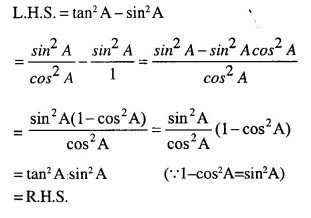
Question 13.
cot² A – cos² A = cos² A. cot² A
Solution:

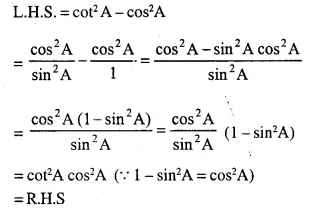
Question 14.
(cosecA + sinA) (cosec A – sinA) = cot² A + cos²A
Solution:
L.H.S. = (cosec A + sin A) (cosec A – sin A)
= (cosec²A – sin² A) [∵ (a + b) (a – b) = a²– b²]
= 1 + cot² A – sin² A = cot² A + 1 – sin²A
= cot² A + cos² A (∵ 1-sin²A = cos² A)
= R.H.S.

Question 15.
(sec A – cosA) (sec A + cosA) = sin² A + tan²A
Solution:
L.H.S. = (sec A-cos A) (sec A + cos A)
= sec² A – cos² A
= 1 + tan²A-cos² A
= 1-cos² A + tan² A
= sin² A + tan² A  (∵ 1- cos²A=sin²A)
= R.H.S.

Question 16.
(cos A + sin A)² + (cos A – sin A)² = 2
Solution:
LHS = (cos A + sin A)² + (cos A – sin A)²
= cos² A + sin² A + 2 cos A sin A + cos² A + sin² A – 2 cos A sin A
= 2 sin² A + 2 cos² A
= 2 (sin²A+cos²A)
= 2 x 1=2 = R.H.S. (∵ sin²A + cos² A = 1)

Question 17.
(cosec A – sin A) (sec A – cos A) (tan A + cot A) = 1
Solution:

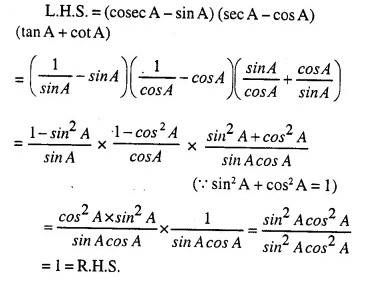
Question 18.

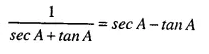
Solution:

Question 19.

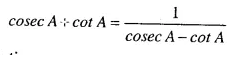
Solution:

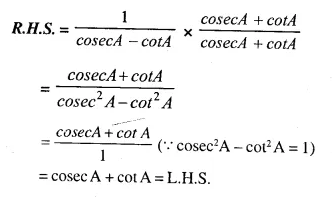
Question 20.

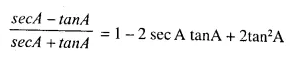
Solution:

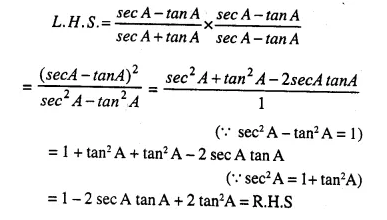
Question 21.
(sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A
Solution:
L.H.S. = (sin A + cosecA)² + (cosA+ secA)²
= sin² A + cosec² A + 2 sin A cosec A + cos² A + sec² A + 2 cos A sec A
= sin² A+cosec² A+2 sin A x \(\frac { 1 }{ sinA }\) + cos² A+sec²A + 2cosA x \(\frac { 1 }{ cosA }\)
= sin²A + cos² A + cosec² A + sec²A+ 2 + 2   (∵ sin² A + cos²A= 1)
= 1 +cosec²A + sec²A + 4
= (1 + cot² A) + (1 + tan² A) + 5 [∵ cosec²A = 1 + cot² A and sec² A = 1 + tan²A]
= 1 + cot² A + 1 + tan² A + 5
= 7 + tan²A + cot²A = R.H.S.

Question 22.
sec²A. cosec²A = tan²A + cot²A + 2
Solution:

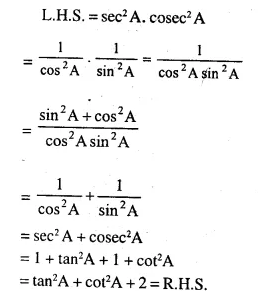
Question 23.

Solution:

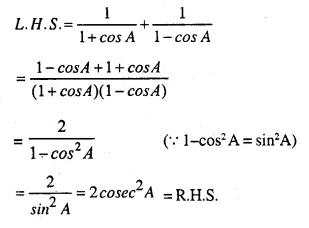
Question 24.

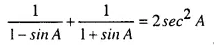
Solution:

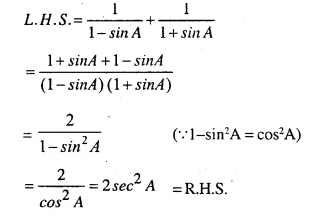
Question 25.

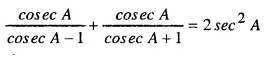
Solution:

Question 26.

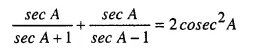
Solution:

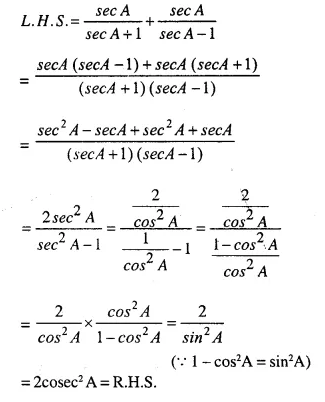
Question 27.

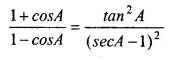
Solution:

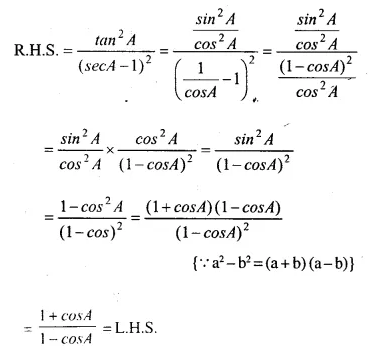
Question 28.

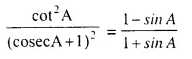
Solution:

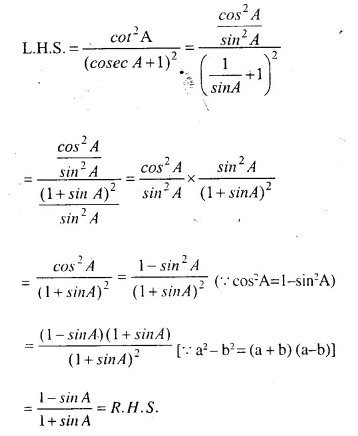
Question 29.

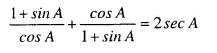
Solution:

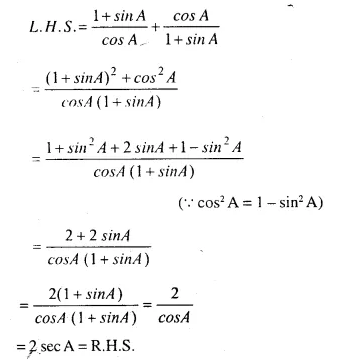
Question 30.

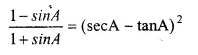
Solution:

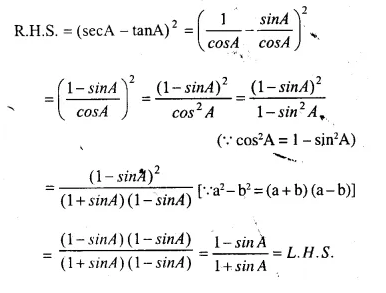
Question 31.

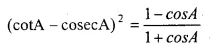
Solution:

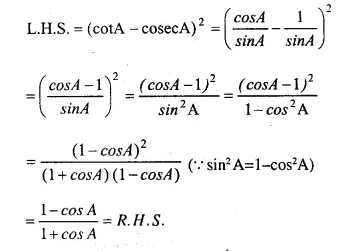
Question 32.

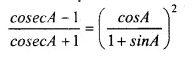
Solution:

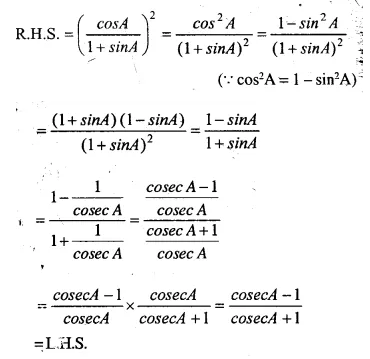
Question 33.

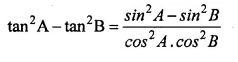
Solution:

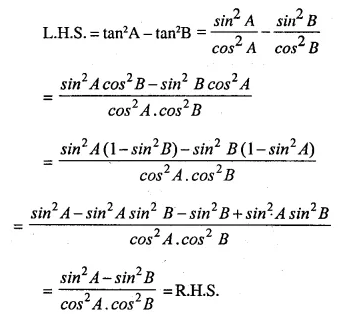
Question 34.

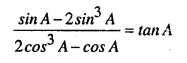
Solution:

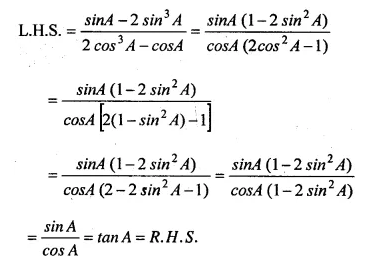
Question 35.

Solution:

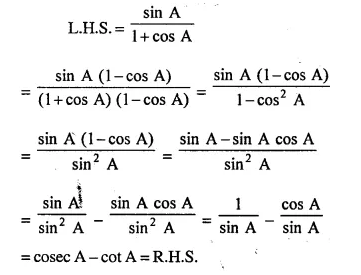
Question 36.

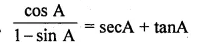
Solution:

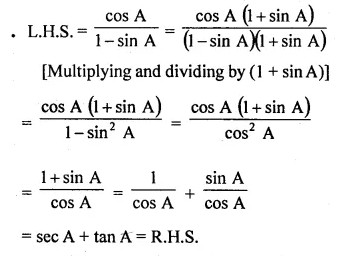
Question 37.

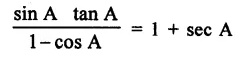
Solution:

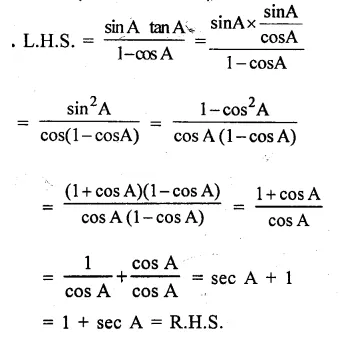
Question 38.
(1 +cot A-cosec A) (1 + tan A + sec A) = 2
Solution:

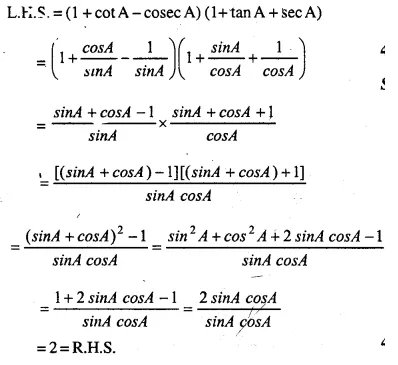
Question 39.

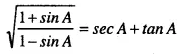
Solution:

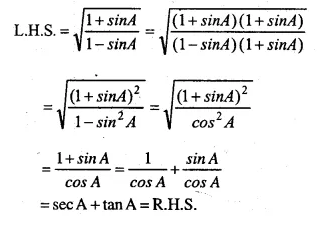
Question 40.

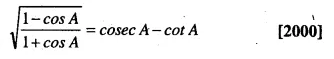
Solution:

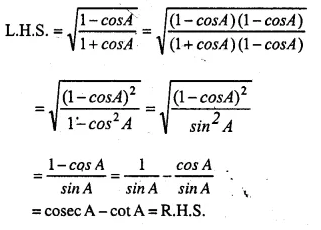
Question 41.

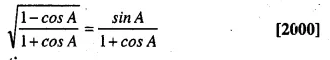
Solution:

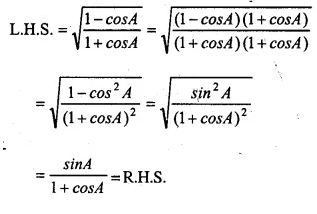
Question 42.

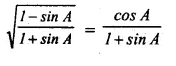
Solution:

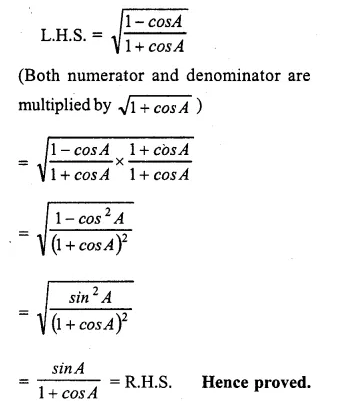
Question 43.

Solution:

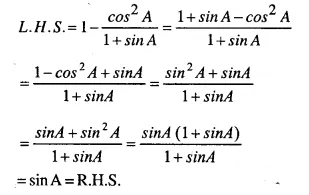
Question 44.

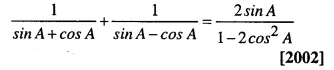
Solution:

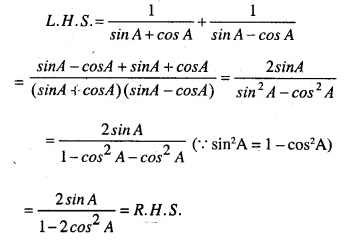
Question 45.

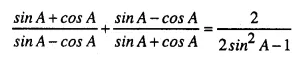
Solution:

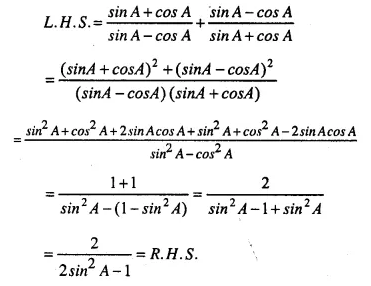
Question 46.

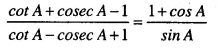
Solution:

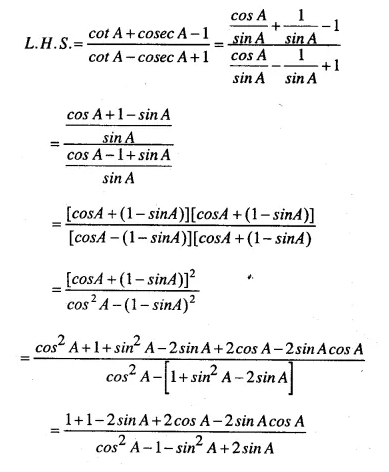
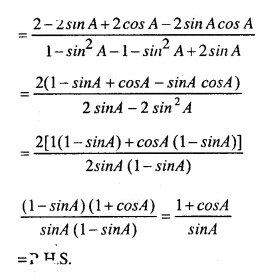
Question 47.

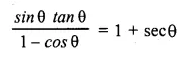
Solution:

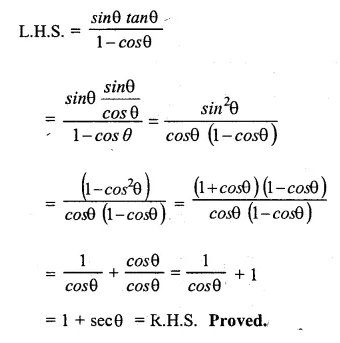
Question 48.

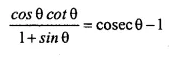
Solution:

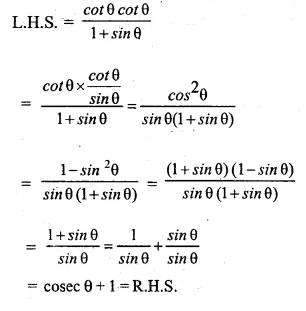
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.