Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Ex 21B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Question 1.
Prove that: 

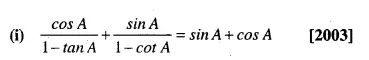
Solution:

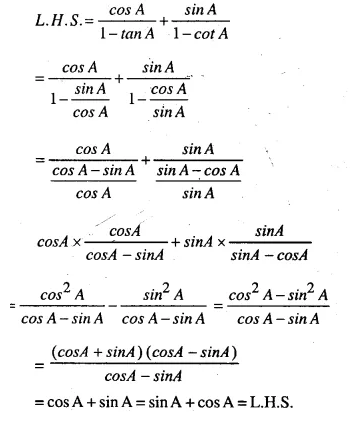
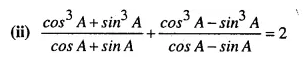
Solution:

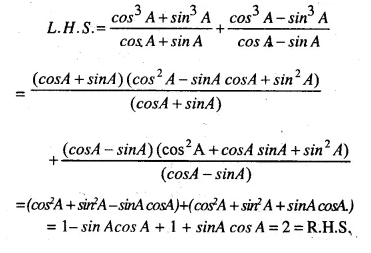
Solution:

Solution:

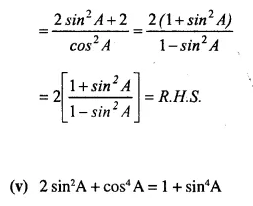
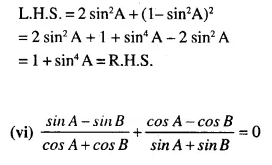
Solution:

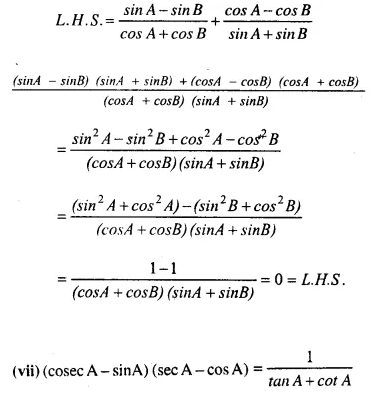
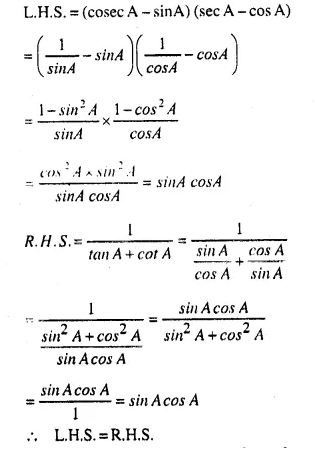
Solution:

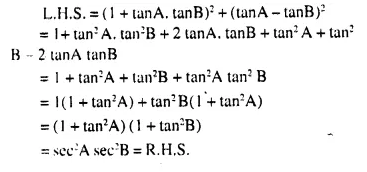
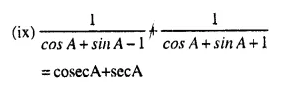
Solution:

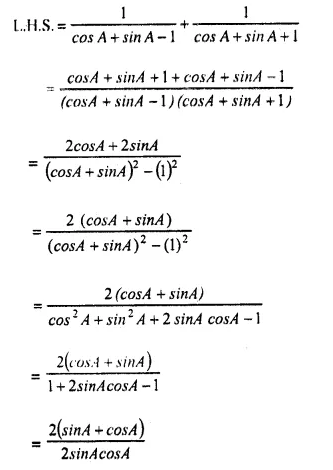
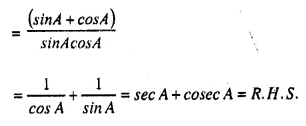
Question 2.
If xcosA + ysinA = m and xsinA-ycosA = n, then prove that: x²+y² = m² + n²
Solution:
x cos A + y sin A = m    …(i)
x sin A – y cos A = n     ….(ii)
squaring (i) and (ii)
x² cos² A + y² sin² A + 2 xy cosA sinA = m²
x² sin² A + y² cos² A – 2 xy cos A sin A = n²
Adding we get,
x² (sin² A + cos² A) + y² (sin² A + cos² A) = m²+n²
∴ x²+y² = m² + n²(∵ sin²A + cos²A= 1)
Hence proved.

Question 3.
If m = a sec A +b tan A and n=atanA + bsecA, then prove that: m²-n² = a²-b²
Solution:
m = asec A + btan A         ……(i)
n = a tan A + b sec A       …..(ii)
squaring (i) and (ii)
m² = a² sec² A + b² tan² A + 2ab sec A tan A
n² = a² tan² A + b² sec² A + 2 ab tan A sec A
Subtracting, we get
m² – n² = a² (sec² A – tan² A) + b² (tan² A – sec² A)
= a²x 1 +b²(-1) = a²-b² ( ∵ sec²A-tan²A= 1)  .
Henceproved

Question 4.
If x = r sin A cos B, y = r sin A sin B and z = r cos A, then prove that: x² + y² + z² = r.
Solution:
x = r sin A cos B      ….(i)
y = r sin A sin B      ….(ii)
z = r cosA               …….(iii)
Squaring, (i), (ii) & (iii)
x²=r² sin² A cos² B,
y² = r²sin²Asin²B,
z² = r²cos²A
Adding, we get,
x²+y² + z²=r² (sin²A cos²E + sin² A sin² B+cos²A)
= r[sin²A (cos² B + sin²B) + cos²A]
= r [sin² A x 1 + cos² A]
= r² [sin² A + cos² A] = r² x 1  = r²        ( ∵ sin² A + cos² A = 1)
Hence proved.

Question 5.
If sin A + cos A = m and sec A + cosec A=n, show that n (m²-1) = 2m
Solution:

Question 6.
If x = r cos A cos B, y = r cos A sin B and z = r sin A, show that x² + y² + z² = r²
Solution:
x = r cosAcosB              ….(i)
y = r cosAsinB             ….(ii)
z = r sinA                 ….(iii)
Squaring (i), (ii), (iii)
x² = r² cos² A cos² B, y² = r² cos² A sin²B
z² = r²sin²A
Adding, we get
x² + y² + z² = r² (cos² A cos²B + cos² A sin² B + sin² A)
= r² [cos² A (cos² B + sin²B) + sin² A]
= r²[cos²Ax 1+sin²A]
= r² (1) = r^{2    `}Hence proved.

Question 7.

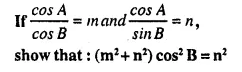
Solution:

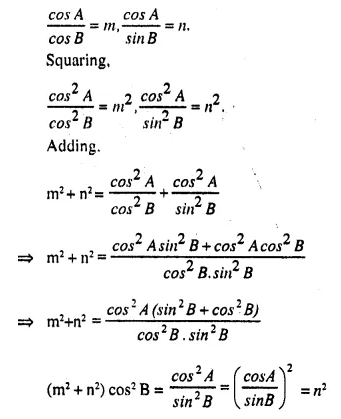
P.Q.

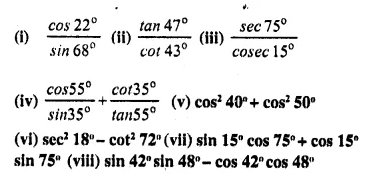
Solution:

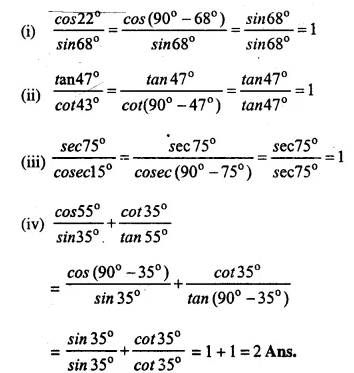
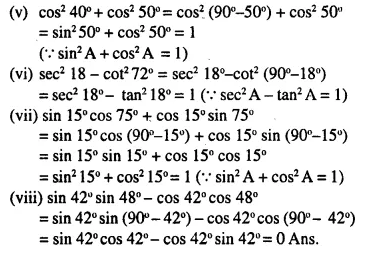
P.Q.
Evaluate:

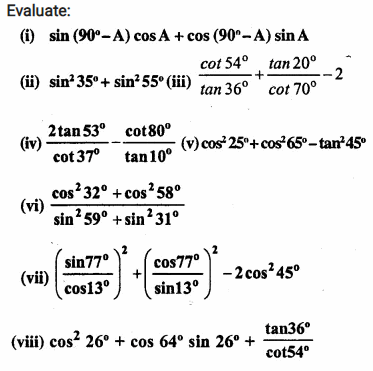
Solution:

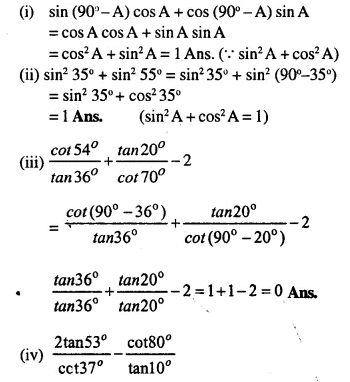
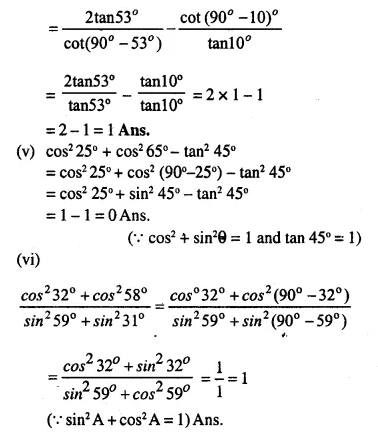
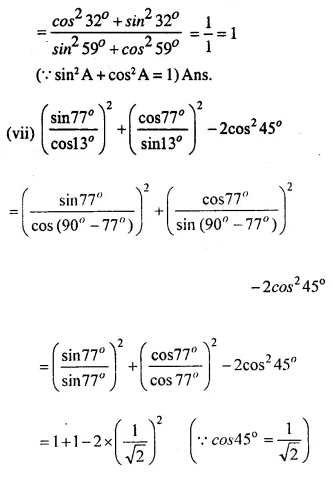
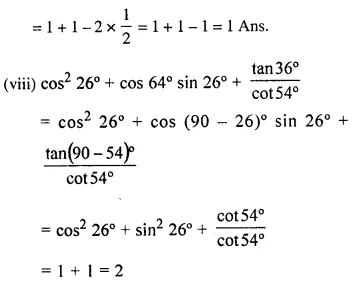
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.