Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Ex 21C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Question 1.
Show that:
(i) tan 10° tan 15° tan 75° tan 80° = 1
(ii) sin 42° sec 48°+cos 42° cosec 48°= 2

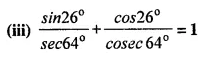
Solution:
(i) tan 10° tan 15° tan 75° tan 80°= 1
L.H.S. = tan 10° tan 15° tan 75° tan 80°
= tan (90° – 80°) tan (90° – 75°) tan 75° tan 80°
= cot 80° cot 75° tan 75° tan 80°
= tan 80° cot 80° x tan 75° cot 75°
= 1 x 1 = 1= R.H.S. (∵ tan A cot A = 1)
(ii) sin 42° sec 48°+ cos 42° cosec 48°= 2
L.H.S. = sin 42° sec 48°+ cos 42° cosec 48°
= sin 42° sec (90° – 42°) + cos 42° cosec (90° – 42°)
= sin 42° cosec 42°+ cos 42° sec 42°
=1 + 1=2 R.H.S. (∵ sin A cosec A=1, cos A sec A=1)

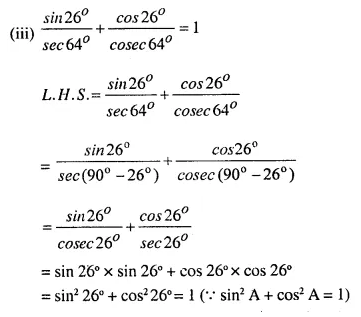
Question 2.
Express each of the following in terms of angles between 0°and 45°.
(i) sin 59° + tan 63°
(ii) cosec 68° + cot 72°
(iii) cos 74° + sec 67°
Solution:
(i) sin 59° + tan 63°
= sin (90° – 31°) + tan (90° – 27°)
= cos 31°+ cot 27°
(ii) cosec 68° + cot 72°
= cosec (90° – 22°) + cot (90° – 18°)
= sec 22°+ tan 18°
(iii) cos 74°+ sec 67°
= cos (90° – 16°) + sec (90° – 23°)
= sin 16°+ cosec 23°

Question 3.
Show that:

Solution:

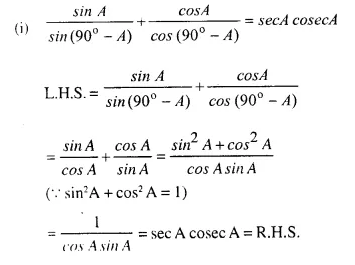
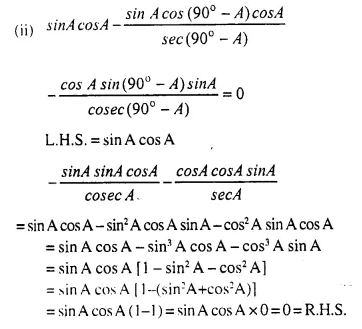
Question 4.
For triangle ABC, Show that:

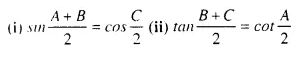
Solution:

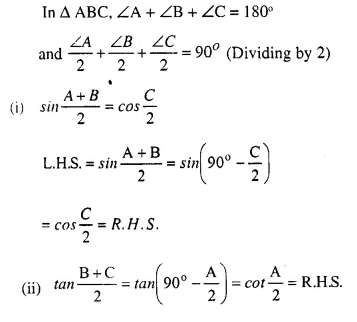
Question 5.
Evaluate:

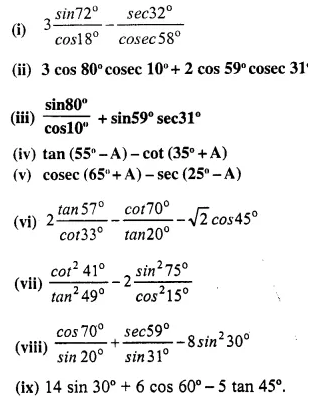
Solution:

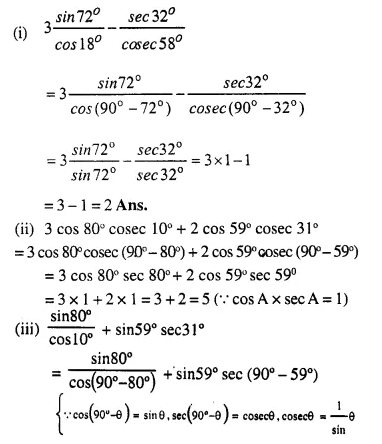
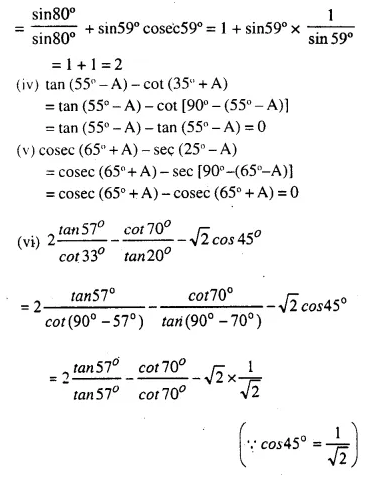
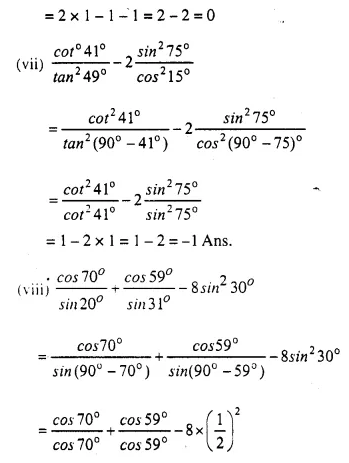
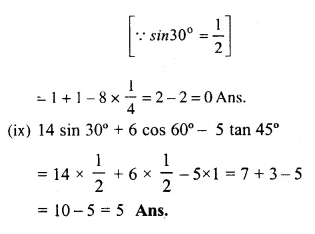
Question 6.

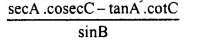
Solution:

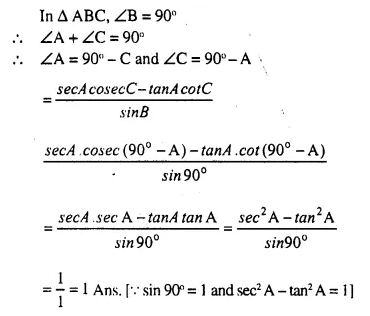
Question 7.
Find (in each case, given below) the value of x, if:
(i) sin x = sin 60° cos 30° – cos 60° sin 30°
(ii) sin x = sin 60° cos 30° + cos 60° sin 30°
(iii) cos x = cos 60° cos 30° – sin 60° sin 30°

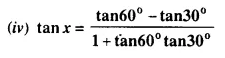
(v) sin 2x = 2 sin 45° cos 45° 
(vi) sin 3x = 2 sin 30° cos 30°
(vii) cos (2x – 6°) = cos² 30° – cos² 60°
Solution:

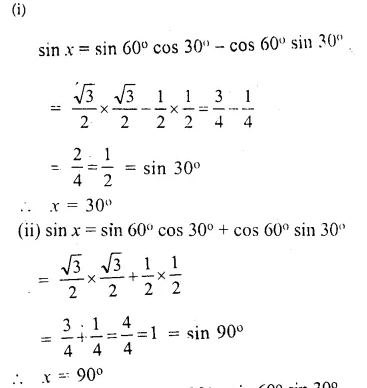
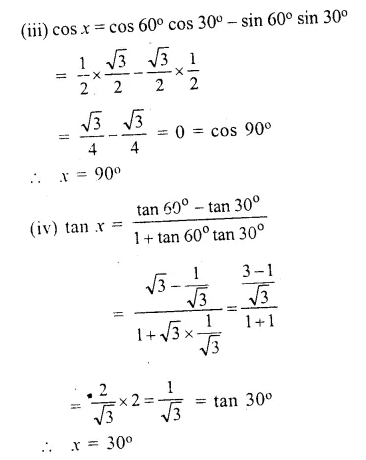
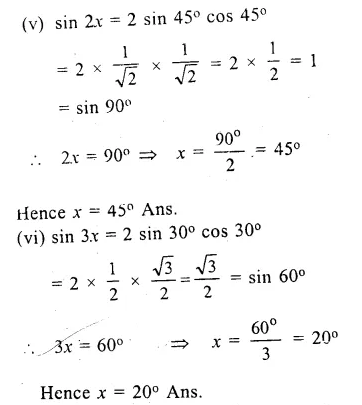
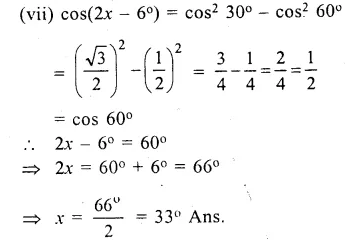
Question 8.
In each case, given below, find the value of angle A, where 0° ≤ A ≤ 90°.
(i) sin (90° – 3A). cosec 42° = 1
(ii) cos (90° – A). sec 77° = 1
Solution:

Question 9.
Prove that:

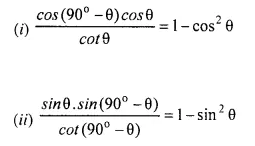
Solution:

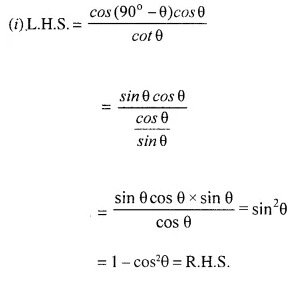
Question 10.
Evaluate:

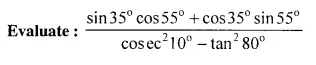
Solution:

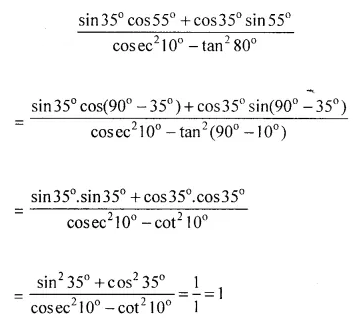
Question 11.
Without using trigonometric tables, evaluate sin² 34° + sin² 56° + 2 tan 18° tan 72° – cot² 30°.
Solution:

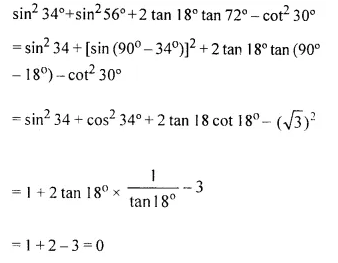
Question 12.
Without using trigonometrical tables, evaluate: cosec² 57° – tan² 33° + cos 44° cosec 46° – \( \sqrt{2} \) cos45°- tan² 60°
Solution:

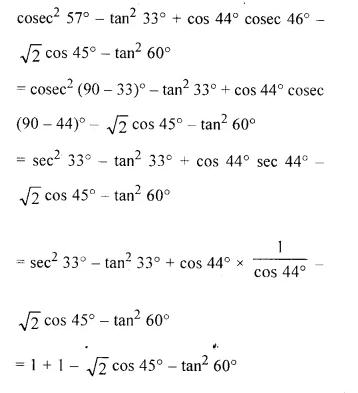
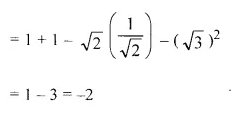
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.