Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Chapter 21 Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Ex 21E

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

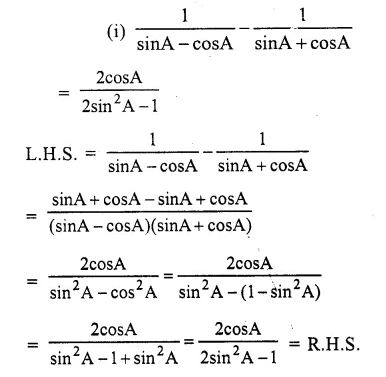
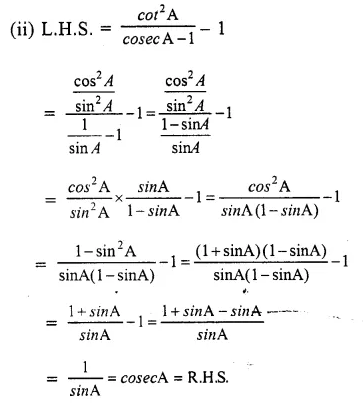
Question 1.
Prove the following identities :

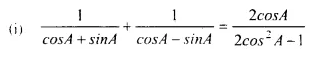
Solution:

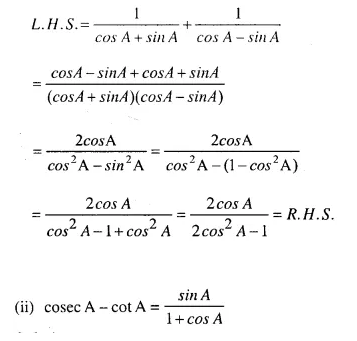
Solution:

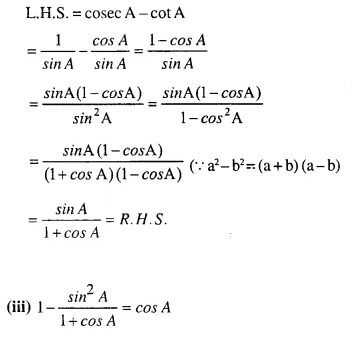
Solution:

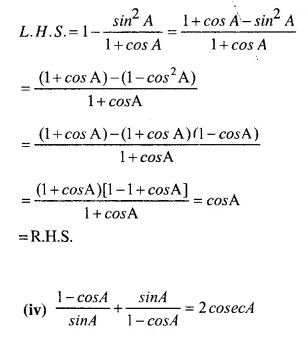
Solution:

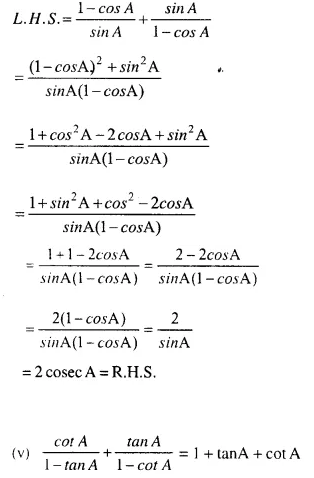
Solution:


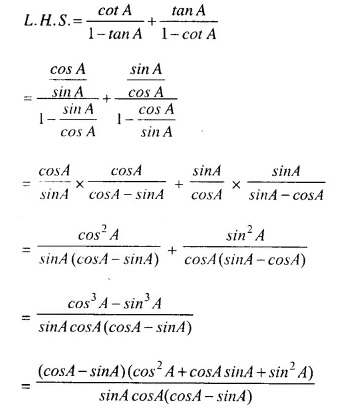
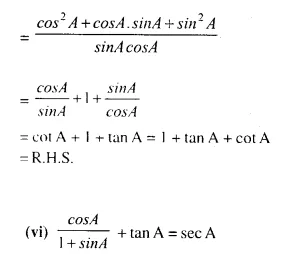
Solution:

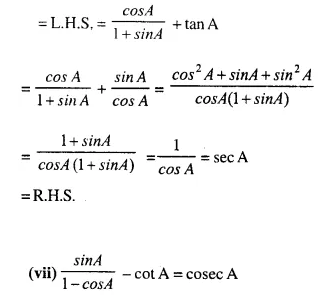
Solution:

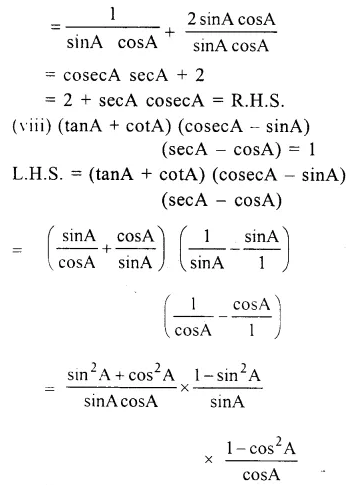
Solution:


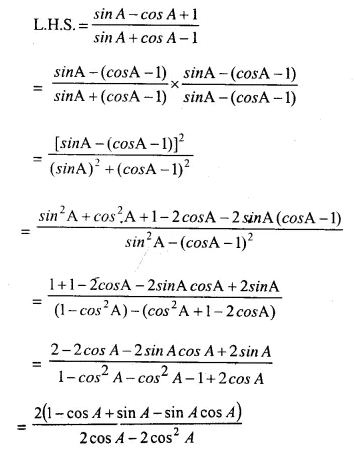
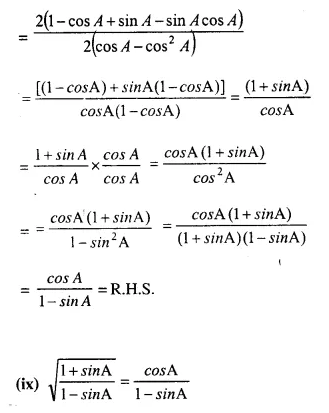
Solution:

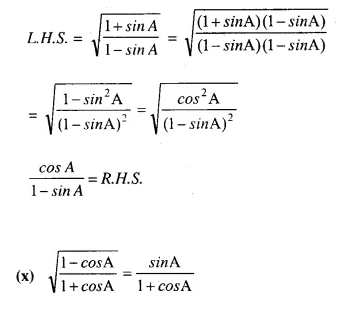
Solution:

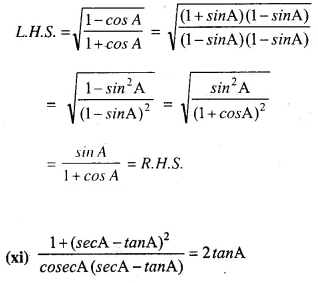
Solution:

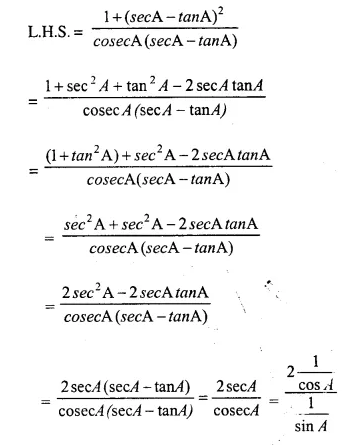
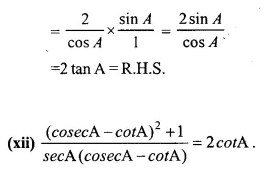
Solution:


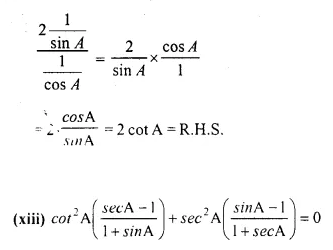
Solution:

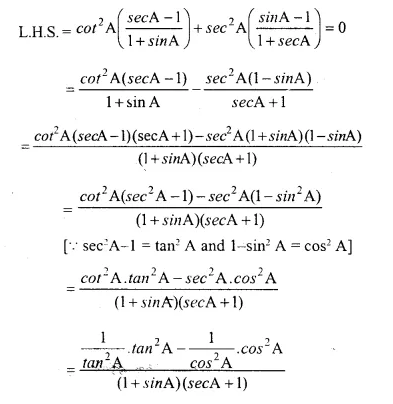
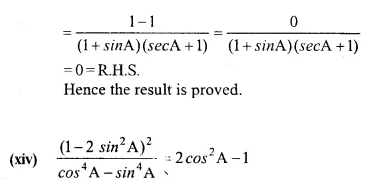
Solution:

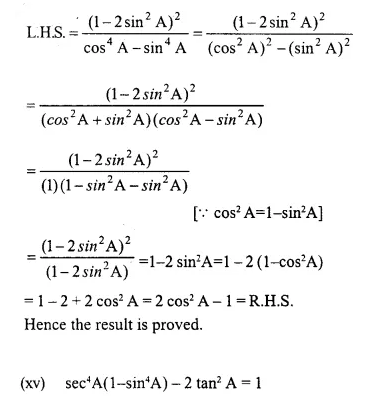
Solution:


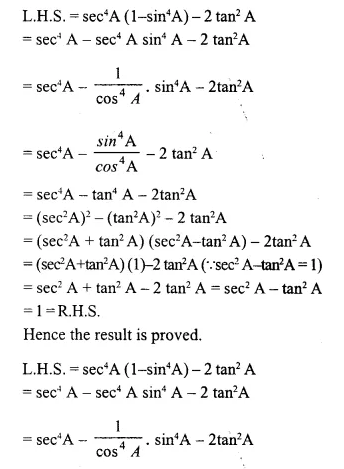
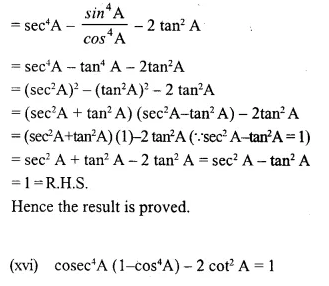
Solution:

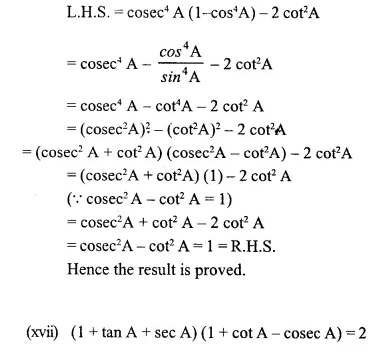
Solution:

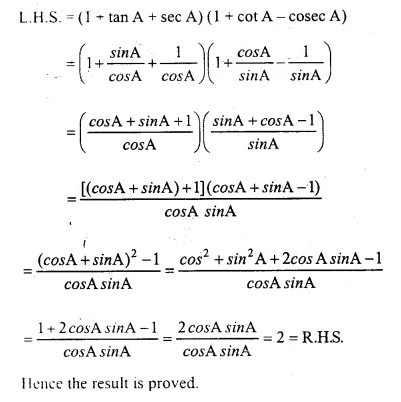
Question 2.
If sin A + cos A = p and sec A + cosec A = q then prove that: q(p² – 1) 2p
Solution:

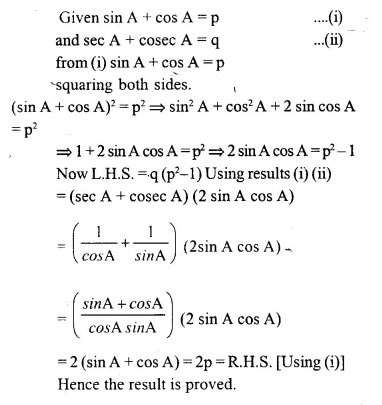
Question 3.

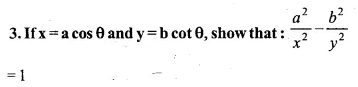
Solution:

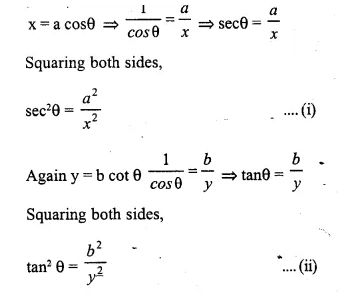
Question 4.

Solution:

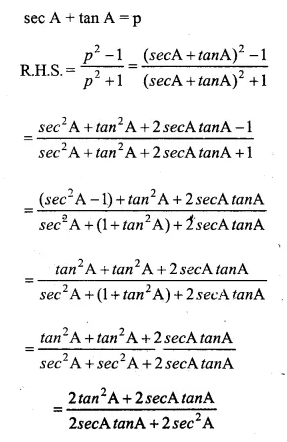
Question 5.
If tan A=n tan B and sin A=m sin B, prove that:

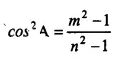
Solution:

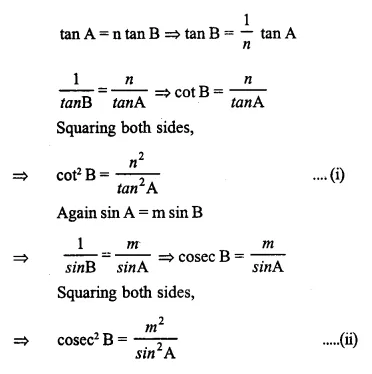
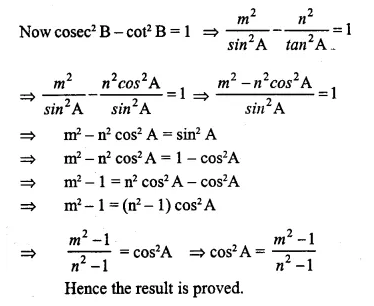
Question 6.
(i) If 2 sin A-1 = 0, show that:
sin 3 A = 3 sin A – 4 sin³ A.             [2001]
(ii) If 4cos² A-3 = 0, show that:
cos 3A = 4 cos³ A – 3 cos A
Solution:

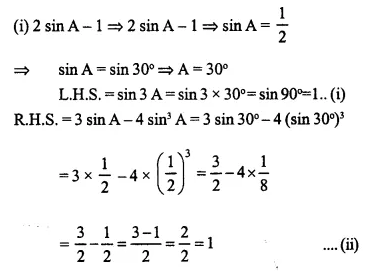
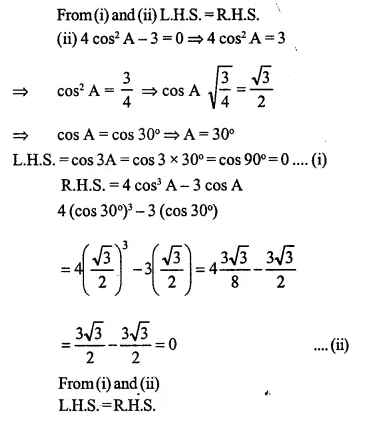
Question 7.
Evaluate:

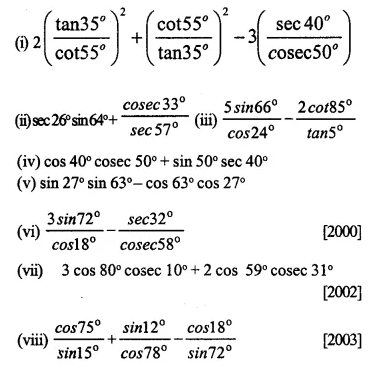
Solution:

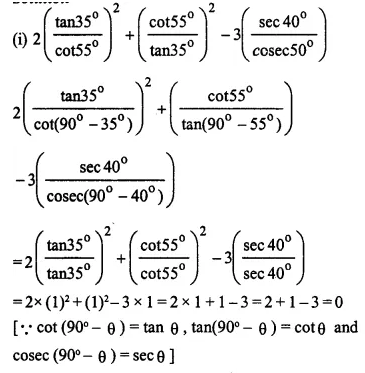
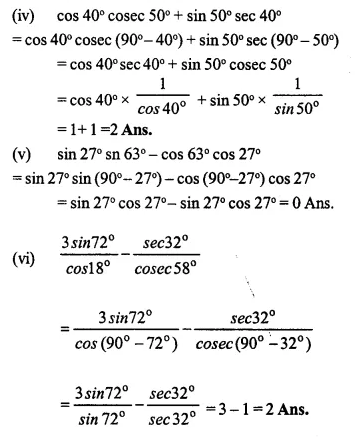
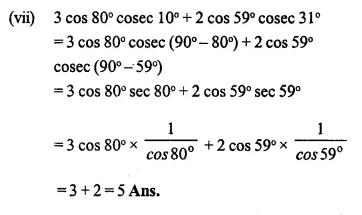
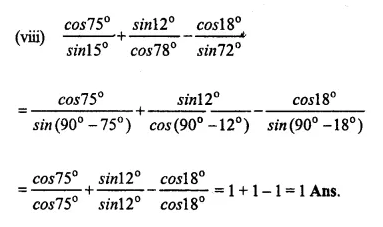
Question 8.
Prove that:

Solution:

Question 9.
If A and B are complementary angles, prove that:
(i) cot B + cos B sec A cos B (1 + sin B)
(ii) cot A cot B – sin A cos B – cos sin B = 0
(iii) cosec² A + cosec² B = cosec² A cosec² B

Solution:

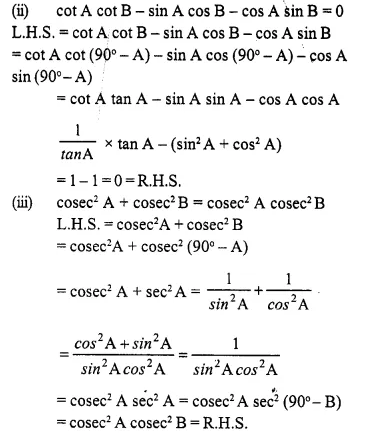
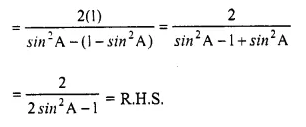
Question 10.
Prove that:


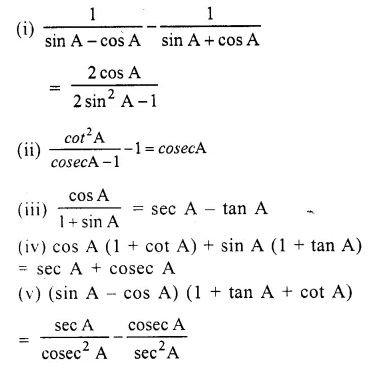
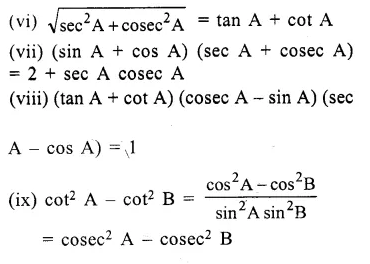
Solution:

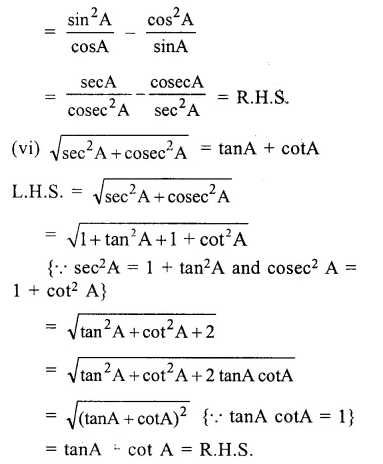
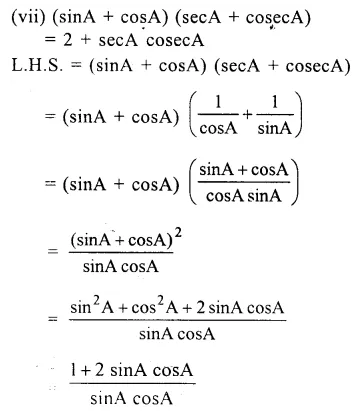
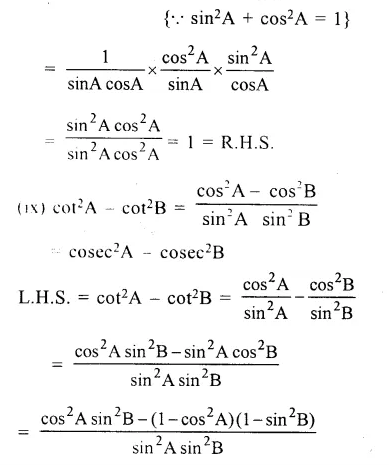
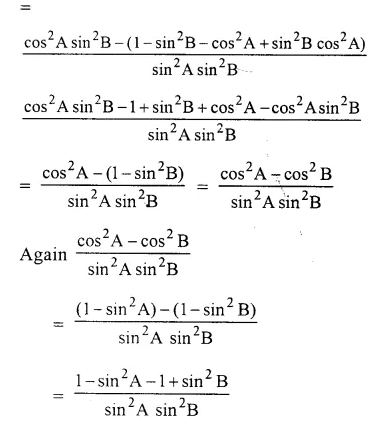
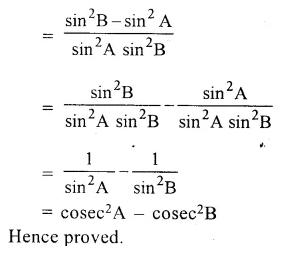
Question 11.
If 4 cos² A – 3 = 0 and 0° ≤ A ≤ 90°, then prove that : 
(i) sin 3A = 3 sinA – 4 sin³A
(ii) cos 3A = 4 cos³ A – 3 cos A
Solution:

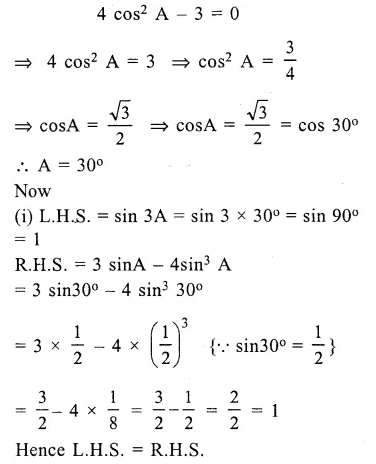
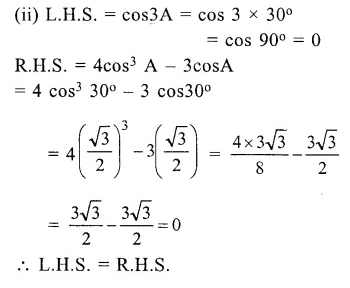
Question 12.
Find A, if 0° ≤ A ≤ 90° and :
(i) 2 cos² A – 1 = 0
(ii) sin 3A – 1 = 0
(iii) 4 sin² A – 3 = 0
(iv) cos² A – cos A = 0
(v) 2cos² A + cos A – 1 = 0
Solution:

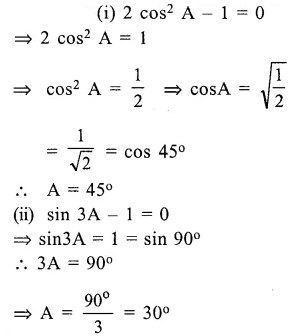
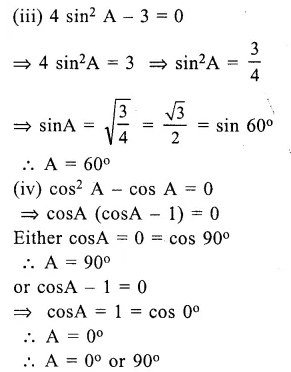
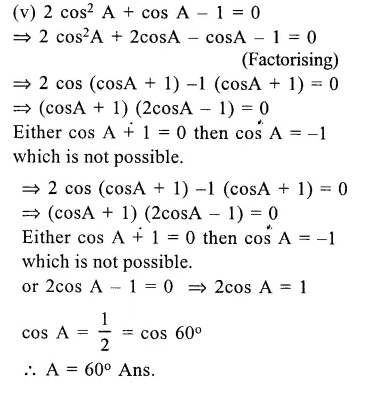
Question 13.
If 0° < A < 90° ; find A, if :

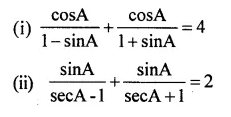
Solution:

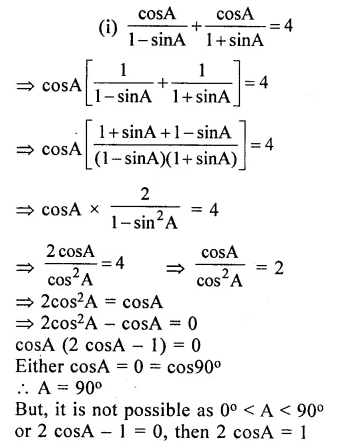
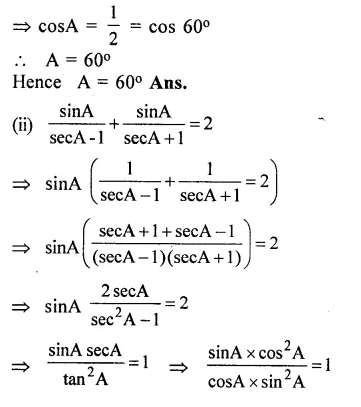
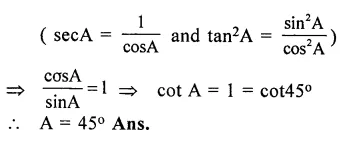
Question 14.
Prove that : (cosec A – sin A) (sec A – cos A) sec² A = tan A. (2011)
Solution:

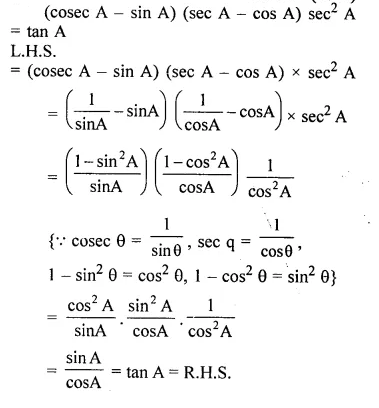
Question 15.
Prove the identity : (sin θ + cos θ) (tan θ + cot θ) = sec θ + cosec θ. (2014)
Solution:

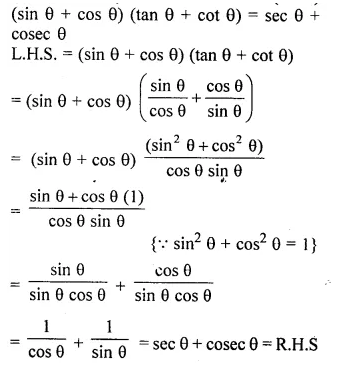
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.