Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4B

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations (In one variable) Ex 4B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4B

Question 1.
Represent the following inequalities on real number lines:
(i) 2x – 1 < 5
(ii) 3x + 1 ≥ – 5
(iii) 2 (2x – 3) ≤ 6
(iv) -4 < x < 4
(v) -2 ≤ x < 5 (vi) 8 ≥ x > -3
(vii) -5 < x ≤ -1
Solution:

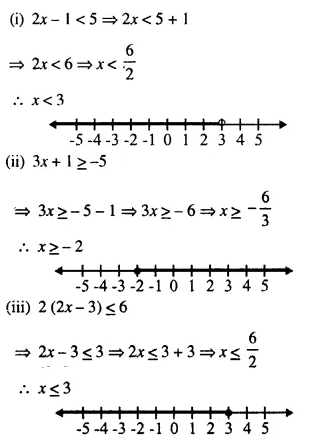
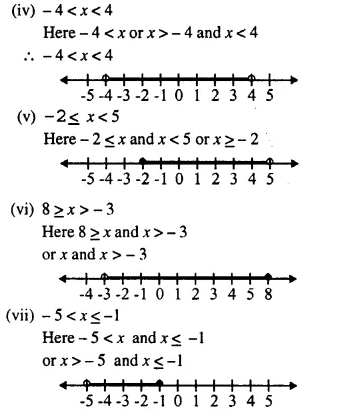
Question 2.
For each graph given below, write an inequation taking x as the variable :

Solution:

Question 3.
For the following inequations, graph the solution set on the real number line :
(i) – 4 ≤ 3x – 1 < 8
(ii) x – 1 < 3 – x ≤ 5
Solution:

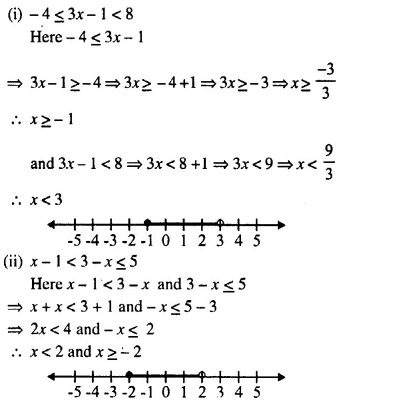
Question 4.
Represent the solution of each of the following inequalities on the real number line :
(i) 4x – 1 > x + 11
(ii) 7 – x ≤ 2 – 6x
(iii) x + 3 ≤ 2x + 9
(iv) 2 – 3x > 1 – 5x
(v) 1 + x ≥ 5x – 11
(vi) \(\frac { 2x + 5 }{ 2 }\) > 3x – 3
Solution:

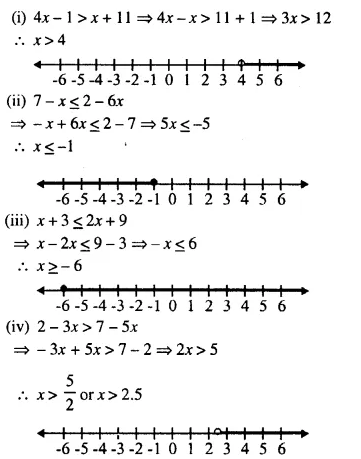
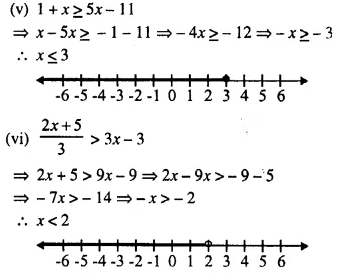
Question 5.
x ∈ {real numbers} and -1 < 3 – 2x ≤ 7, evaluate x and represent it on a number line.
Solution:

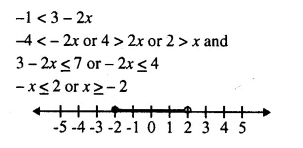
Question 6.
List the elements of the solution set of the inequation – 3 < x – 2 ≤ 9 -2x ; x ∈ N.
Solution:

Question 7.
Find the range of values of x which satisfies

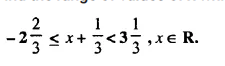
Graph these values of x on the number line.
Solution:

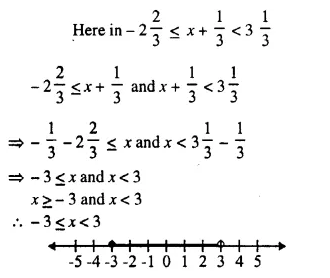
Question 8.
Find the values of x, which satisfy the inequation:

Graph the solution on the number line. (2007)
Solution:

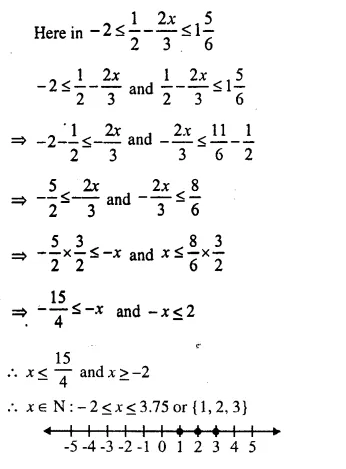
Question 9.
Given x ∈ {real numbers}, find the range of values of x for which – 5 ≤ 2x – 3 < x + 2 and represent it on a real number line.
Solution:

Question 10.
If 5x – 3 ≤ 5 + 3x ≤ 4x + 2, express it as a ≤ x ≤ b and then state the values of a and b.
Solution:
Here in, 5x – 3 ≤ 5 + 3x ≤ 4x + 2
⇒ 5x – 3 ≤ 5 + 3x and 5 + 3x ≤ 4x + 2
⇒ 5x – 3x ≤ 5 + 3 and 3x – 4x ≤ 2 – 5
⇒ 2x ≤ 8 and – x ≤ – 3
⇒ x ≤ 4 and x ≥ 3
Solution is 3 ≤ x ≤ 4
a = 3 and b = 4

Question 11.
Solve the following inequation and graph the solution set on the number line :
2x – 3 < x + 2 ≤ 3x + 5; x ∈ R.
Solution:

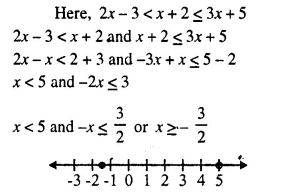
Question 12.
Solve and graph the solution set of:
(i) 2x – 9 < 7 and 3x + 9 ≤ 25; x ∈ R.
(ii) 2x – 9 ≤ 7 and 3x + 9 > 25; x ∈ I.
(iii) x + 5 ≥ 4 (x – 1) and 3 – 2x < -7; x ∈ R.
Solution:
(i) 2x – 9 < 7 and 3x + 9 ≤ 25; x ∈ R.

Question 13.
Solve and graph the solution set of:
(i) 3x – 2 > 19 or 3 – 2x ≥ – 7; x ∈ R.
(ii) 5 > p – 1 > 2 or 7 ≤ 2p – 1 ≤ 17; p ∈ R.
Solution:

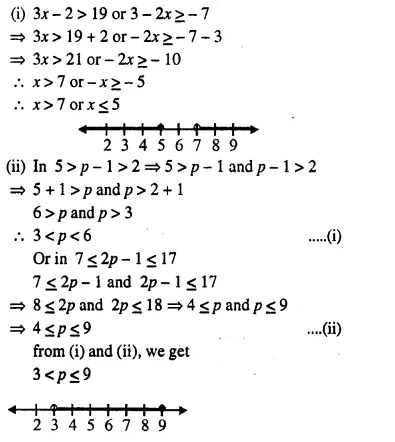
Question 14.
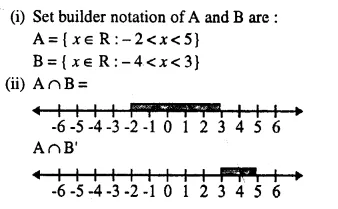
The diagram represents two inequations A and B on real number lines :

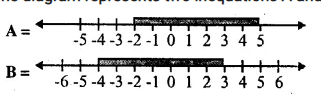
(i) Write down A and B in set builder notation.
(ii) Represent A ∩ B and A ∩ B’ on two different number lines.
Solution:

Question 15.
Use real number line to find the range of values of x for which :
(i) x > 3 and 0 < x < 6
(ii) x < 0 and -3 ≤ x < 1
(iii) -1 < x ≤ 6 and -2 ≤ x ≤ 3
Solution:

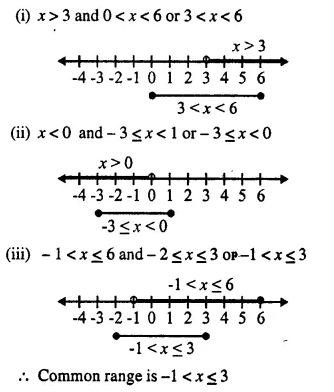
Question 16.
Illustrate the set {x : -3 ≤ x < 0 or x > 2 ; x ∈ R} on a real number line.
Solution:

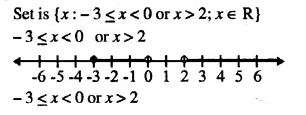
Question 17.
Given A = {x : -1 < x < 5, x ∈ R} and B = {x : – 4 < x < 3, x ∈ R}
Represent on different number lines:
(i) A ∩ B
(ii) A’ ∩ B
(iii) A – B
Solution:

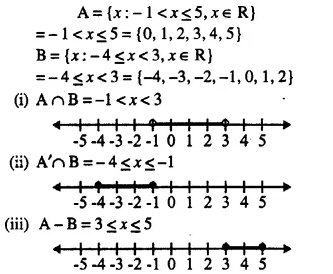
Question 18.
P is the solution set of 7x – 2 > 4x + 1 and Q is the solution set of 9x – 45 ≥ 5 (x – 5); where x ∈ R. Represent:
(i) P ∩ Q
(ii) P – Q
(iii) P ∩ Q’ on different number lines.
Solution:

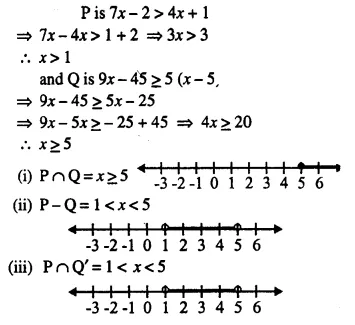
Question 19.
If P = {x : 7x – 4 > 5x + 2, x ∈ R} and Q = {x : x – 19 ≥ 1 – 3x , x ∈ R}: find the range of set P ∩ Q and represent it on a number line.
Solution:

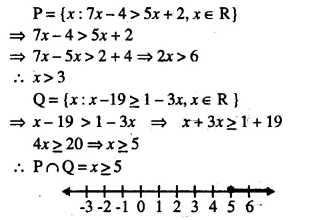
Question 20.
Find the range of values of x, which satisfy:

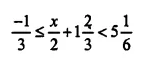
Graph, in each of the following cases, the values of x on the different real number lines:
(i) x ∈ W
(ii) x ∈ Z
(iii) x ∈ R.
Solution:

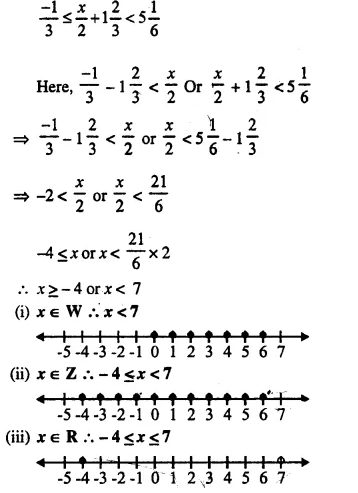
Question 21.
Given A = {x : – 8 < 5x + 2 ≤ 17, x ∈ I}, B = {x : -2 ≤ 7 + 3x < 17, x ∈ R}
Where R = {real numbers} and I = {integers}
Represent A an B is on two different number lines. Write down the elements of A ∩ B.
Solution:

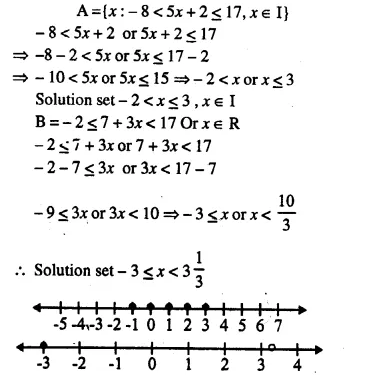
Question 22.
Solve the following inequation and represent the solution set on the number line 2x – 5 ≤ 5x + 4< 11, where x ∈ I.
Solution:

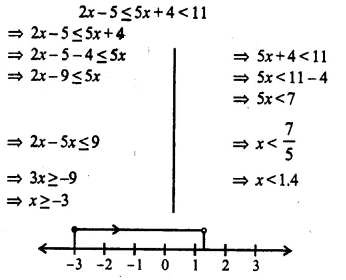
Question 23.
Given that x ∈ I, solve the inequation and graph the solution on the number line:

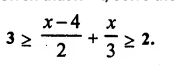
Solution:

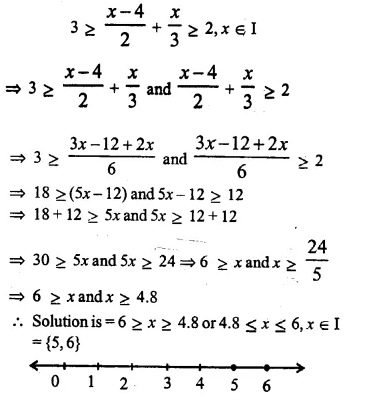
Question 24.
Given:
A = {x : 11x – 5 > 7x + 3, x ∈ R} and B = {x : 18x – 9 ≥ 15 + 12x, x ∈ R}.
Find the range of set A ∩ B and represent it on a number line. (2005)
Solution:

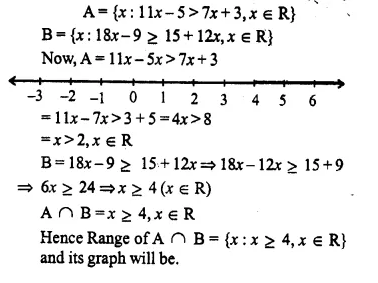
Question 25.
Find the set of values of x, satisfying:

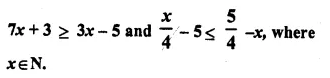
Solution:

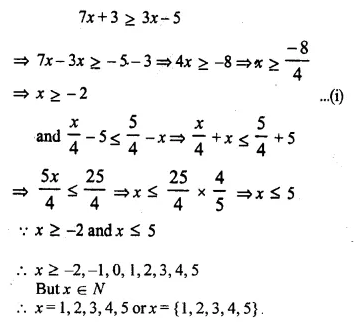
Question 26.

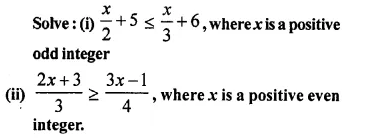
Solution:

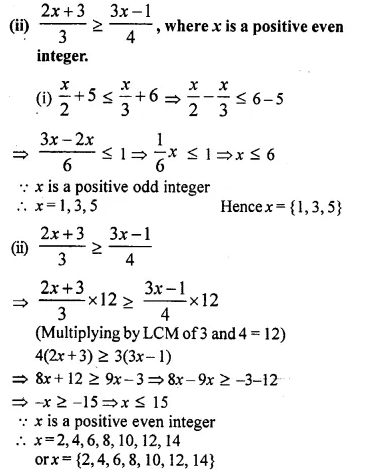
Question 27.
Solve the inequation:

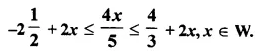
Graph the solution set on the number line.
Solution:

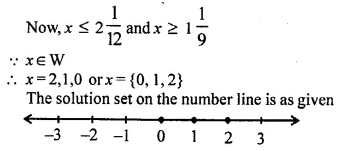
Question 28.
Find three consecutive largest positive integers such that the sum of one-third of first, one-fourth of second and one-fifth of third is atmost 20.
Solution:
Let first positive integer = x
Then, second integer = x + 1
and third integer = x + 2
According to the condition,

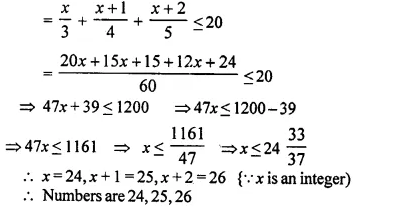
Question 29.
Solve the given inequation and graph the solution on the number line.
2y – 3 < y + 1 < 4y + 7; y ∈ R (2008)
Solution:

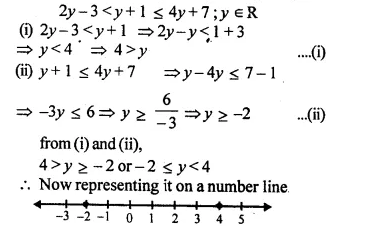
Question 30.
Solve the inequation:
3z – 5 ≤ z + 3 < 5z – 9; z ∈ R.
Graph the solution set on the number line.
Solution:

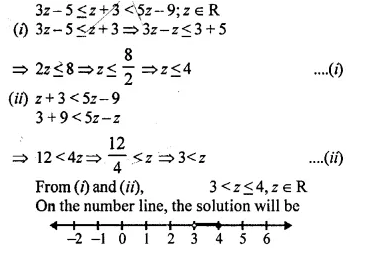
Question 31.
Solve the following inequation and represent the solution set on the number line.

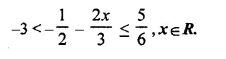
Solution:

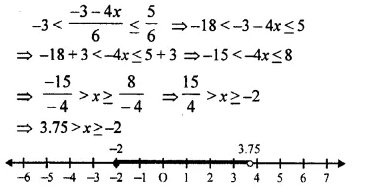
Question 32.
Solve the following inequation and represent the solution set on the number line:

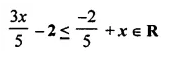
Solution:

Question 33.
Solve the following inequation, write the solution set and represent it on the number

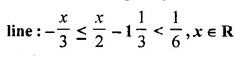
Solution:

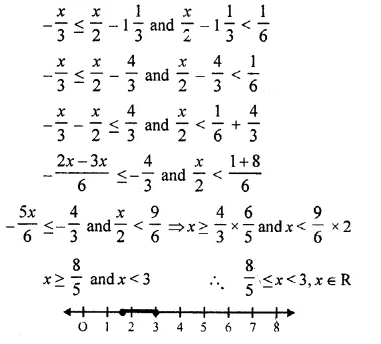
Question 34.

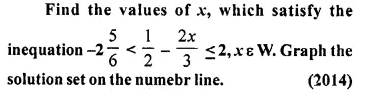
Solution:

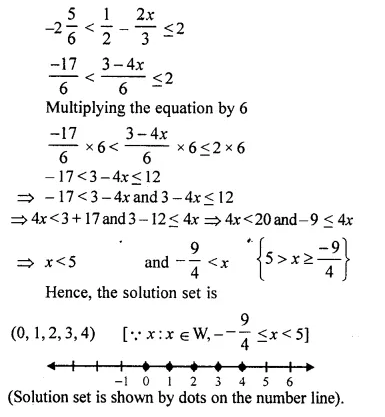
Question 35.
Solve the following inequation and write the solution set:
13x – 5 < 15x + 4 < 7x + 12, x ∈ R
Represent the solution on a real number line. (2015)
Solution:

Question 36.
Solve the following inequation, write the solution set and represent it on the number line.
-3 (x – 7) ≥ 15 – 7x > \(\frac { x + 1 }{ 3 }\), x ∈ R. (2016)
Solution:

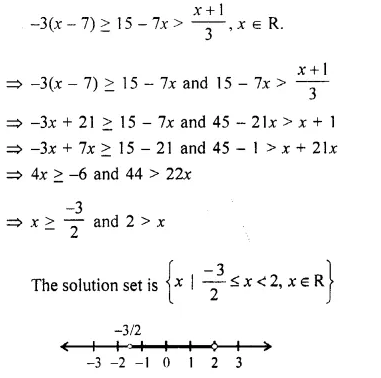
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 4 Linear Inequations Ex 4B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.