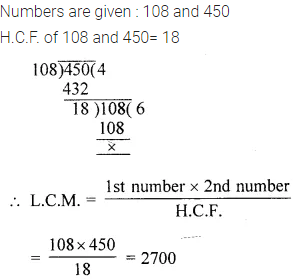Selina Concise Mathematics Class 6 ICSE Solutions Chapter 8 HCF and LCM

Selina Concise Mathematics Class 6 ICSE Solutions Chapter 8 HCF and LCM

Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 8 HCF and LCM

HCF and LCM Exercise 8A – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Write all the factors of :
(i) 15
(ii) 55
(iii) 48
(iv) 36
(v) 84
Solution:

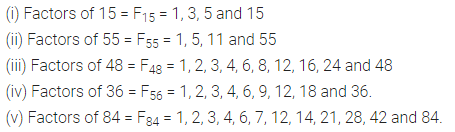
Question 2.
Write all prime numbers :
(i) less than 25
(ii) between 15 and 35
(iii) between 8 and 76
Solution:

Question 3.
Write the prime-numbers from :
(i) 5 to 45
(ii) 2 to 32
(iii) 8 to 48
(iv) 9 to 59
Solution:

Question 4.
Write the prime factors of:
(i) 16
(ii) 27
(iii) 35
(iv) 49
Solution:

Question 5.
If P_n means prime factors of n, find:
(i) p₆
(ii) P₂₄
(iii) p₅₀
(iv) P₄₂
Solution:

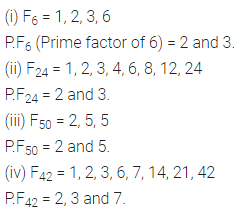
HCF and LCM Exercise 8B – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Using the common factor method, find the H.C.F. of :
(i) 16 and 35
(ii) 25 and 20
(iii) 27 and 75
(iv) 8, 12 and 18
(v) 24, 36, 45 and 60
Solution:

Question 2.
Using the prime factor method, find the H.C.F. of:
(i) 5 and 8
(ii) 24 and 49
(iii) 40, 60 and 80
(iv) 48, 84 and 88
(v) 12, 16 and 28
Solution:

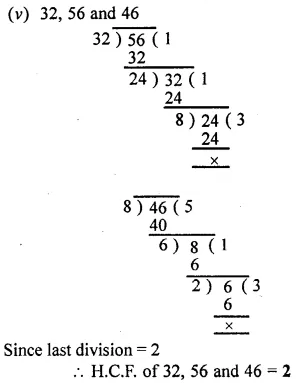
Question 3.
Using the division method, find the H.C.F. of the following :
(i) 16 and 24
(ii) 18 and 30
(iii) 7, 14 and 24
(iv) 70,80,120 and 150
(v) 32, 56 and 46
Solution:

Question 4.
Use a method of your own choice to find the H.C.F. of :
(i) 45, 75 and 135
(ii) 48, 36 and 96
(iii) 66, 33 and 132
(iv) 24, 36, 60 and 132
(v) 30, 60, 90 and 105
Solution:

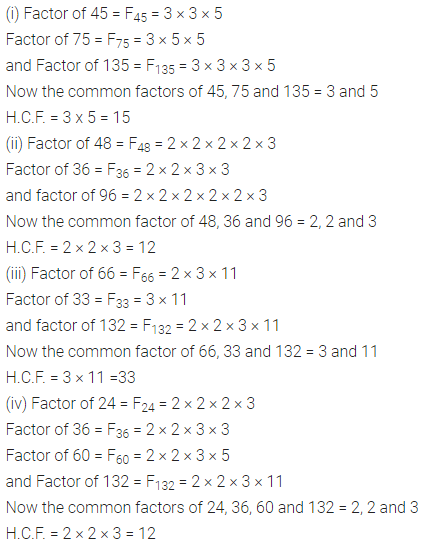
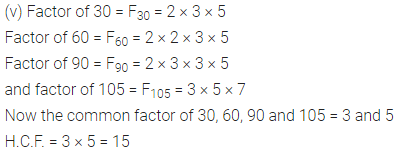
Question 5.
Find the greatest number that divides each of 180, 225 and 315 completely.
Solution:

Question 6.
Show that 45 and 56 are co-prime numbers.
Solution:

Question 7.
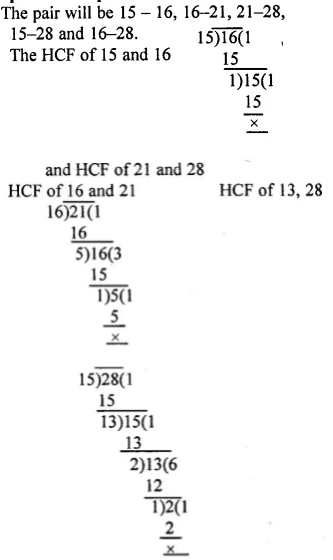
Out of 15, 16, 21 and 28, find out all the pairs of co-prime numbers.
Solution:

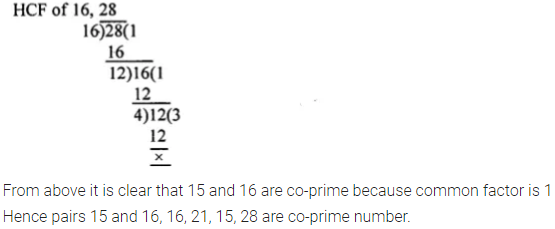
Question 8.
Find the greatest no. that will divide 93, 111 and 129, leaving remainder 3 in each case.
Solution:

HCF and LCM Exercise 8C – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Using the common multiple method, find the L.C.M. of the following :
(i) 8, 12 and 24
(ii) 10, 15 and 20
(iii) 3, 6, 9 and 12
Solution:

Question 2.
Find the L.C.M. of each the following groups of numbers, using
(i) the prime factor method and
(ii) the common division method :
(i) 18, 24 and 96
(ii) 100, 150 and 200
(iii) 14, 21 and 98
(iv) 22, 121 and 33
(v) 34, 85 and 51
Solution:

Question 3.
The H.C.F. and the L.C.M. of two numbers are 50 and 300 respectively. If one of the numbers is 150, find the other one.
Solution:

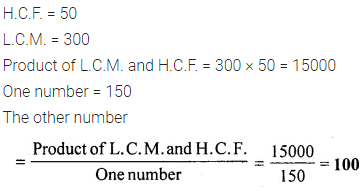
Question 4.
The product of two numbers is 432 and their L.C.M. is 72. Find their H.C.F.
Solution:

Question 5.
The product of two numbers is 19,200 and their H.C.F. is 40. Find their L.C.M.
Solution:

Question 6.
Find the smallest number which, when divided by 12, 15, 18, 24 and 36 leaves no remainder
Solution:

Question 7.
Find the smallest number which, when increased by one is exactly divisible by 12, 18, 24, 32 and 40
Solution:

Question 8.
Find the smallest number which, on being decreased by 3, is completely divisible by 18, 36, 32 and 27.
Solution:

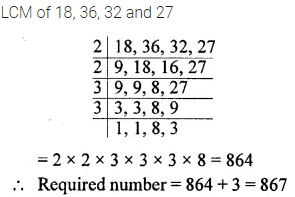
HCF and LCM Revision Exercise – Selina Concise Mathematics Class 6 ICSE Solutions

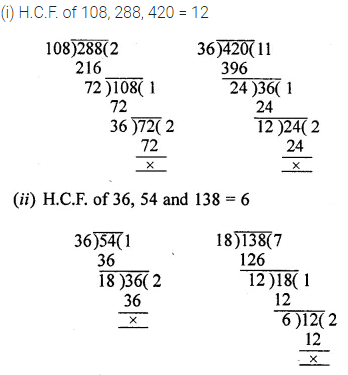
Question 1.
Find the H.C.F. of :
(i) 108, 288 and 420
(ii) 36, 54 and 138
Solution:

Question 2.
Find the L.C.M. of:
(i) 72, 80 and 252
(ii) 48, 66 and 120
Solution:

Question 3.
State true or false : Give an example.
(i) H.C.F. of two prime numbers is 1.
(ii) H.C.F. of two co-prime numbers is 1.
(iii) L.C.M. of two prime numbers is equal to their product.
(iv) L.C.M. of two co-prime numbers is equal to their product.
Solution:

Question 4.
The product of two numbers is 12096 and their H.C.F. is 36. Find their L.C.M.
Solution:

Question 5.
The product of the H.C.F. and the L.C.M. of two numbers is 1152. If one number is 48, find the other one.
Solution:

Question 6.
(i) Find the smallest number that is completely divisible by 28 and 42.
(ii) Find the largest number that can divide 28 and 42 completely.
Solution:

Question 7.
Find the L.C.M. of 140 and 168. Use the L.C.M. obtained to find the H.C.F. of the given numbers.
Solution:

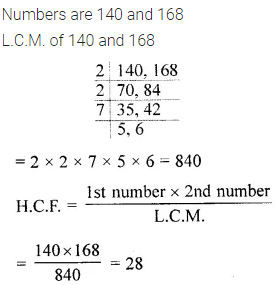
Question 8.
Find the H.C.F. of 108 and 450 and use the H.C.F. obtained to find the L.C.M. of the given numbers.
Solution:

Selina Concise Mathematics Class 6 ICSE Solutions