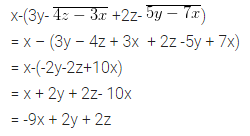Selina Concise Mathematics Class 7 ICSE Solutions Chapter 11 Fundamental Concepts

Selina Concise Mathematics Class 7 ICSE Solutions Chapter 11 Fundamental Concepts (Including Fundamental Operations)

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 11 Fundamental Concepts (Including Fundamental Operations)

Fundamental Concepts Exercise 11A – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Separate constant terms and variable terms from tile following :

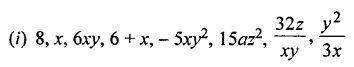
Solution:

Question 2.
Constant is only 8 others are variables
(i) 2x ÷ 15
(ii) ax+ 9
(iii) 3x² × 5x
(iv) 5 + 2a-3b
(v) 2y – \(\frac { 7 }{ 3 }\) z÷x
(vi) 3p x q ÷ z
(vii) 12z ÷ 5x + 4
(viii) 12 – 5z – 4
(ix) a³ – 3ab² x c
Solution:

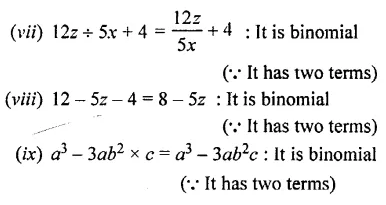
Question 3.
Write the coefficient of:
(i) xy in – 3axy
(ii) z² in p²yz²
(iii) mn in -mn
(iv) 15 in – 15p²
Solution:

Question 4.
For each of the following monomials, write its degree :
(i) 7y
(ii) – x²y
(iii) xy²z
(iv) – 9y²z³
(v) 3 m³n⁴
(vi) – 2p²q³r⁴
Solution:

Question 5.
Write the degree of each of the following polynomials :
(i) 3y³-x²y² + 4x
(ii) p³q² – 6p²q⁵ + p⁴q⁴
(iii) – 8mn⁶+ 5m³n
(iv) 7 – 3x²y + y²
(v) 3x – 15
(vi) 2y²z + 9yz³
Solution:

Question 6.
Group the like term together :
(i) 9x², xy, – 3x², x² and – 2xy
(ii) ab, – a²b, – 3ab, 5a²b and – 8a²b
(iii) 7p, 8pq, – 5pq – 2p and 3p
Solution:

Question 7.
Write numerical co-efficient of each of the followings :
(i) y
(ii) -y
(iii) 2x²y
(iv) – 8xy³
(v) 3py²
(vi) – 9a²b³
Solution:

Question 8.
In -5x³y²z⁴; write the coefficient of:
(i) z²
(ii) y²
(iii) yz²
(iv) x³y
(v) -xy²
(vi) -5xy²z
Also, write the degree of the given algebraic expression.
Solution:

EXERCISE 11 (B)

Question 1.
Fill in the blanks :
(i) 8x + 5x = ………
(ii) 8x – 5x =……..
(iii) 6xy² + 9xy² =……..
(iv) 6xy² – 9xy² = ………
(v) The sum of 8a, 6a and 5b = ……..
(vi) The addition of 5, 7xy, 6 and 3xy = …………
(vii) 4a + 3b – 7a + 4b = ……….
(viii) – 15x + 13x + 8 = ………
(ix) 6x²y + 13xy² – 4x²y + 2xy² = ……..
(x) 16x² – 9x² = and 25xy² – 17xy²=………

Solution :

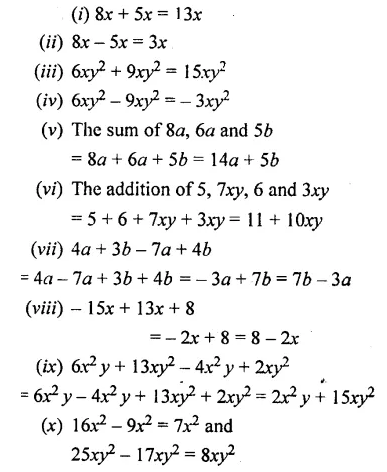
Question 2.
Add :
(i)- 9x, 3x and 4x
(ii) 23y², 8y² and – 12y²
(iii) 18pq – 15pq and 3pq

Solution:

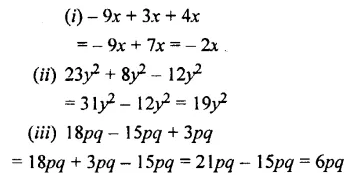
Question 3.
Simplify :
(i) 3m + 12m – 5m
(ii) 7n² – 9n² + 3n²
(iii) 25zy—8zy—6zy
(iv) -5ax² + 7ax² – 12ax²
(v) – 16am + 4mx + 4am – 15mx + 5am
Solution:

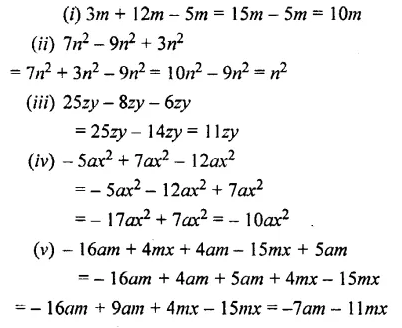
Question 4.
Add :
(i) a + b and 2a + 3b
(ii) 2x + y and 3x – 4y
(iii)- 3a + 2b and 3a + b
(iv) 4 + x, 5 – 2x and 6x
Solution:

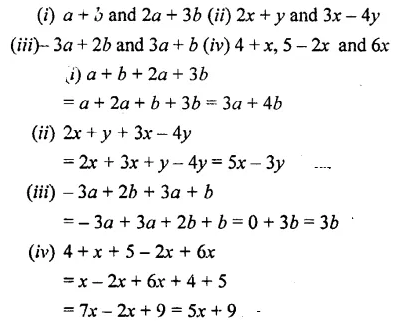
Question 5.
Find the sum of:
(i) 3x + 8y + 7z, 6y + 4z- 2x and 3y – 4x + 6z
(ii) 3a + 5b + 2c, 2a + 3b-c and a + b + c.
(iii) 4x²+ 8xy – 2y² and 8xy – 5y² + x²
(iv) 9x² – 6x + 7, 5 – 4x and 6 – 3x²
(v) 5x² – 2xy + 3y² and – 2x² + 5xy + 9y²
and 3x² -xy- 4y²
(vi) a² + b² + 2ab, 2b² + c² + 2bc
and 4c²-a² + 2ac
(vii) 9ax – 6bx + 8, 4ax + 8bx – 7
and – 6ax – 46x – 3
(viii) abc + 2 ba + 3 ac, 4ca – 4ab + 2 bca
and 2ab – 3abc – 6ac
(ix) 4a² + 5b² – 6ab, 3ab, 6a² – 2b²
and 4b² – 5 ab
(x) x² + x – 2, 2x – 3x² + 5 and 2x² – 5x + 7
(xi) 4x³ + 2x² – x + 1, 2x³ – 5x²– 3x + 6, x² + 8 and 5x³ – 7x
Solution:

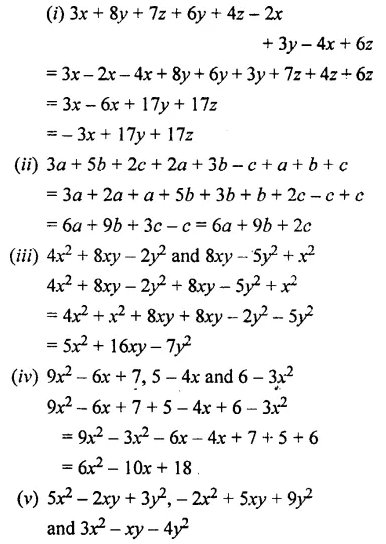
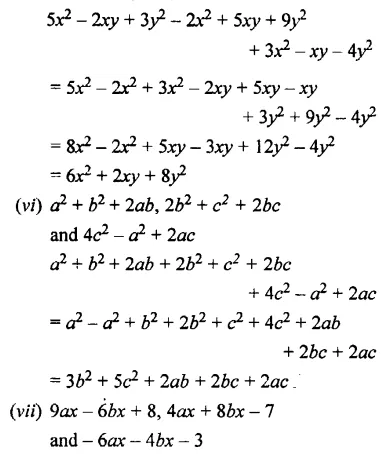
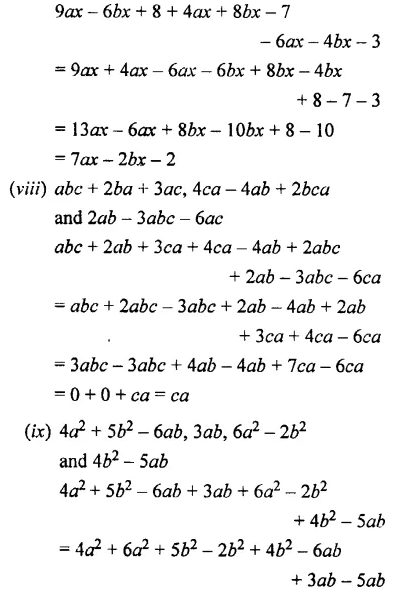
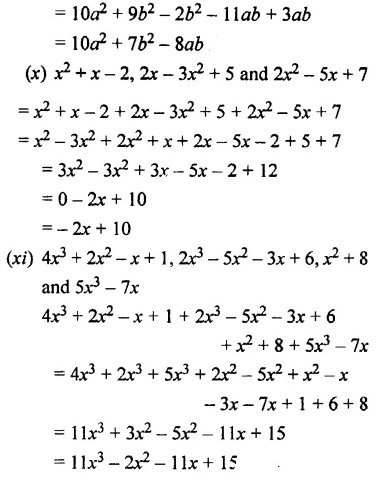
Question 6.
Find the sum of:
(i) x and 3y
(ii) -2a and +5
(iii) – 4x² and +7x
(iv) +4a and -7b
(v) x³+3x²y and 2y²
(vi) 11 and -by
Solution:

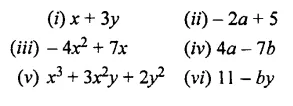
Question 7.
The sides of a triangle are 2x + 3y, x + 5y and 7x – 2y, find its perimeter.
Solution:

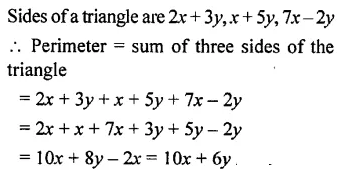
Question 8.
The two adjacent sides of a rectangle are 6a + 96 and 8a – 46. Find its, perimeter.
Solution

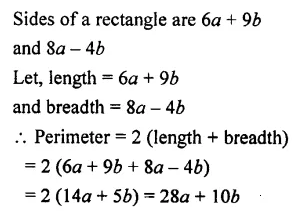
Question 9.
Subtract the second expression from the first:

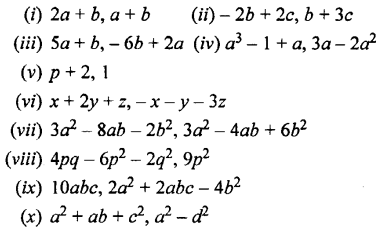
Solution:

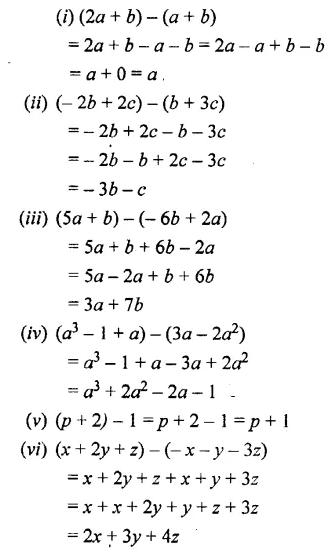
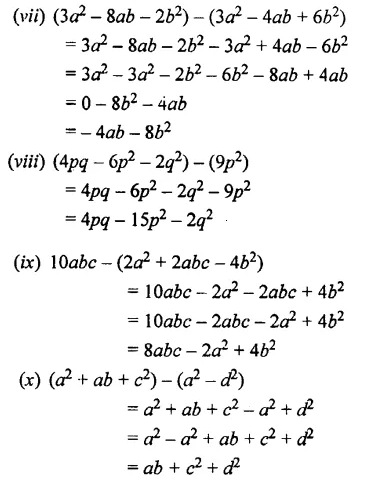
Question 10.
Subtract:

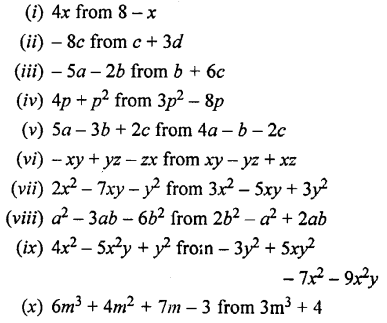
Solution:

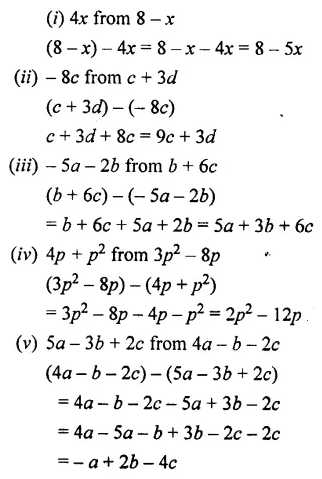
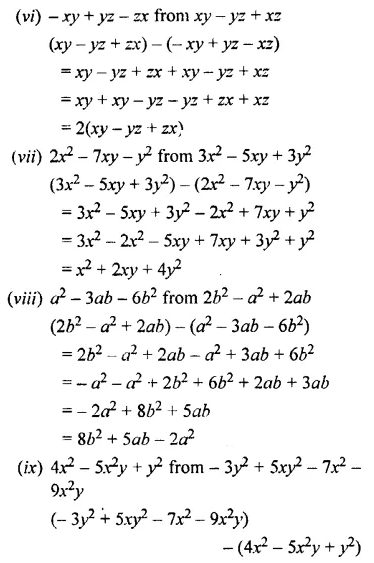
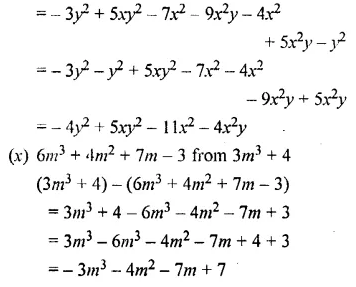
Question 11.
Subtract – 5a² – 3a + 1 from the sum of 4a² + 3 – 8a and 9a – 7.
Solution:

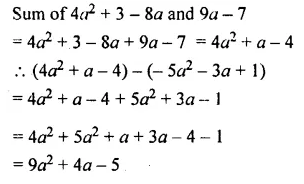
Question 12.
By how much does 8x³ – 6x² + 9x – 10 exceed 4x³ + 2x² + 7x -3 ?
Solution:

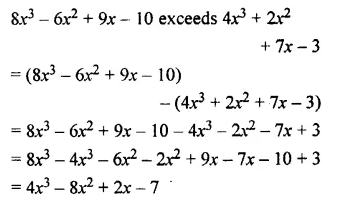
Question 13.
What must be added to 2a³ + 5a – a² – 6 to get a² – a – a³ + 1 ?
Solution:

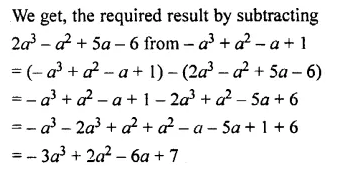
Question 14.
What must be subtracted from a² + b² + lab to get – 4ab + 2b² ?
Solution:

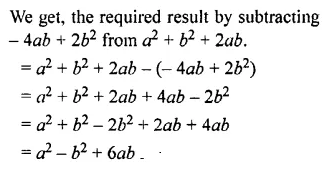
Question 15.
Find the excess of 4m² + 4n² + 4p² over m²+ 3n² – 5p²
Solution:

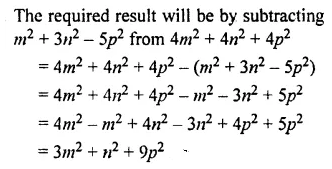
Question 16.
By how much is 3x³ – 2x²y + xy² -y³ less than 4x³ – 3x²y – 7xy² +2y³
Solution:

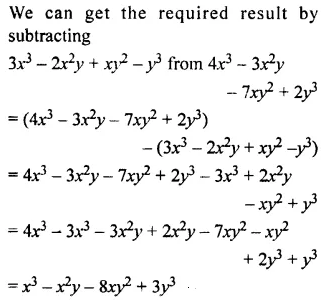
Question 17.
Subtract the sum of 3a² – 2a + 5 and a² – 5a – 7 from the sum of 5a² -9a + 3 and 2a – a² – 1
Solution:

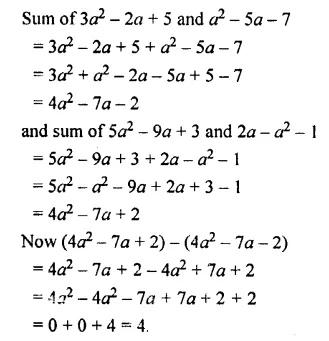
Question 18.
The perimeter of a rectangle is 28x³+ 16x² + 8x + 4. One of its sides is 8x² + 4x. Find the other side
Solution:

Question 19.
The perimeter of a triangle is 14a² + 20a + 13. Two of its sides are 3a² + 5a + 1 and a² + 10a – 6. Find its third side.
Solution:

Question 20.

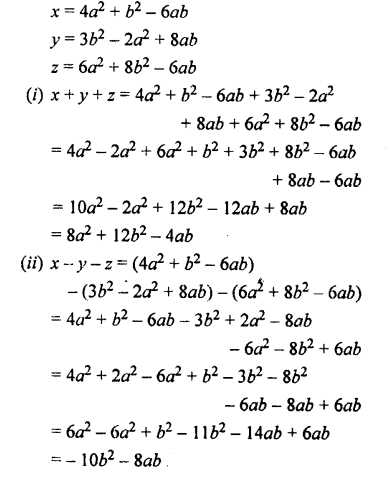
Solution:

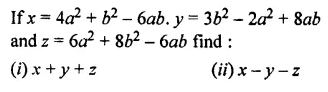
Question 21.

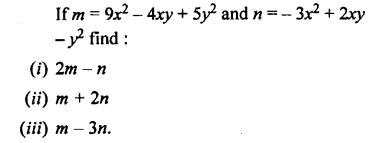
Solution:

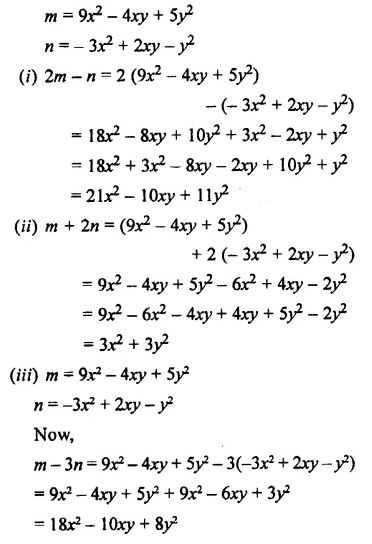
Question 22.
Simplify:

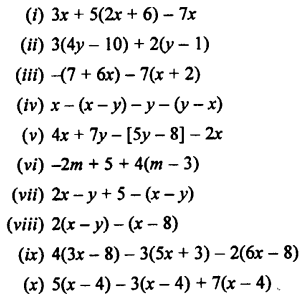
Solution:

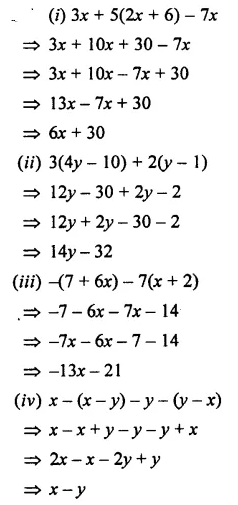
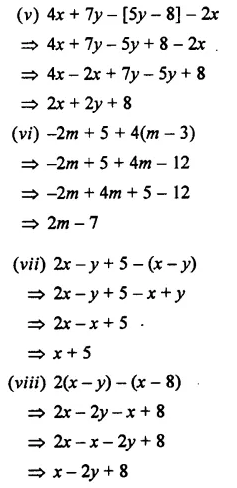
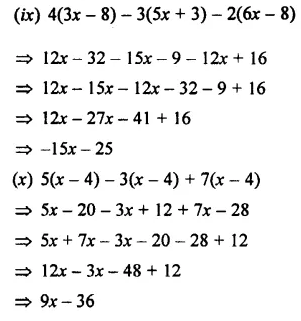
EXERCISE 11 (C)

Question 1.
Multiply:

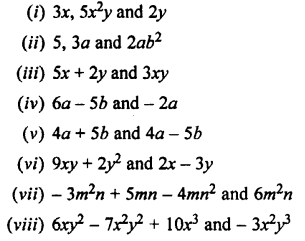
Solution:

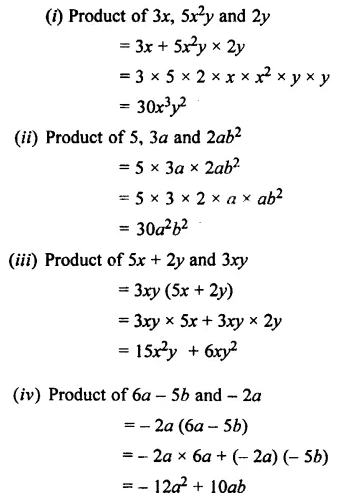
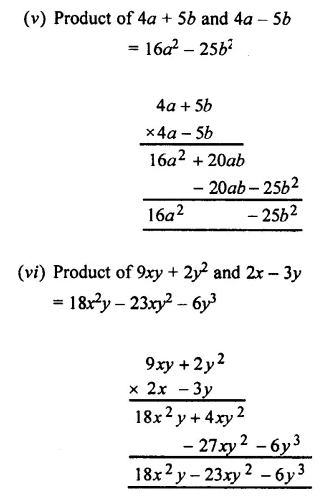
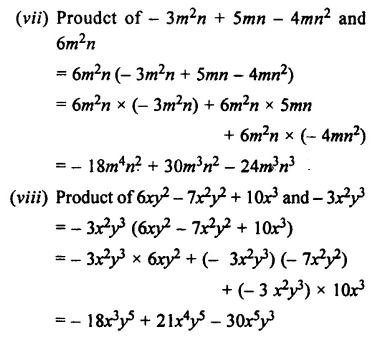
Question 2.
Copy and complete the following multi-plications :

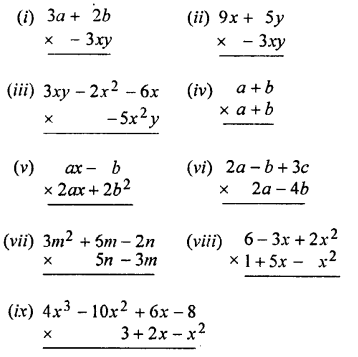
Solution:

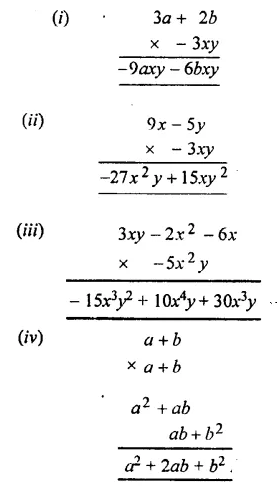
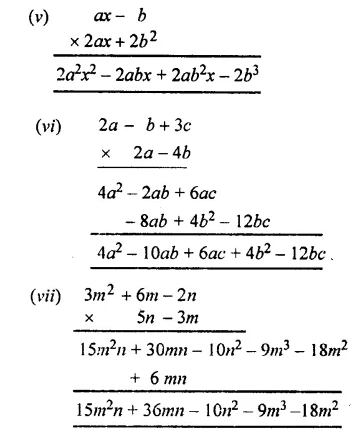
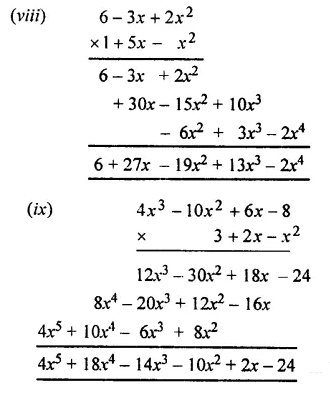
Question 3.
Evaluate :

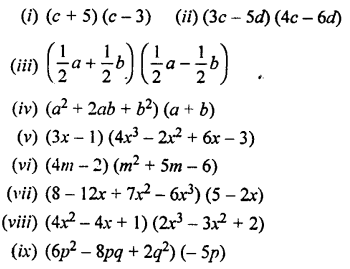
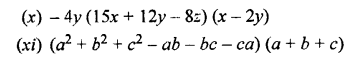
Solution:

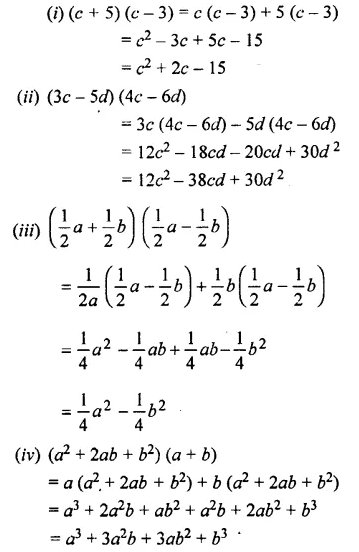
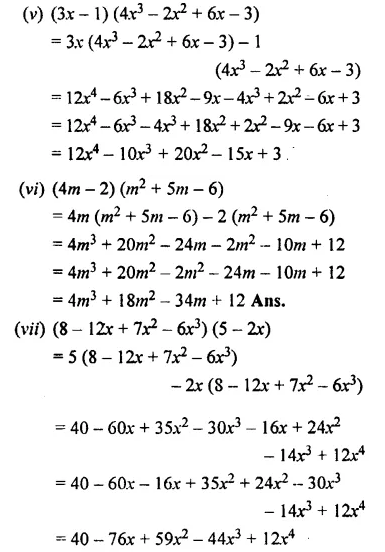
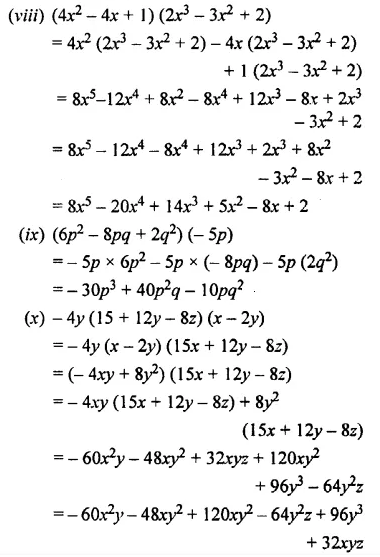
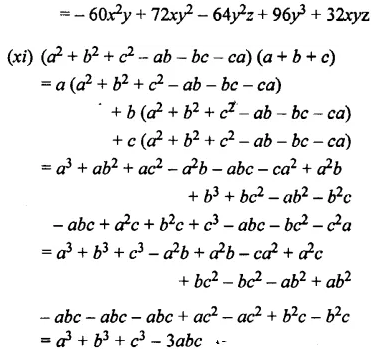
Question 4.
Evaluate:

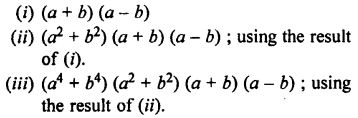
Solution:

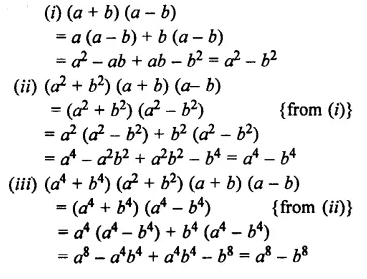
Question 5.
Evaluate :

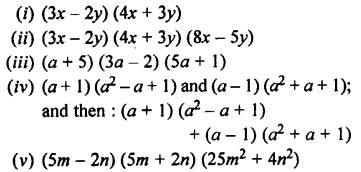
Solution:

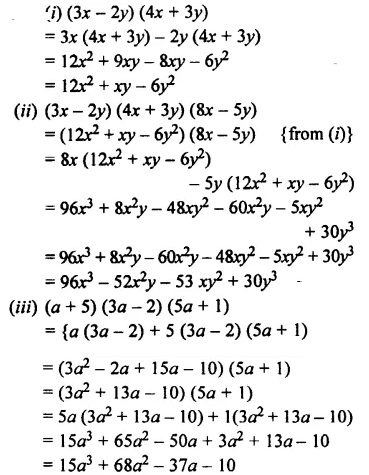
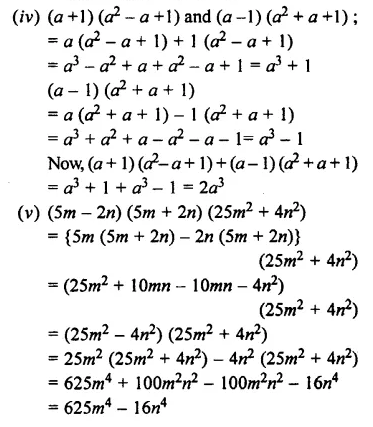
Question 6.
Multiply:

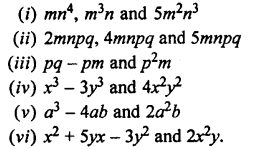
Solution:

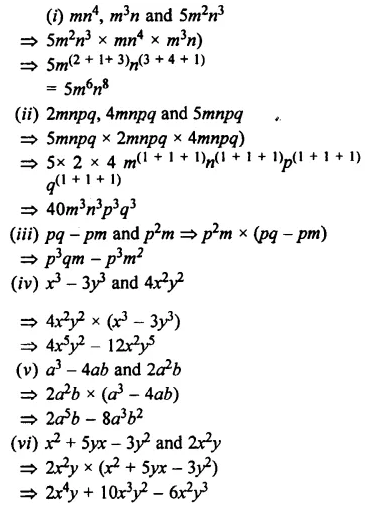
Question 7.
Multiply:

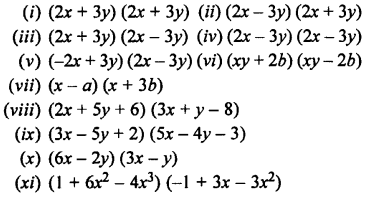
Solution:

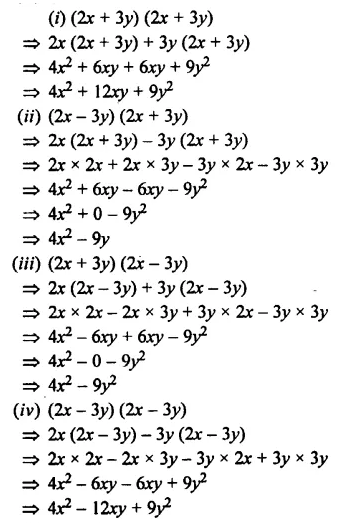
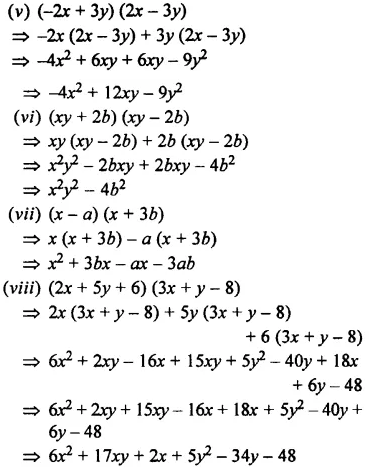
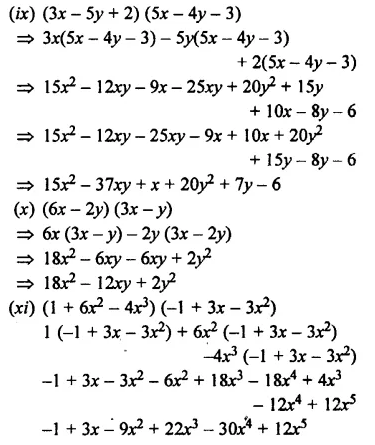
EXERCISE 11 (D)

Question 1.
Divide:

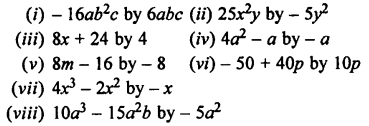
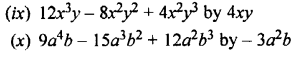
Solution:

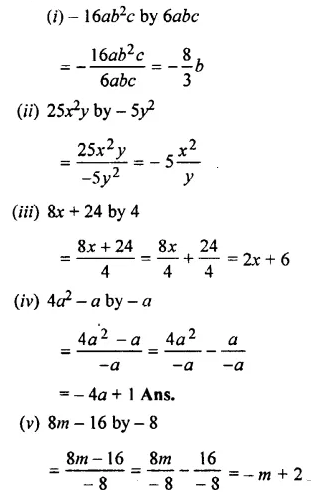
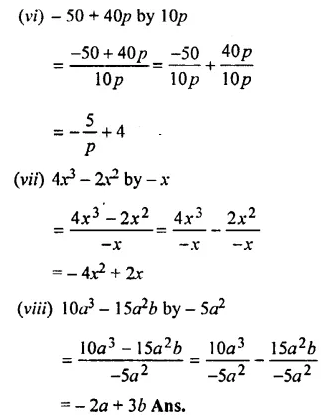
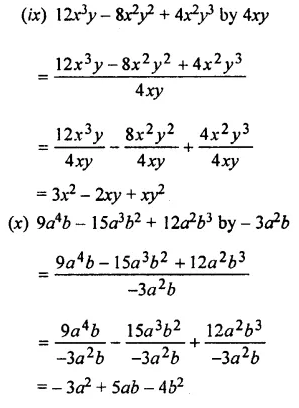
Question 2.
Divide :

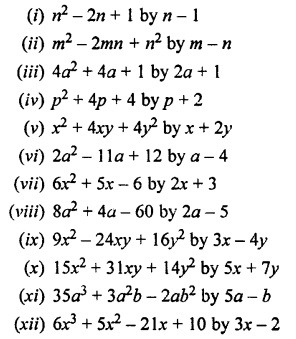
Solution:

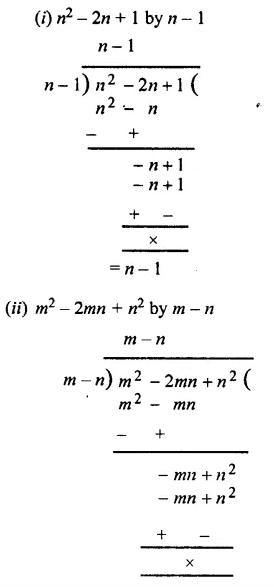
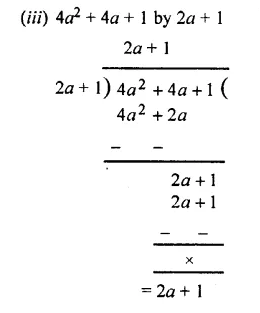
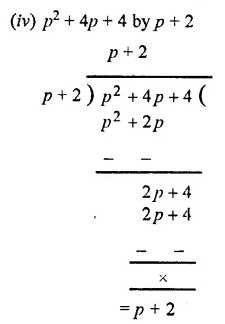
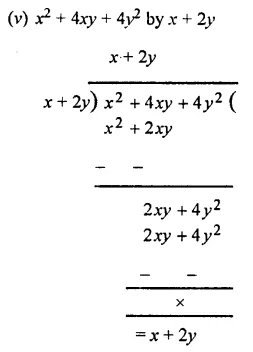
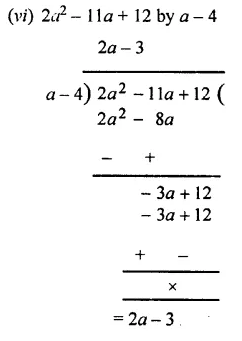
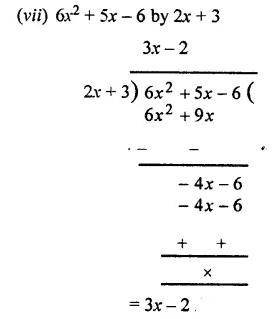
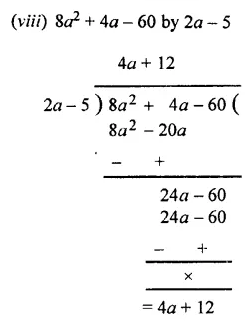
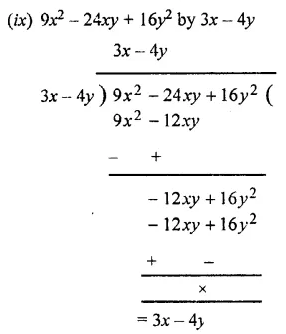
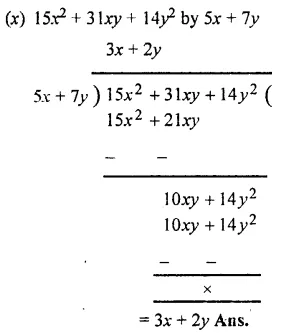
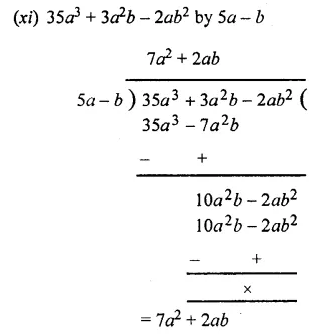
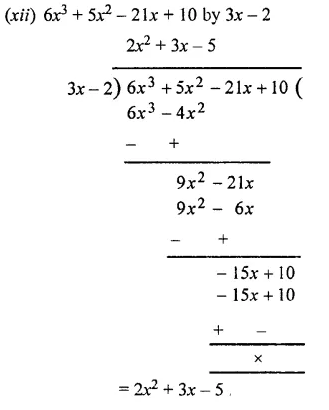
Question 3.
The area of a rectangle is 6x²– 4xy – 10y² square unit and its length is 2x + 2y unit. Find its breadth
Solution:

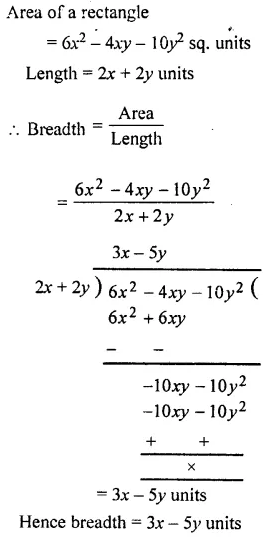
Question 4.
The area of a rectangular field is 25x² + 20xy + 3y² square unit. If its length is 5x + 3y unit, find its breadth, Hence find its perimeter.
Solution:

Question 5.
Divide:

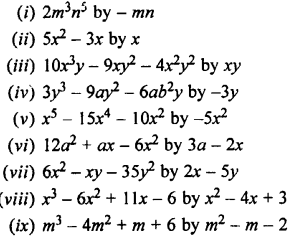
Solution:

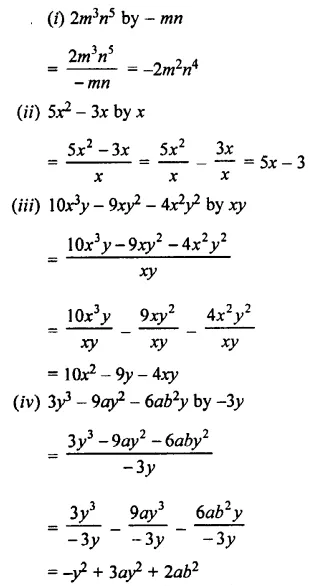
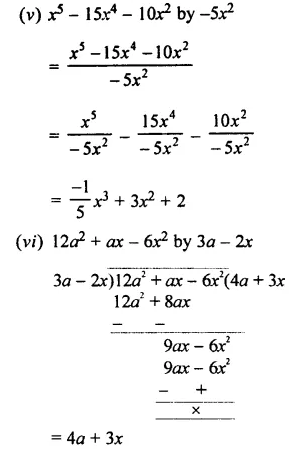
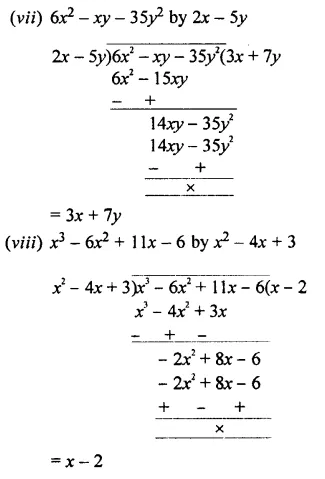
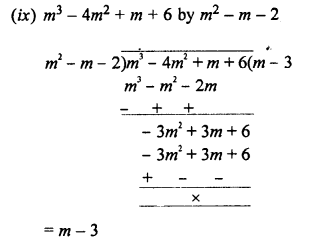
EXERCISE 11 (E)

Simplify
Question 1.

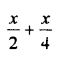
Solution:

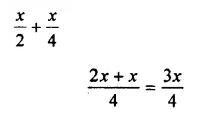
Question 2.

Solution:

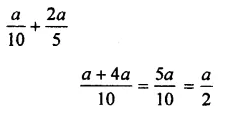
Question 3.

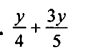
Solution:

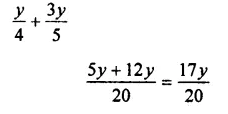
Question 4.

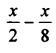
Solution:

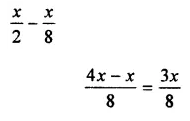
Question 5.

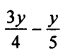
Solution:

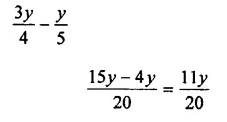
Question 6.

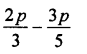
Solution:

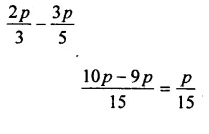
Question 7.

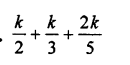
Solution:

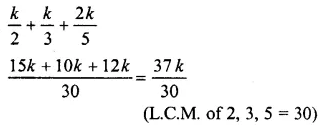
Question 8.

Solution:

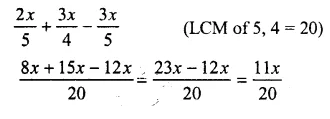
Question 9.

Solution:

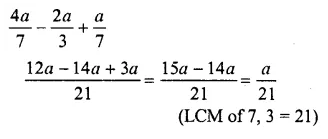
Question 10.

Solution:

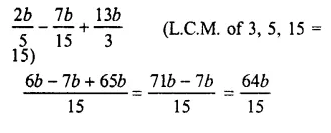
Question 11.

Solution:

Question 12.

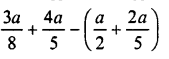
Solution:

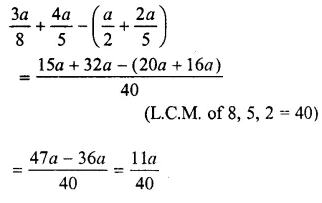
Question 13.

Solution:

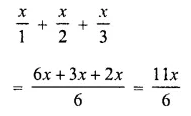
Question 14.

Solution:

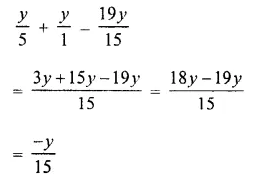
Question 15.

Solution:

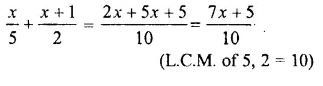
Question 16.

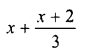
Solution:

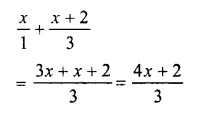
Question 17.

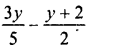
Solution:

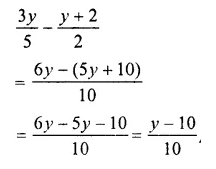
Question 18.

Solution:

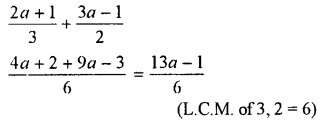
Question 19.

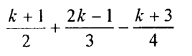
Solution:

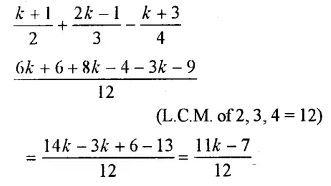
Question 20.

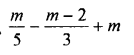
Solution:

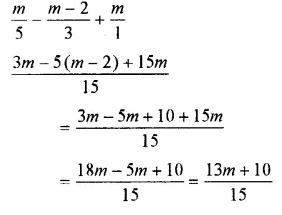
Question 21.

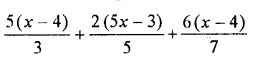
Solution:

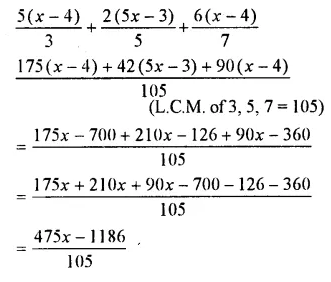
Question 22.

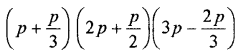
Solution:

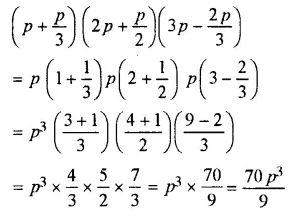
Question 23.

Solution:

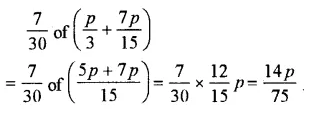
Question 24.

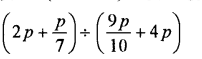
Solution:

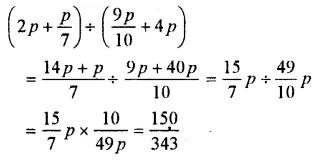
Question 25.

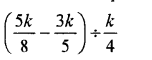
Solution:

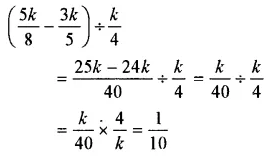
Question 26.

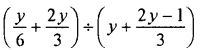
Solution:

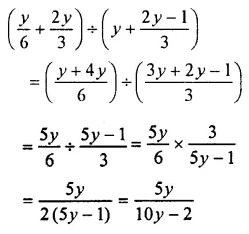
EXERCISE 11 (F)

Enclose the given terms in brackets as required :

Question 1.
 x – y – z = x-{…….)
Solution:

Question 2.
x² – xy² – 2xy – y² = x² – (…….. )
Solution:

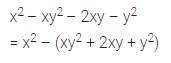
Question 3.
4a – 9 + 2b – 6 = 4a – (…….. )
Solution:

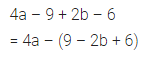
Question 4.
x² -y² + z² + 3x – 2y = x² – (…….. )
Solution:

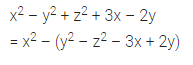
Question 5.
– 2a² + 4ab – 6a²b² + 8ab² = – 2a (……… )
Solution:

Simplify :

Question 6.
2x – (x + 2y- z)
Solution:

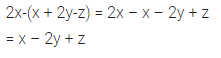
Question 7.
p + q – (p – q) + (2p – 3q)
Solution:

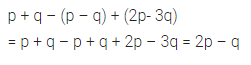
Question 8.
9x – (-4x + 5)
Solution:

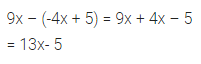
Question 9.
6a – (- 5a – 8b) + (3a + b)
Solution:

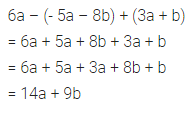
 Question 10.
(p – 2q) – (3q – r)
Solution:

Question 11.
9a (2b – 3a + 7c)
Solution:

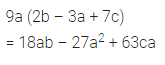
Question 12.
-5m (-2m + 3n – 7p)
Solution:

Question 13.
-2x (x + y) + x²
Solution:

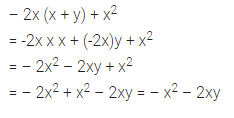
Question 14.

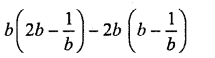
Solution:

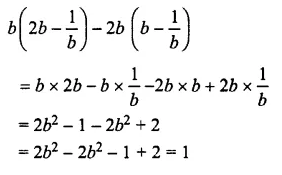
Question 15.
8 (2a + 3b – c) – 10 (a + 2b + 3c)
Solution:

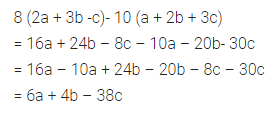
Question 16.

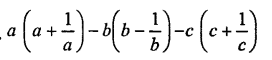
Solution:

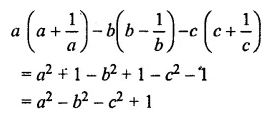
Question 17.
5 x (2x + 3y) – 2x (x – 9y)
Solution:

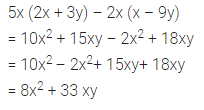
Question 18.
a + (b + c – d)
Solution:

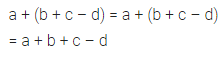
Question 19.
5 – 8x – 6 – x
Solution:

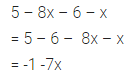
Question 20.
2a + (6- \(\overline { a-b }\) )
Solution:

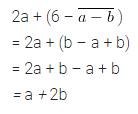
Question 21.
3x + [4x – (6x – 3)]
Solution:

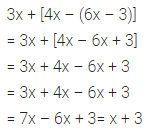
Question 22.
5b – {6a + (8 – b – a)}
Solution:

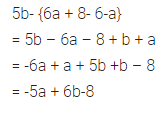
Question 23.
2x-[5y- (3x -y) + x]
Solution:

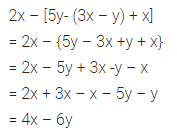
Question 24.
6a – 3 (a + b – 2)
Solution:

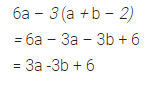
Question 25.
8 [m + 2n-p – 7 (2m -n + 3p)]
Solution:

Question 26.
{9 – (4p – 6q)} – {3q – (5p – 10)}
Solution:

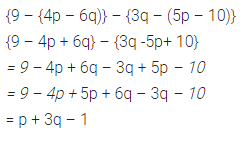
Question 27.
2 [a – 3 {a + 5 {a – 2) + 7}]
Solution:

Question 28.
5a – [6a – {9a – (10a – \(\overline { 4a-3a }\)  )}]
Solution:

Question 29.
9x + 5 – [4x – {3x – 2 (4x – 3)}]
Solution:

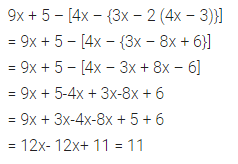
Question 30.
(x + y – z)x + (z + x – y)y – (x + y – z)z
Solution:

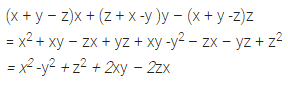
Question 31.
-1 [a-3 {b -4 (a-b-8) + 4a} + 10]
Solution:

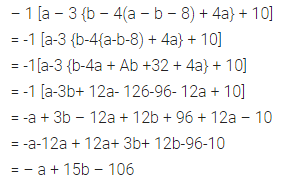
Question 32.

Solution:

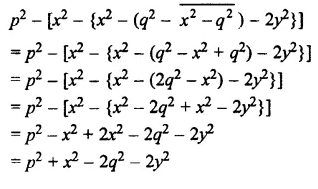
Question 33.
10 – {4a – (7 – \(\overline { a-5 }\)) – (5a – \(\overline { 1+a }\))}
Solution:

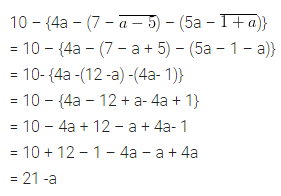
Question 34.
7a- [8a- (11a-(12a- \(\overline { 6a-5a }\))}]
Solution:

Question 35.

Solution:

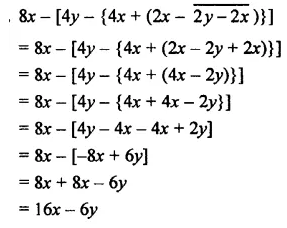
Question 36.
x-(3y- \(\overline { 4z-3x }\) +2z- \(\overline { 5y-7x }\))
Solution:

Selina Concise Mathematics Class 7 ICSE Solutions