Selina Concise Mathematics Class 7 ICSE Solutions Chapter 16 Pythagoras Theorem
Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 16 Pythagoras Theorem
Pythagoras Theorem Exercise 16 – Selina Concise Mathematics Class 7 ICSE Solutions
Question 1.
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
Solution:
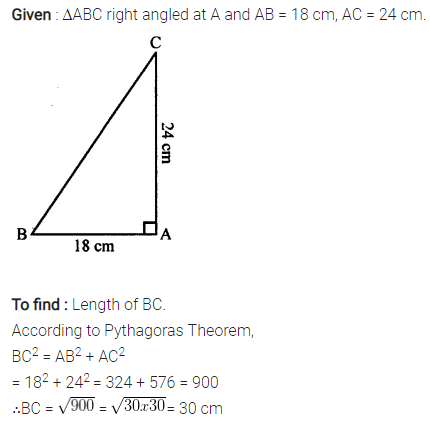
Question 2.
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
Solution:

Question 3.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if:
PQ = 34 cm and QR = 33.6 cm.
Solution:
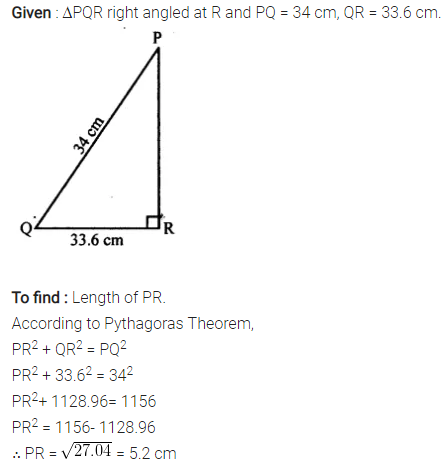
Question 4.
The sides of a certain triangle are given below. Find, which of them is right-triangle
(i) 16 cm, 20 cm and 12 cm
(ii) 6 m, 9 m and 13 m
Solution:

Question 5.
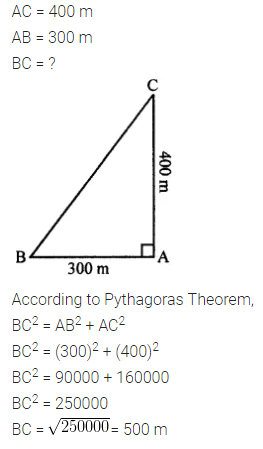
In the given figure, angle BAC = 90°, AC = 400 m and AB = 300 m. Find the length of BC.
Solution:
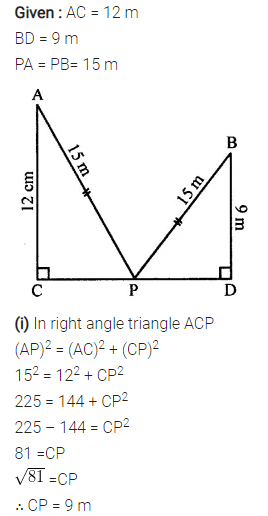
Question 6.
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD
Solution:

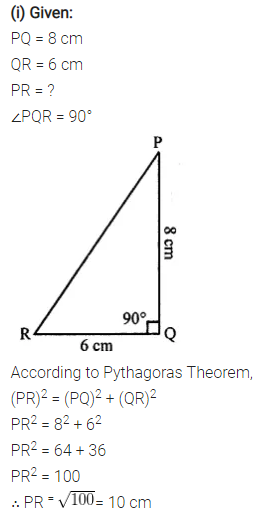
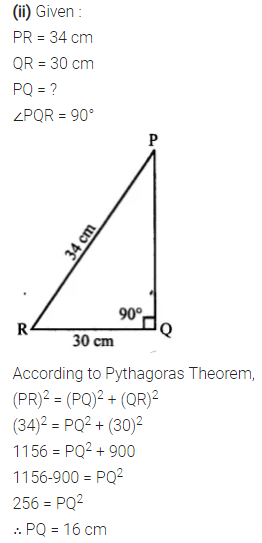
Question 7.
In triangle PQR, angle Q = 90°, find :
(i) PR, if PQ = 8 cm and QR = 6 cm
(ii) PQ, if PR = 34 cm and QR = 30 cm
Solution:
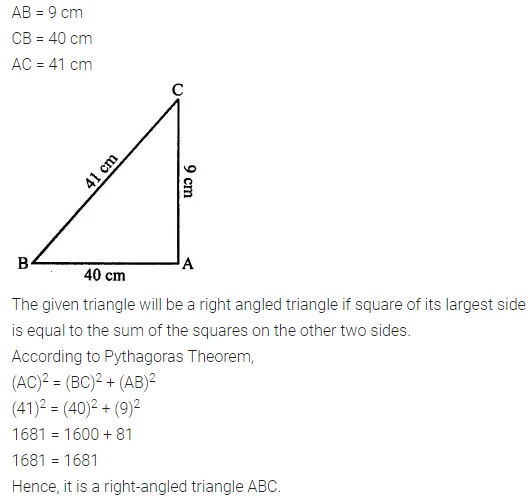
Question 8.
Show that the triangle ABC is a right-angled triangle; if:
AB = 9 cm, BC = 40 cm and AC = 41 cm
Solution:
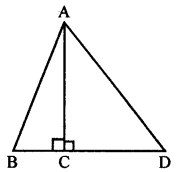
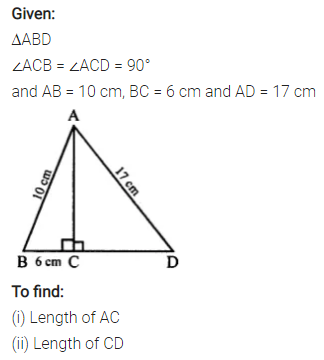
Question 9.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD
Solution:

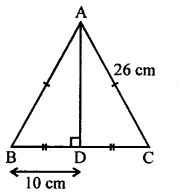
Question 10.
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.
Solution:

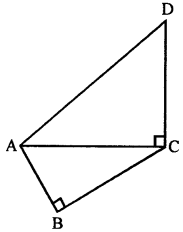
Question 11.
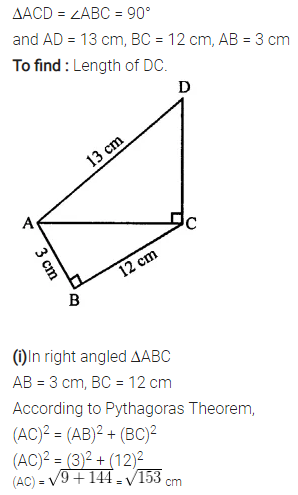
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.
Solution:

Question 12.
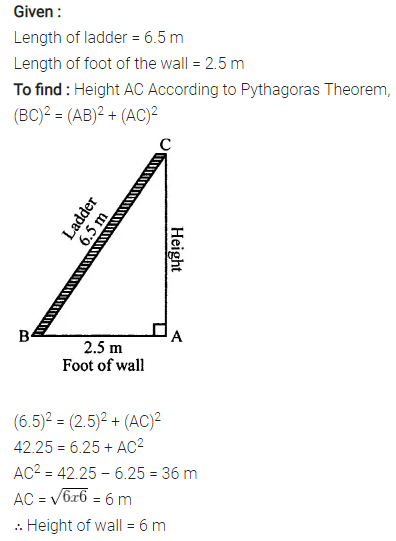
A ladder, 6.5 m long, rests against a vertical wall. Ifthe foot of the ladcler is 2.5 m from the foot of the wall, find upto how much height does the ladder reach?
Solution:
Question 13.
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
Solution:

Question 14.
Use the information given in the figure to find the length AD.
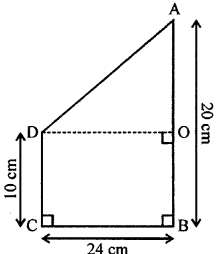
Solution:
