Selina Concise Mathematics Class 8 ICSE Solutions Chapter 21 Surface Area, Volume and Capacity (Cuboid, Cube and Cylinder)
Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 21 Surface Area, Volume and Capacity (Cuboid, Cube and Cylinder)
Surface Area, Volume and Capacity Exercise 21A – Selina Concise Mathematics Class 8 ICSE Solutions
Question 1.
Find the volume and the total surface area of a cuboid, whose :
(i) length = 15 cm, breadth = 10 cm and height = 8 cm.
(ii) l = 3.5 m, b = 2.6 m and h = 90 cm,
Solution:

Question 2.
(i) The volume of a cuboid is 3456 cm3. If its length = 24 cm and breadth = 18 cm ; find its height.
(ii) The volume of a cuboid is 7.68 m3. If its length = 3.2 m and height = 1.0 m; find its breadth.
(iii) The breadth and height of a rectangular solid are 1.20 m and 80 cm respectively. If the volume of the cuboid is 1.92 m3; find its length.
Solution:


Question 3.
The length, breadth and height of a cuboid are in the ratio 5 : 3 : 2. If its volume is 240 cm3; find its dimensions. (Dimensions means : its length, breadth and height). Also find the total surface area of the cuboid.
Solution:

Question 4.
The length, breadth and height of a cuboid are in the ratio 6 : 5 : 3. If its total surface area is 504 cm2; find its dimensions. Also, find the volume of the cuboid.
Solution:

Question 5.
Find the volume and total surface area of a cube whose each edge is :
(i) 8 cm
(ii) 2 m 40 cm.
Solution:
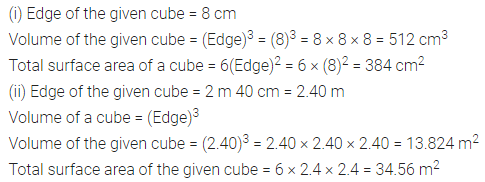
Question 6.
Find the length of each edge of a cube, if its volume is :
(i) 216 cm3
(ii) 1.728 m3
Solution:

Question 7.
The total surface area of a cube is 216 cm2. Find its volume.
Solution:
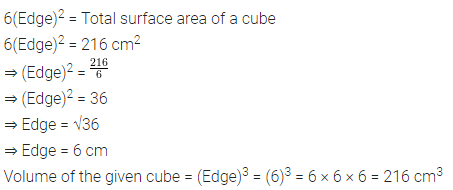
Question 8.
A solid cuboid of metal has dimensions 24 cm, 18 cm and 4 cm. Find its volume.
Solution:
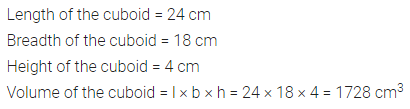
Question 9.
A wall 9 m long, 6 m high and 20 cm thick, is to be constructed using bricks of dimensions 30 cm, 15 cm and 10 cm. How many bricks will be required.
Solution:

Question 10.
A solid cube of edge 14 cm is melted down and recasted into smaller and equal cubes each of edge 2 cm; find the number of smaller cubes obtained.
Solution:
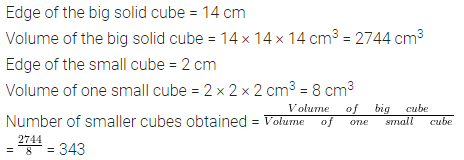
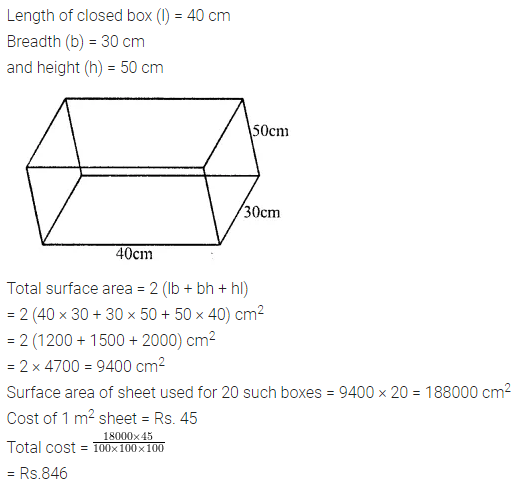
Question 11.
A closed box is cuboid in shape with length = 40 cm, breadth = 30 cm and height = 50 cm. It is made of thin metal sheet. Find the cost of metal sheet required to make 20 such boxes, if 1 m2 of metal sheet costs Rs. 45.
Solution:
Question 12.
Four cubes, each of edge 9 cm, are joined as shown below :
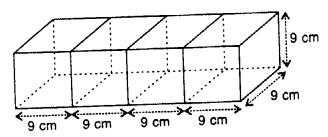
Write the dimensions of the resulting cuboid obtained. Also, find the total surface area and the volume of the resulting cuboid.
Solution:
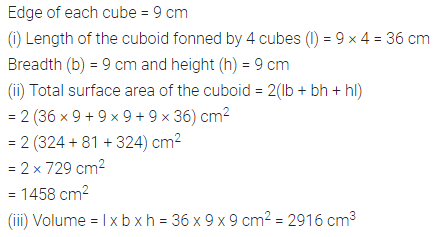
Surface Area, Volume and Capacity Exercise 21B – Selina Concise Mathematics Class 8 ICSE Solutions
Question 1.
How many persons can be accommodated in a big-hall of dimensions 40 m, 25 m and 15 m ; assuming that each person requires 5 m3 of air?
Solution:

Question 2.
The dimension of a class-room are; length = 15 m, breadth = 12 m and height = 7.5 m. Find, how many children can be accommodated in this class-room ; assuming 3.6 m3 of air is needed for each child.
Solution:

Question 3.
The length, breadth and height of a room are 6 m, 5.4 m and 4 m respectively. Find the area of :
(i) its four-walls
(ii) its roof.
Solution:
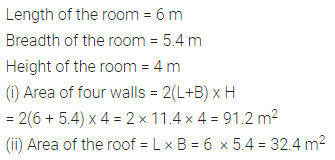
Question 4.
A room 5 m long, 4.5 m wide and 3.6 m high has one door 1.5 m by 2.4 m and two windows, each 1 m by 0.75 m. Find :
(i) the area of its walls, excluding door and windows ;
(ii) the cost of distempering its walls at the rate of Rs.4.50 per m2.
(iii) the cost of painting its roof at the rate of Rs.9 per m2.
Solution:


Question 5.
The dining-hall of a hotel is 75 m long ; 60 m broad and 16 m high. It has five – doors 4 m by 3 m each and four windows 3 m by 1.6 m each. Find the cost of :
(i) papering its walls at the rate of Rs.12 per m2;
(ii) carpetting its floor at the rate of Rs.25 per m2.
Solution:

Question 6.
Find the volume of wood required to make a closed box of external dimensions 80 cm, 75 cm and 60 cm, the thickness of walls of the box being 2 cm throughout.
Solution:

Question 7.
A closed box measures 66 cm, 36 cm and 21 cm from outside. If its walls are made of metal-sheet, 0.5 cm thick ; find :
(i) the capacity of the box ;
(ii) volume of metal-sheet and
(iii) weight of the box, if 1 cm3 of metal weights 3.6 gm.
Solution:

Question 8.
The internal length, breadth and height of a closed box are 1 m, 80 cm and 25 cm. respectively. If its sides are made of 2.5 cm thick wood ; find :
(i) the capacity of the box
(ii) the volume of wood used to make the box.
Solution:

Question 9.
Find the area of metal-sheet required to make an open tank of length = 10 m, breadth = 7.5 m and depth = 3.8 m.
Solution:

Question 10.
A tank 30 m long, 24 m wide and 4.5 m deep is to be made. It is open from the top. Find the cost of iron-sheet required, at the rate of ₹ 65 per m2, to make the tank.
Solution:

Surface Area, Volume and Capacity Exercise 21C – Selina Concise Mathematics Class 8 ICSE Solutions
Question 1.
The edges of three solid cubes are 6 cm, 8 cm and 10 cm. These cubes are melted and recast into a single cube. Find the edge of the resulting cube.
Solution:

Question 2.
Three solid cubes of edges 6 cm, 10 cm and x cm are melted to form a single cube of edge 12 cm, find the value of x.
Solution:

Question 3.
The length of the diagonals of a cube is 8√3 cm.
Find its:
(i) edge
(ii) total surface area
(iii) Volume
Solution:
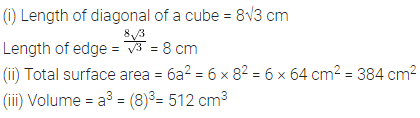
Question 4.
A cube of edge 6 cm and a cuboid with dimensions 4 cm x x cm x 15 cm are equal in volume. Find:
(i) the value of x.
(ii) total surface area of the cuboid.
(iii) total surface area of the cube.
(iv) which of these two has greater surface and by how much?
Solution:

Question 5.
The capacity of a rectangular tank is 5.2 m3 and the area of its base is 2.6 x 104 cm2; find its height (depth).
Solution:
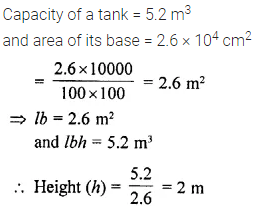
Question 6.
The height of a rectangular solid is 5 times its width and its length is 8 times its height. If the volume of the wall is 102.4 cm3, find its length.
Solution:

Question 7.
The ratio between the lengths of the edges of two cubes are in the ratio 3 : 2. Find the ratio between their:
(i) total surface area
(ii) volume.
Solution:
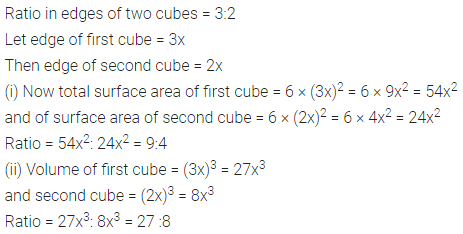
Question 8.
The length, breadth and height of a cuboid (rectangular solid) are 4 : 3 : 2.
(i) If its surface are is 2548 cm2, find its volume.
(ii) If its volume is 3000 m3, find its surface area.
Solution:

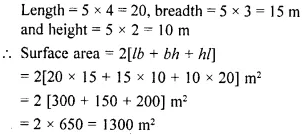
Surface Area, Volume and Capacity Exercise 21D – Selina Concise Mathematics Class 8 ICSE Solutions
Question 1.
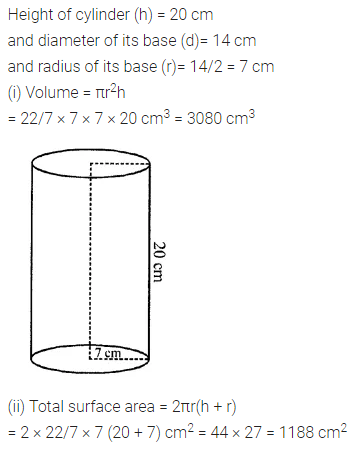
The height of a circular cylinder is 20 cm and the diameter of its base is 14 cm. Find:
(i) the volume
(ii) the total surface area.
Solution:
Question 2.
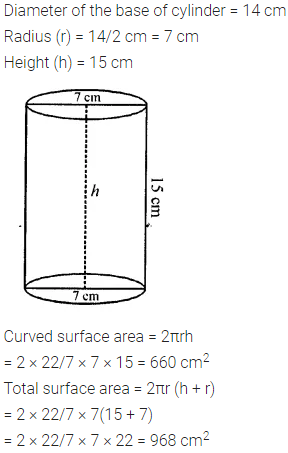
Find the curved surface area and the total surface area of a right circular cylinder whose height is 15 cm and the diameter of the cross-section is 14 cm.
Solution:
Question 3.
Find the height of the cylinder whose radius is 7 cm and the total surface area is 1100 cm2.
Solution:

Question 4.
The curved surface area of a cylinder of height 14 cm is 88 cm2. Find the diameter of the base of the cylinder.
Solution:

Question 5.
The ratio between the curved surface area and the total surface area of a cylinder is 1 : 2. Find the ratio between the height and the radius of the cylinder.
Solution:

Question 6.
Find the capacity of a cylindrical container with internal diameter 28 cm and height 20 cm.
Solution:

Question 7.
The total surface area of a cylinder is 6512 cm2 and the circumference of its bases is 88 cm. Find:
(i) its radius
(ii) its volume
Solution:

Question 8.
The sum of the radius and the height of a cylinder is 37 cm and the total surface area of the cylinder is 1628 cm2. Find the height and the volume of the cylinder.
Solution:

Question 9.
A cylindrical pillar has radius 21 cm and height 4 m. Find :
(i) the curved surface area of the pillar
(ii) cost of polishing 36 such cylindrical pillars at the rate of ₹ 12 per m2.
Solution:

Question 10.
If radii of two cylinders are in the ratio 4 : 3 and their heights are in the ratio 5 : 6, find the ratio of their curved surfaces.
Solution:

Surface Area, Volume and Capacity Exercise 21E – Selina Concise Mathematics Class 8 ICSE Solutions
Question 1.
A cuboid is 8 m long, 12 m broad and 3.5 high, Find its
(i) total surface area
(ii) lateral surface area
Solution:

Question 2.
How many bricks will be required for constructing a wall which is 16 m long, 3 m high and 22.5 cm thick, if each brick measures 25 cm x 11.25 cm x 6 cm?
Solution:

Question 3.
The length, breadth and height of cuboid are in the ratio 6 : 5 : 3. If its total surface area is 504 cm2, find its volume.
Solution:

Question 4.
The external dimensions of an open wooden box are 65 cm, 34 cm and 25 cm. If the box is made up of wood 2 cm thick, find the capacity of the box and the volume of wood used to make it.
Solution:

Question 5.
The curved surface area and the volume of a toy, cylindrical in shape, are 132 cm2 and 462 cm3 respectively. Find, its diameter and its length.
Solution:
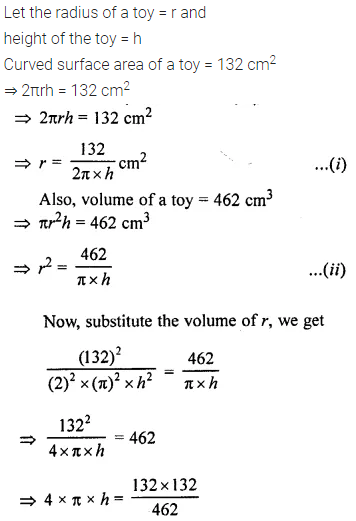
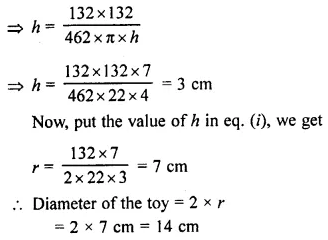
Question 6.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹ 10 per m2 is ₹ 15,000, find the height of the hall.
Solution:
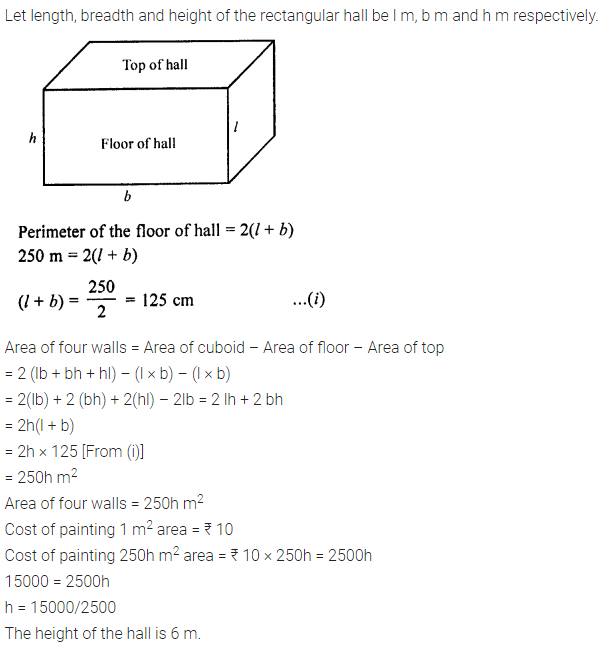
Question 7.
The length of a hall is double its breadth. Its height is 3 m. The area of its four walls (including doors and windows) is 108 m2, find its volume.
Solution:
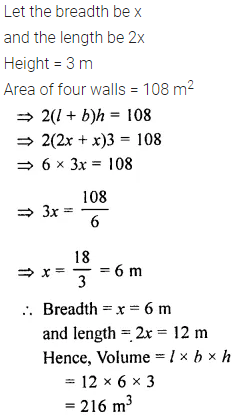
Question 8.
A solid cube of side 12 cm is cut into 8 identical cubes. What will be the side of the new cube? Also, find the ratio between the surface area of the original cube and the total surface area of all the small cubes formed.
Solution:
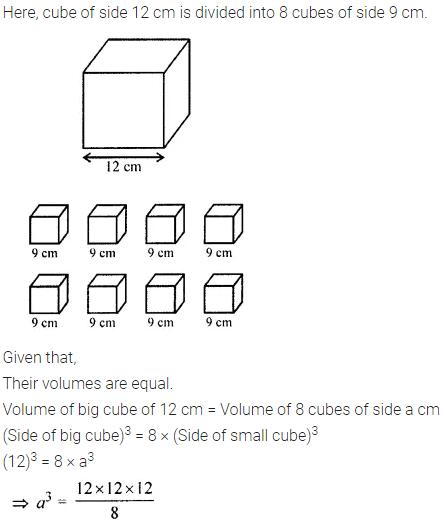

Question 9.
The diameter of a garden roller is 1.4 m and it 2 m long. Find the maximum area covered by it 50 revolutions?
Solution:

Question 10.
In a building, there are 24 cylindrical pillars. For each pillar, radius is 28 m and height is 4 m. Find the total cost of painting the curved surface area of the pillars at the rate of ₹ 8 per m2.
Solution:
