Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.
Stability of Metal Complexes
The stability of coordination complexes can be interpreted in two different ways. The first one is thermodynamic stability and second one is kinetic stability. Thermodynamic stability of a coordination complex refers to the free energy change (∆G) of a complex formation reaction. Kinetic stability of a coordination complex refers to the ligand substitution. In some cases, complexes can undergo rapid ligand substitution; such complexes are called labile complexes. However, some complexes undergo ligand substitution very slowly (or sometimes no substitution), such complexes are called inert complexes.
Stability Constant: (β)
The stability of a coordination complex is a measure of its resistance to the replacement of one ligand by another. The stability of a complex refers to the degree of association between two species involved in an equilibrium. Let us consider the following complex formation reaction
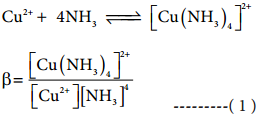
So, as the concentration of [Cu(NH3)4]2+ increases the value of stability complexes also increases. Therefore the greater the value of stability constant greater is the stability of the complex.
Generally coordination complexes are stable in their solutions; however, the complex ion can undergo dissociation to a small extent. Extent of dissociation depends on the strength of the metal ligand bond, thus Stronger the M ← L, lesser is the dissociation.
In aqueous solutions, when complex ion dissociates, there will be equilibrium between undissociated complex ion and dissociated ions. Hence the stability of the metal complex can be expressed in terms of dissociation equilibrium constant or instability constant (α). For example let us consider the dissociation of [Cu(NH3)4]2+ in aqueous solution.
[Cu(NH3)4]2+ ⇄ Cu2+ + 4NH3
The dissociation equilibrium constant or instability constant is represented as follows,
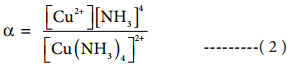
From (1) and (2) we can say that, the reciprocal of dissociation equilibrium constant (α) is called as formation equilibrium constant or stability constant (β). β = (\(\frac{1}{α}\)).
Significance of Stability Constants
The stability of coordination complex is measured in terms of its stability constant (β). Higher the value of stability constant for a complex ion, greater is the stability of the complex ion. Stability constant values of some important complexes are listed in table
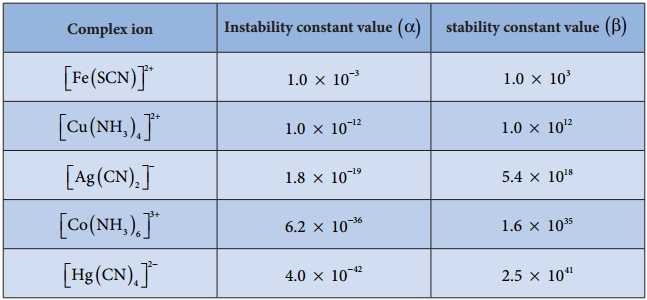
By comparing stability constant values in the above table, we can say that among the five complexes listed, [Hg(CN)4]2- is most stable complex ion and [Fe(SCN)]2+ is least stable.
Stepwise Formation Constants and Overall Formation Constants
When a free metal ion is in aqueous medium, it is surrounded by (coordinated with) water molecules. It is represented as [MS6]. If ligands which are stronger than water are added to this metal salt solution, coordinated water molecules are replaced by strong ligands.
Let us consider the formation of a metal complex ML6 in aqueous medium. (Charge on the metal ion is ignored) complex formation may occur in single step or step by step. If ligands added to the metal ion in single step, then
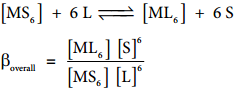
βoverall is called as overall stability constant. As solvent is present in large excess, its concentration in the above equation can be ignored.
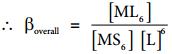
If these six ligands are added to the metal ion one by one, then the formation of complex [ML6] can be supposed to take place through six different steps as shown below. Generally step wise stability constants are represented by the symbol k.
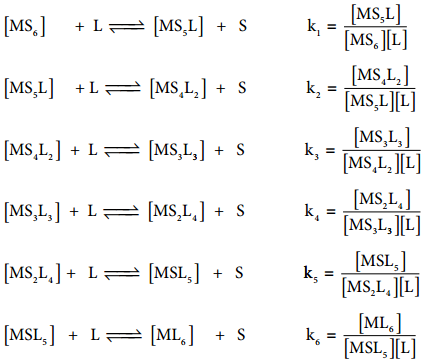
In the above equilibrium, the values k1, k2, k3, k4, k5 and k6 are called step wise stability constants. By carrying out small a mathematical manipulation, we can show that overall stability constant β is the product of all step wise stability constants k1, k2, k3, k4, k5 and k6.
β = k1 × k2 × k3 × k4 × k5 × k6
On taking logarithm both sides
log(β) = log(k1) + log(k2) + log(k3) + log(k4) + log(k5) + log(k6).