Force on A Current Carrying Conductor In A Magnetic Field
French scientist Andre Marie Ampere (1775-1836) suggested that the magnet must also exert an equal and opposite force on the current-carrying conductor. The force due to a magnetic field acting on a current-carrying conductor can be demonstrated through the following activity.
Example 1.
Case-Based:
Take a small aluminium rod AB of about 5 cm. Using two connecting wires suspend it horizontally from a stand, as shown in Fig. below.
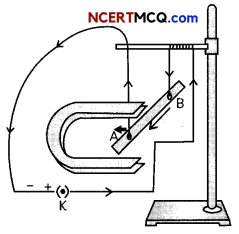
Place a strong horseshoe magnet in such a way that the rod lies between the two poles with the magnetic field directed upwards. Connect the aluminium rod in series with a battery, a key and a rheostat. Now pass a current through the aluminium rod from end B to end A. Reverse the direction of current flowing through the rod and observe the direction of its displacement.
(A) Select the correct statements based on the observations on passing current through the aluminium rod:
(I) The rod gets displaced towards the left when current is passed through the aluminium rod from end B to A.
(II) The rod gets displaced towards the right when current is passed through the aluminium rod from end B to A.
(III) The rod gets displaced towards the left when current is passed through the aluminium rod from end A to B.
(IV) The rod gets displaced towards the right when current is passed through the aluminium rod from end A to B.
(a) Both (I) and (III)
(b) Both (II) and (III)
(c) Both (I) and (IV)
(d) Both (II) and (IV)
Answer:
(c) Both (I) and (IV)
Explanation: The rod gets displaced towards the left when current is passed through the aluminium rod from end B to A and towards the right when current is passed through the aluminium rod from end A to B. The direction of force gets reversed when the direction of current through the conductor is reversed. The rule governing the direction of force experienced by a current-carrying conductor placed in a magnetic field is Fleming’s left-hand rule.
![]()
(B) A positively charged particle (alpha-particle) projected towards west is deflected towards the north by a magnetic field. The direction of the magnetic field is:
(a) towards south
(b) towards east
(c) downward
(d) upward
Answer:
(d) upward
Explanation: The direction of current is towards west as the positively charged particle (alpha- particle) is moving towards west. The direction of force is towards north as the particle is deflected by the magnetic field towards the north. Therefore, we can find the direction of magnetic field by applying Fleming’s left hand rule and observe that magnetic field is acting in upward direction.
(C) How should the poles of the horse shoe magnet be placed for getting a magnetic field directed vertically upwards?
Answer:
The direction of magnetic field is from the north pole of a magnet towards the south pole of the magnet. Therefore, in order to get a mag-netic field directed vertically upwards, the North pole of the magnet is put vertically below and south pole vertically above the aluminium rod.
(D) When will the magnitude of the force on the aluminium rod be largest?
Answer:
The magnitude of the force on the aluminium rod is the highest when the direction of current is at right angles to the direction of the magnetic field.
(E) Assertion (A): The direction of displacement of rod gets reversed on reversing the direction of current flowing through the rod.
Reason (R): The direction of force acting on the current-carrying rod gets reversed on inter-changing the two poles of the magnet.
(a) Both (A) and (R) are true and (R) is the cor-rect explanation of the assertion..
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the assertion..
(c) (A) is true, but (R) is false.
(d) (A) is false, but (R) is true.
Answer:
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the assertion.
Explanation: The direction of displacement of rod gets reversed on reversing the direction of current flowing through the rod as the direction of force acting on the current-carrying conductor gets reversed on reversing the direction of current through the rod. Direction of force acting on a current-carrying conductor placed in a magnetic field is given by Fleming’s left hand rule. It is also true that direction of force gets reversed on interchanging the poles of the magnet, but that does not explain the given assertion.
![]()
Example 2.
Imagine that you are sitting in a chamber with your back to one wall. An electron beam, moving horizontally from back wall towards the front wall, is deflected by a strong magnetic field to your right side. What is the direction of magnetic field?
Answer:
The direction of magnetic field is found by applying Fleming’s Left-hand rule and is found to be in downward direction.
If a current, I, is flowing along a wire of length, L, which is placed perpendicular to the direction of the magnetic field, B, then the force, F, experienced by the wire is given by, F = B I L
Or, B = \(\frac{F}{IL}\)
The direction of force is reversed when the dir-ection of current is reversed. The direction of force depends upon the direction of current and direction of magnetic field. The displacement is largest when the direction of current is at right angles to the direction of the magnetic field.
Using the fact that current is the rate of flow of charge, i.e., I = q/t, we can write, F = BqL/t or, F = B q v, where v is the velocity of the charged particle.
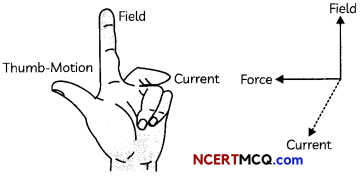
Fleming’s Left-Hand Rule
When a current-carrying conductor is placed in a magnetic field, it experiences a force, whose direction is given by Fleming’s Left Hand Rule, which states that “ Stretch the forefinger, the central finger and the thumb of your left hand mutually perpendicular to each other. If the forefinger shows the direction of the field and the central finger that of the current, then the thumb will point towards the direction of motion of the conductor, i.e.. force.