Tag: ML Aggarwal Maths for Class 10 ICSE Solutions Pdf Download

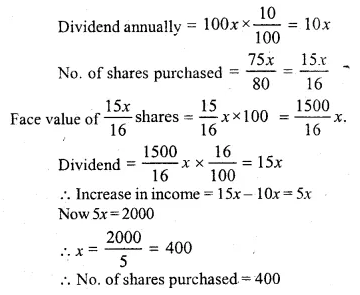
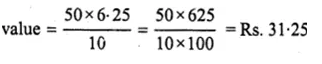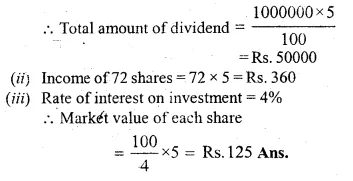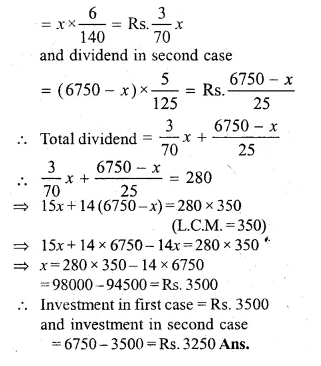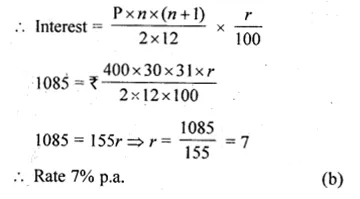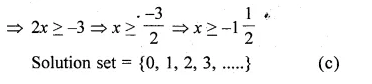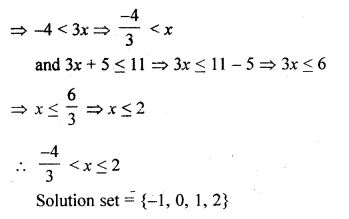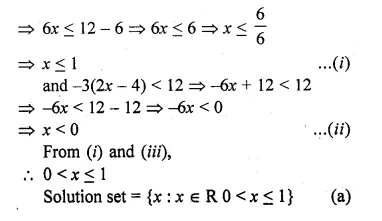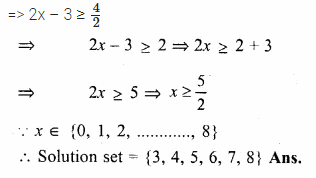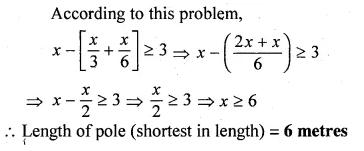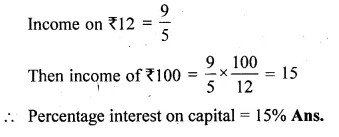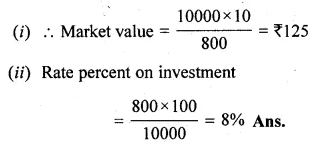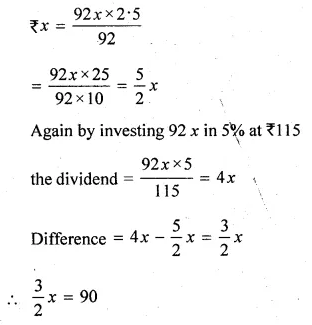ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Solve the following equations (1 to 4) by factorisation :

Question 1.
(i) x² + 6x – 16 = 0
(ii) 3x² + 11x + 10 = 0
Solution:
x² + 6x – 16 = 0
⇒ x² + 8x – 2x – 16 = 0
⇒ x (x + 8) – 2 (x + 8) = 0

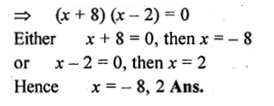
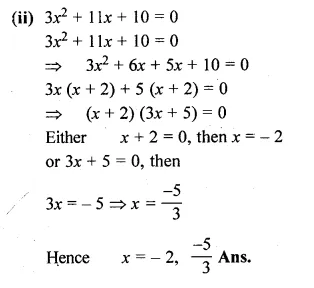
Question 2.
(i) 2x² + ax – a² = 0
(ii) √3x² + 10x + 7√3 = 0
Solution:
(i) 2x² + ax – a² = 0
⇒ 2x² + 2ax – ax – a² = 0

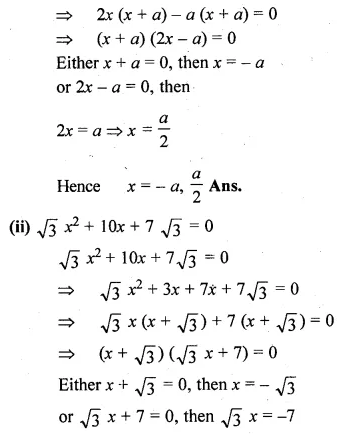
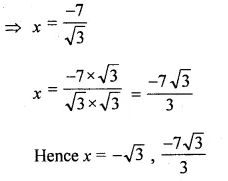
Question 3.
(i) x(x + 1) + (x + 2)(x + 3) = 42
(ii) \(\frac { 6 }{ x } -\frac { 2 }{ x-1 } =\frac { 1 }{ x-2 } \)
Solution:
(i) x(x + 1) + (x + 2)(x + 3) = 42
⇒ 2x² + 6x + 6 – 42 = 0

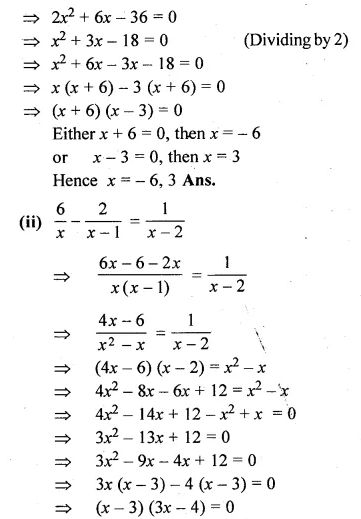
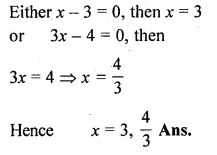
Question 4.
(i)\(\sqrt { x+15 } =x+3 \)
(ii)\(\sqrt { { 3x }^{ 2 }-2x-1 } =2x-2\)
Solution:
(i) \(\sqrt { x+15 } =x+3 \)
Squaring on both sides
x + 15 = (x + 3)²

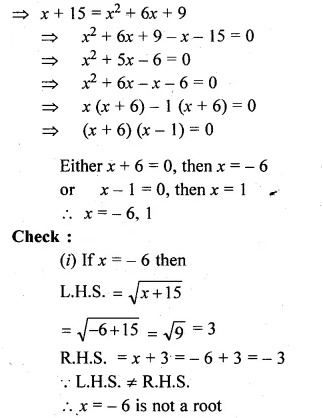
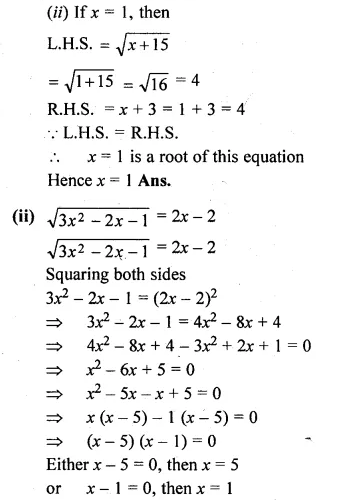
Solve the following equations (5 to 8) by using formula :

Question 5.
(i) 2x² – 3x – 1 = 0
(ii) \(x\left( 3x+\frac { 1 }{ 2 } \right) =6\)
Solution:
(i) 2x² – 3x – 1 = 0
Here a = 2, b = -3, c = -1

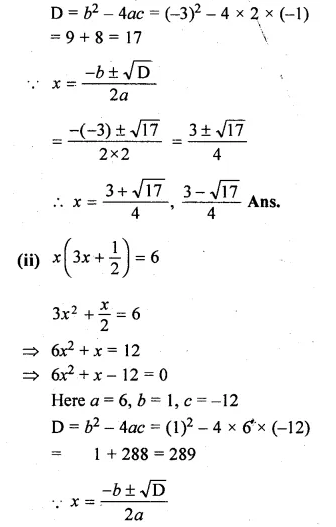
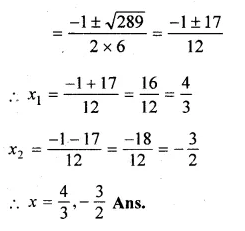
Question 6.
(i) \(\frac { 2x+5 }{ 3x+4 } =\frac { x+1 }{ x+3 } \)
(ii) \(\frac { 2 }{ x+2 } -\frac { 1 }{ x+1 } =\frac { 4 }{ x+4 } -\frac { 3 }{ x+3 } \)
Solution:
(i) \(\frac { 2x+5 }{ 3x+4 } =\frac { x+1 }{ x+3 } \)
(2x + 5)(x + 3) = (x + 1)(3x + 4)

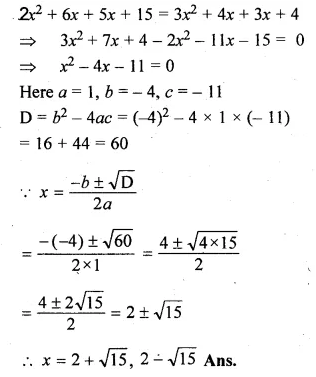
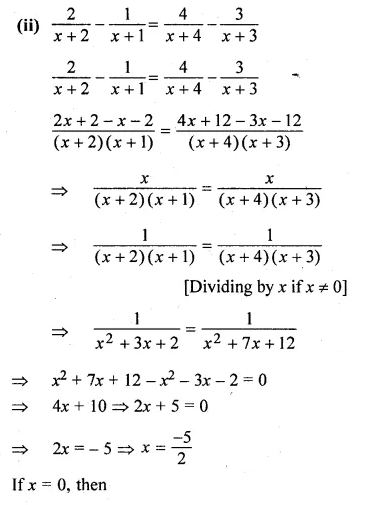
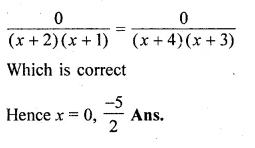
Question 7.
(i) \(\frac { 3x-4 }{ 7 } +\frac { 7 }{ 3x-4 } =\frac { 5 }{ 2 } ,x\neq \frac { 4 }{ 3 } \)
(ii) \(\frac { 4 }{ x } -3=\frac { 5 }{ 2x+3 } ,x\neq 0,-\frac { 3 }{ 2 } \)
Solution:
(i) \(\frac { 3x-4 }{ 7 } +\frac { 7 }{ 3x-4 } =\frac { 5 }{ 2 } ,x\neq \frac { 4 }{ 3 } \)
let \(\frac { 3x-4 }{ 7 } \) = y,then

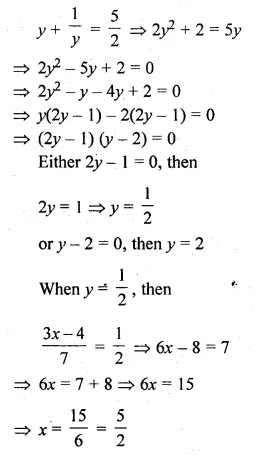
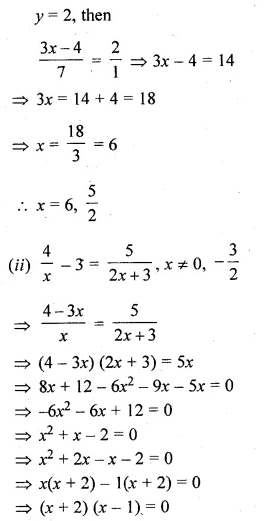
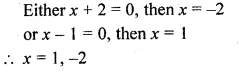
Question 8.
(i)x² + (4 – 3a)x – 12a = 0
(ii)10ax² – 6x + 15ax – 9 = 0,a≠0
Solution:
(i)x² + (4 – 3a)x – 12a = 0
Here a = 1, b = 4 – 3a, c = -12a

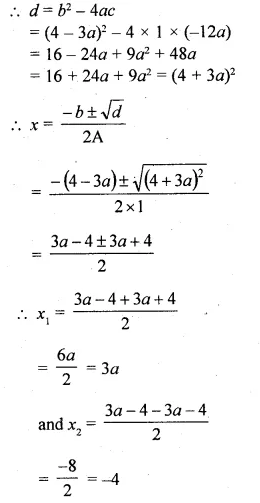
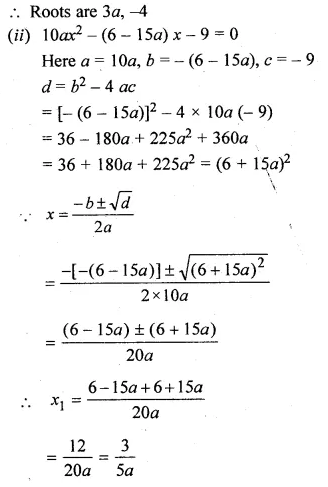
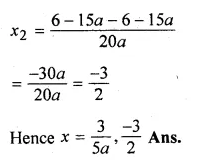
Question 9.
Solve for x using the quadratic formula. Write your answer correct to two significant figures: (x – 1)² – 3x + 4 = 0. (2014)
Solution:
(x – 1)² – 3x + 4 = 0
x² + 1 – 2x – 3x + 4 = 0

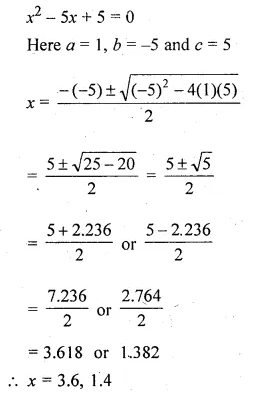
Question 10.
Discuss the nature of the roots of the following equations:
(i) 3x² – 7x + 8 = 0
(ii) x² – \(\\ \frac { 1 }{ 2 } x\) – 4 = 0
(iii) 5x² – 6√5x + 9 = 0
(iv) √3x² – 2x – √3 = 0
Solution:
(i) 3x² – 7x + 8 = 0
Here a = 3, b = -7, c = 8

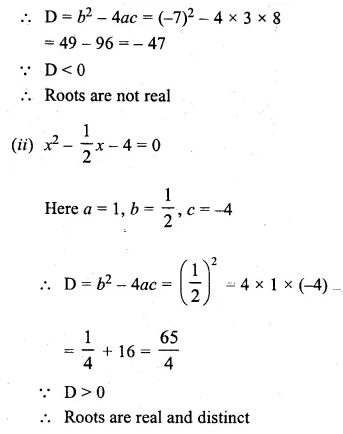
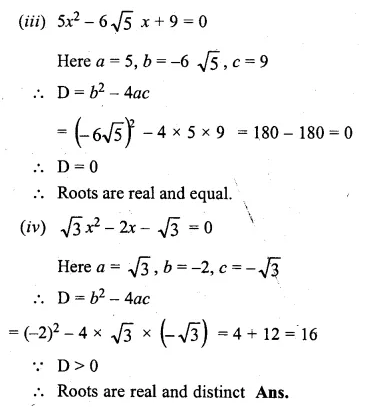
Question 11.
Find the values of k so that the quadratic equation (4 – k) x² + 2 (k + 2) x + (8k + 1) = 0 has equal roots.
Solution:
(4 – k) x² + 2 (k + 2) x + (8k + 1) = 0
Here a = (4 – k), b = 2 (k + 2), c = 8k + 1

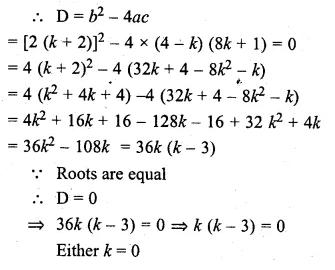
or k – 3 = 0, then k= 3
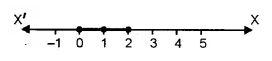
k = 0, 3 Ans.

Question 12.
Find the values of m so that the quadratic equation 3x² – 5x – 2m = 0 has two distinct real roots.
Solution:
3x² – 5x – 2m = 0
Here a = 3, b = -5, c = -2m

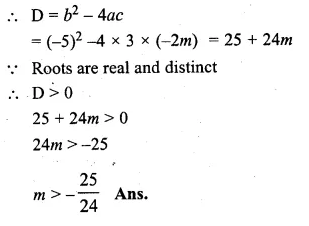
Question 13.
Find the value(s) of k for which each of the following quadratic equation has equal roots:
(i)3kx² = 4(kx – 1)
(ii)(k + 4)x² + (k + 1)x + 1 =0
Also, find the roots for that value (s) of k in each case.
Solution:
(i)3kx² = 4(kx – 1)
⇒ 3kx² = 4kx – 4
⇒ 3kx² – 4kx + 4 = 0

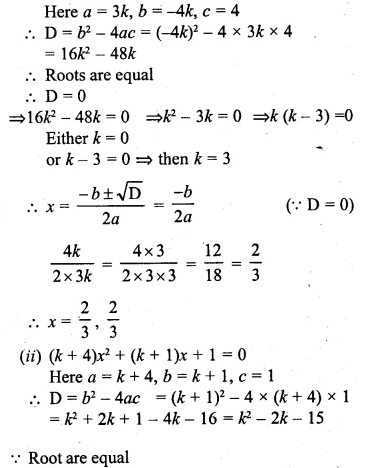
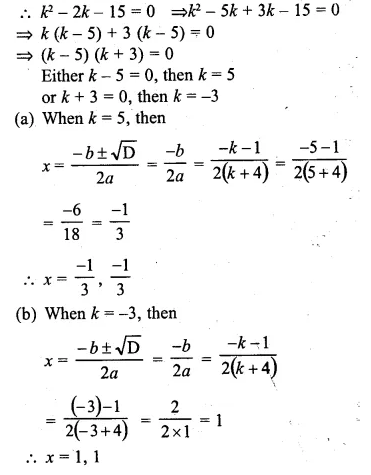
Question 14.
Find two natural numbers which differ by 3 and whose squares have the sum 117.
Solution:
Let first natural number = x
then second natural number = x + 3
According to the condition :
x² + (x + 3)² = 117

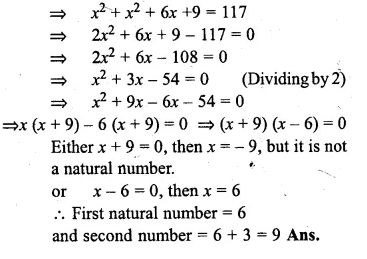
Question 15.
Divide 16 into two parts such that the twice the square of the larger part exceeds the square of the smaller part by 164.
Solution:
Let larger part = x
then smaller part = 16 – x
(∵ sum = 16)
According to the condition

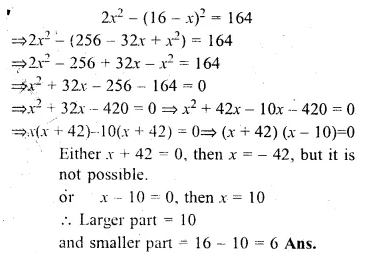
Question 16.
Two natural numbers are in the ratio 3 : 4. Find the numbers if the difference between their squares is 175.
Solution:
Ratio in two natural numbers = 3 : 4
Let the numbers be 3x and 4x
According to the condition,

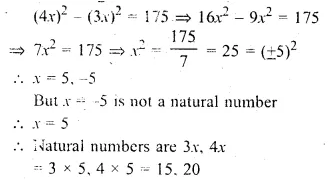
Question 17.
Two squares have sides A cm and (x + 4) cm. The sum of their areas is 656 sq. cm.Express this as an algebraic equation and solve it to find the sides of the squares.
Solution:
Side of first square = x cm .
and side of second square = (x + 4) cm
Now according to the condition,

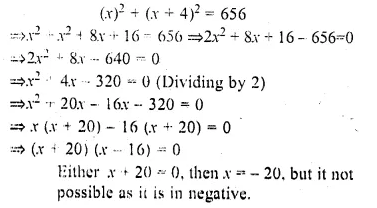
or x – 16 = 0 then x = 16
Side of first square = 16 cm
and side of second square = 16 + 4 – 4 = 20 cm

Question 18.
The length of a rectangular garden is 12 m more than its breadth. The numerical value of its area is equal to 4 times the numerical value of its perimeter. Find the dimensions of the garden.
Solution:
Let breadth = x m
then length = (x + 12) m
Area = l × b = x (x + 12) m²
and perimeter = 2 (l + b) = 2(x + 12 + x) = 2 (2x + 12) m
According to the condition.

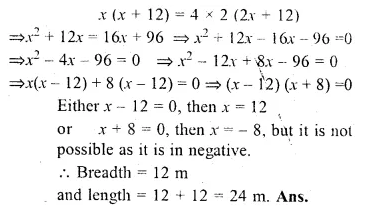
Question 19.
A farmer wishes to grow a 100 m² rectangular vegetable garden. Since he has with him only 30 m barbed wire, he fences three sides of the rectangular garden letting compound wall of his house act as the fourth side fence. Find the dimensions of his garden.
Solution:
Area of rectangular garden = 100 cm²
Length of barbed wire = 30 m
Let the length of the side opposite to wall = x

Question 20.
The hypotenuse of a right-angled triangle is 1 m less than twice the shortest side. If the third side is 1 m more than the shortest side, find the sides of the triangle.
Solution:
Let the length of shortest side = x m
Length of hypotenuse = 2x – 1
and third side = x + 1
Now according to the condition,

Question 21.
A wire ; 112 cm long is bent to form a right angled triangle. If the hypotenuse is 50 cm long, find the area of the triangle.
Solution:
Perimeter of a right angled triangle = 112 cm
Hypotenuse = 50 cm
∴ Sum of other two sides = 112 – 50 = 62 cm
Let the length of first side = x
and length of other side = 62 – x

Question 22.
Car A travels x km for every litre of petrol, while car B travels (x + 5) km for every litre of petrol.
(i) Write down the number of litres of petrol used by car A and car B in covering a distance of 400 km.
(ii) If car A uses 4 litres of petrol more than car B in covering 400 km. write down an equation, in A and solve it to determine the number of litres of petrol used by car B for the journey.
Solution:
Distance travelled by car A in one litre = x km
and distance travelled by car B in one litre = (x + 5) km
(i) Consumption of car A in covering 400 km

Question 23.
The speed of a boat in still water is 11 km/ hr. It can go 12 km up-stream and return downstream to the original point in 2 hours 45 minutes. Find the speed of the stream
Solution:
Speed of a boat in still water = 11 km/hr
Let the speed of stream = x km/hr.
Distance covered = 12 km.
Time taken = 2 hours 45 minutes

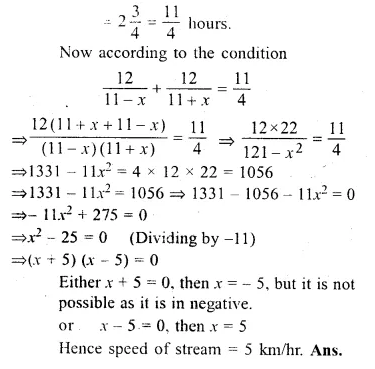
Question 24.
By selling an article for Rs. 21, a trader loses as much per cent as the cost price of the article. Find the cost price.
Solution:
S.P. of an article = Rs. 21
Let cost price = Rs. x
Then loss = x%

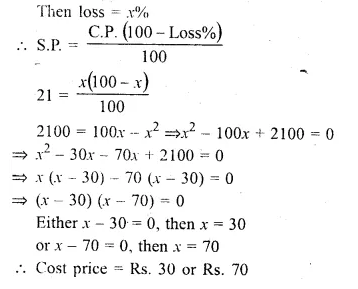
Question 25.
A man spent Rs. 2800 on buying a number of plants priced at Rs x each. Because of the number involved, the supplier reduced the price of each plant by Rupee 1.The man finally paid Rs. 2730 and received 10 more plants. Find x.
Solution:
Amount spent = Rs. 2800
Price of each plant = Rs. x
Reduced price = Rs. (x – 1)

Question 26.
Forty years hence, Mr. Pratap’s age will be the square of what it was 32 years ago. Find his present age.
Solution:
Let Partap’s present age = x years
40 years hence his age = x + 40
and 32 years ago his age = x – 32
According to the condition

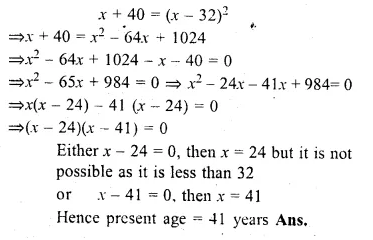
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Ex 3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Ex 3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Ex 3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Chapter Test

Question 1.
Find the dividend received on 60 shares of Rs, 20 each if 9% dividend is declared.
Solution:
Value of one share = Rs. 20
Value of 60 shares = Rs. 20 x 60
= Rs. 1200

Question 2.
A company declares 8 percent dividend to the share holders. If a man receives Rs. 2840 as his dividend, find the nominal value of his shares.
Solution:
Rate of dividend = 8%
Amount of dividend = Rs. 2840

Question 3.
A man buys 200 ten-rupee shares at Rs 12.50 each and receives a dividend of 8%. Find the amount invested by him and the dividend received by him in cash.
Solution:
Face value of 200 shares = Rs. 10 x 200
= Rs. 2000
(i) Amount invested for the purchase of 200 shares at the rate of Rs. 12.50 each
= Rs. 12.50 x 200
= Rs. 2500

NCVT MIS

Question 4.
Find the market price of 5% share when a person gets a dividend of Rs 65 by investing Rs. 1430.
Solution:
Amount of dividend = Rs. 65
Rate of dividend = 5%

Question 5.
Salman buys 50 shares of face value Rs 100 available at Rs 132.
(i) What is his investment ?
(ii) If the dividend is 7.5% p.a., what will be his annual income ?
(iii) If he wants to increase his annual income by Rs 150, how many extra shares should he
Solution:
Face Value = Rs 100
(i) Market Value = Rs 132
No. of shares = 50
Investment = no. of shares x Market value
= 50 x 132 = Rs 6600

Question 6.
A lady holds 1800, Rs. 100 shares of a company that pays 15% dividend annually. Calculate her annual dividend. If she had bought these shares at 40% premium, what percentage return does she get on her investment ? Give your answer to the nearest integer.
Solution:
Total number of shares = 1800
Nominal value of each share = Rs. 100
Rate of dividend = 15%

Question 7.
What sum should a person invest in Rs 25 shares, selling at Rs 36, to obtain an income of Rs 720, if the dividend declared is 12%? Also find the percentage return on his income.
(i) The number of shares bought by him.
(ii) The percentage return on his income.
Solution:
Nominal value of each share = Rs. 25
Market value of each share = Rs. 36

Question 8.
Ashok invests Rs 26400 on 12% Rs 25 shares of a company. If he receives a dividend of Rs 2475, find:
(i) the number of shares he bought.
(ii) the market value of each share. (2016)
Solution:
Investment = Rs 26400
Face value of each share = Rs 25
Rate of dividend = 12%
and total dividend = Rs 2475
We know,

Question 9.
Amit Kumar invests Rs 36,000 in buying Rs 100 shares at Rs 20 premium. The dividend is 15% per annum. Find :
(i) The number of shares he buys
(ii) His yearly dividend
(iii) The percentage return on his investment.
Give your answer correct to the nearest whole number.
Solution:
Investment = Rs 36000
Face value = Rs 100
Premium = Rs 20, dividend = 15%

Question 10.
Mr. Tiwari invested Rs 29,040 in 15% Rs 100 shares at a premium of 20%. Calculate:
(i) The number of shares bought by Mr. Tiwari.
(ii) Mr. Tiwari’s income from the investment.
(iii) The percentage return on his investment.
Solution:
(i) M.V. of one share = \(\left[ \frac { 20 }{ 100 } \times 100+100 \right] \)
= Rs 120

Question 11.
A man buys shares at the par value of Rs 10 yielding 8% dividend at the end of a year. Find the number of shares bought if he receives a dividend of Rs 300.
Solution:
Face value of each share = Rs 10
Rate of dividend = 8% p.a.
Total dividend = Rs 300

Question 12.
A man invests Rs 8800 on buying shares of face value of rupees hundred each at a premium of 10%. If he earns Rs 1200 at the end of year as dividend, find :
(i) the number of shares he has in the company.
(ii) the dividend percentage per share.
Solution:
Investment = Rs 8800
Face value of each share = Rs 100
and market value of each share
= Rs 100 + Rs 10 = Rs 110
Total income = Rs 1200
Total face value
= Rs \(\\ \frac { 8800\times 100 }{ 110 } \)
= Rs 8000

Question 13.
A man invested Rs. 45000 in 15% Rs. 100 shares quoted at Rs. 125. When the market value of these shares rose to Rs. 140, he sold some shares, just enough to raise Rs. 8400. Calculate :
(i) the number of shares he still holds.(2004)
(ii) the dividend due to him on these shares.
Solution:
Investment on shares = Rs. 45000
Face value of each share = Rs. 125

Question 14.
A company pays a dividend of 15% on its ten-rupee shares from which it deducts tax at the rate of 22%. Find the annual income of a man, who owns one thousand shares of this company.
Solution:
No. of shares = 1000
Face value of each are = Rs. 10
Rate of dividend = 15%,
Rate of tax deducted = 22%
Total face value of 1000 shares = Rs. 10 x 1000 = Rs. 10000
Total dividend = Rs 10000 x \(\\ \frac { 15 }{ 100 } \)
= Rs 1500
Tax deducted at the rate of 22 %

Question 15.
Ajay owns 560 shares of a company. The face value of each share is Rs. 25. The company declares a dividend of 9%. Calculate.
(i) the dividend that Ajay will get.
(ii) the rate of interest, on his investment if Ajay has paid Rs. 30 for each share. (2007)
Solution:
No. of shares = 560
Face value of each share = Rs. 25
Rate of dividend = 9% p.a.
Total face value of 560 shares = Rs. 25 x 560
= Rs. 14000

Question 16.
A company with 10000 shares of nominal value of Rs. 100 declares an annual dividend of 8% to the share holders.
(i) Calculate the total amount of dividend paid by the company.
(ii) Ramesh bought 90 shares of the company at Rs. 150 per share.
Calculate the dividend he received and the percentage return on his investment. (1994)
Solution:
(i) Number of shares = 10000
Nominal value of each share = Rs. 100
Rate of annual dividend = 8%
Total face value of 10000 shares
= Rs. 100 x 10000
= Rs. 1000000
and amount dividend = Rs \(\\ \frac { 1000000\times 8 }{ 100 } \)
= Rs 80000
(ii) Number of shares = 90
Face value of each share = Rs. 150
Total face value of 90 shades

Question 17.
A company with 4000 shares of nominal value of Rs. 110 declares annual dividend of 15%. Calculate :
(i) the total amount of dividend paid by the company,
(ii) the annual income of Shah Rukh who holds 88 shares in the company,
(iii) if he received only 10% on his investment, find the price Shah Rukh paid for each share. (2008)
Solution:
Number of shares = 4000
Nominal (face) value of each share = Rs. 110
Total face value of 4000 shares = Rs. 110 x 4000
= Rs, 440000
Rate of annual dividend = 15%

Question 18.
By investing Rs. 7500 in a company paying 10 percent dividend, an income of Rs. 500 is received. What price is paid for each Rs. 100 share
Solution:
Investment = Rs. 7500
Rate of dividend = 10%,
Total income = Rs. 500.
Face value of each share = Rs. 100
Total face value = \(\\ \frac { 100\times 500 }{ 10 } \) = Rs. 5000
If face value is Rs. 5000, then investment = Rs. 7500
and if face value is Rs. 100 then market value of

Question 19.
A man invests Rs. 8000 in a company paying 8% dividend when a share of face value of Rs. 100 is selling at Rs. 60 premium,
(i) What is his annual income,
(ii) What percent does he get on his money ?
Solution:
Investment = Rs. 8000
Face value of each share = Rs. 100
Market value = Rs. 100 + Rs. 60
= Rs. 160
Rate of dividend = 8% p.a.

Question 20.
A man buys 400 ten-rupee shares at a premium of Rs. 2.50 on each share. If the rate of dividend is 8%, Find,
(i) his investment
(ii) dividend received
(iii) yield.
Solution:
No. of shares = 400
Face value of each share = Rs. 10
Market value of each share
= Rs. 10 + Rs. 2.50
= Rs. 12.50
Rate of dividend = 8%

Question 21.
A man invests Rs. 10400 in 6% shares at Rs. 104 and Rs. 11440 in 10.4% shares at Rs. 143. How much income would he get in all ?
Solution:
In first case; Total investment = Rs. 10400
Rate of dividend = 6%
Market value of each share = Rs. 104

Total dividend from both cases = Rs. 600 + Rs. 832
= Rs. 1432 Ans.

Question 22.
Two companies have shares of 7% at Rs. 116 and 9% at Rs. 145 respectively. In which of the shares would the investment be more profitable ?
Solution:
Let the investment in each case = Rs. 116 x 145
Dividend in first case

Question 23.
Which is better investment : 6% Rs. 100 shares at Rs. 120 or 8% Rs. 10 shares at Rs. 15
Solution:
Let the investment in each case = Rs. 120 In the fist case,
Dividend on Rs. 120 = Rs. 6
In second case, Dividend on Rs. 10

Question 24.
A man invests Rs -10080 in 6% hundred- rupee shares at Rs. 112. Find his annual income. When the shares fall to Rs. 96 he sells out the shares and invests the proceeds in 10% ten-rupee shares at Rs. 8. Find the change in his annual income.
Solution:
Investment = Rs. 10080
Face value of each share = Rs. 100
Market value of each share = Rs. 112
Rate of dividend = 6%
Total income for the year

Question 25.
A man bought 360 ten-rupee shares paying 12% per annum. He sold them when the price rose to Rs. 21 and invested the proceeds in five-rupee shares paying \(4 \frac { 1 }{ 2 } \) % per annum at Rs. 3.5 per share. Find the annual change in his income.
Solution:
No. of shares bought = 360
Face value of each share = Rs. 10
Rate of dividend = 12%
Total face value of 360 shares
= Rs. 10 x 360
= Rs. 3600

Question 26.
A person invests Rs. 4368 and buys certain hundred-rupee shares at 91. He sells out shares worth Rs. 2400 when they have t risen to 95 and the remainder when they have fallen to 85. Find the gain or loss on the total transaction,
Solution:
Investment = Rs. 4368
Market value of each share = Rs. 91
Face value of each share = Rs. 100

Question 27.
By purchasing Rs. 50 gas shares for Rs. 80 each, a man gets 4% profit on his investment. What rate percent is company paying ? What is his dividend if he buys 200 shares ?
Solution:
Market value of each share = Rs 80
Face value of each share = Rs. 50
Interest on investment = 4%

Dividend = Rs 10000 x \(\\ \frac { 6.4 }{ 100 } \)
= Rs 640

Question 28.
Rs. 100 shares of a company are sold at a discount of Rs. 20. If the return on the investment is 15%. Find the rate of dividend declared
Solution:
Market value of each shares = 100 – 20
= Rs.80
Interest on investment of Rs. 80
= 15% x 80
= \(\\ \frac { 15 }{ 100 } \) x 80
= Rs 12
Dividend on face value of Rs. 100 = Rs. 12
Rate of dividend = 12%. Ans.

Question 29.
A company declared a dividend of 14%. Find tire market value of Rs. 50 shares if the return on the investment was 10%.
Solution:
Rate of dividend = 14%
Dividend on Rs. 50 = \(\\ \frac { 14\times 50 }{ 100 } \) = Rs 7
Now Rs. 10 is interest on the investment of
= Rs. 100
Rs. 7 will be the interest on
= \(\\ \frac { 100\times 7 }{ 10 } \) = Rs. 70
Hence Market value of Rs. 50 shares = Rs. 70Ans.

Question 30.
At what price should a 6.25% Rs. 100 shares be quoted when the money is worth 5%?
Solution:
Interest on Rs. 100 worth = Rs. 5
If interest is Rs. 5, then market value = Rs. 100
and if interest is Rs. 6.25, then market value

Market value of each share = Rs. 125 Ans.

Question 31.
At what price should a 6.25% Rs. 50 share be quoted when the money is worth 10%?
Solution:
Interest on Rs. 100
worth = Rs. 10
If the interest is Rs. 10, then market value = Rs. 100
and if interest is Rs. 6.25, then market

Question 32.
A company with 10000 shares of Rs. 100 each, declares an annual dividend of 5%.
(i) What is the total amount of dividend paid by the company ?
(ii) What would be the annual income of a man, who has 72 shares, in the company ?
(iii) If he received only 4% on his investment, find the price he paid for each share. (1998)
Solution:
No. of shares = 10000
Face value of each share = Rs. 100
Rate of dividend = 5%
(i) Total face value of 10000 shares
= Rs. 100 x 10000
= Rs. 1000000

Question 33.
A man sold some Rs. 100 shares paying 10% dividend at a discount of 25% and invested the proceeds in Rs. 100 shares paying 16% dividend quoted at Rs. 80 and thus increased his income by Rs. 2000. Find the number of shares sold by him.
Solution:
Face value of each share = Rs. 100
Market value of each share
= Rs. 100 – Rs.25
= Rs. 75
Rate of dividend = 10%
Let no. of shares = x
Selling price = x × 75 =Rs. 75x
Face value of x share = 100 x

Question 34.
By selling at Rs. 77, some \(2 \frac { 1 }{ 4 } \) % shares of face value Rs. 100, and investing the proceeds in 6% shares of face value Rs. 100, selling at 110, a person increased his income by Rs, 117 per annum. How many shares did he sell ?
Solution:
Let the number of shares = x
On selling at Rs.77, the amt received x × 77 = Rs. 77 x

Question 35.
A man invests Rs. 6750, partly in shares of 6% at Rs. 140 and partly in shares of 5% at Rs. 125. If his total income is Rs. 280, how much has he invested in each ?
Solution:
Let the investment in first case = x
Then investment in second case = (6750 – x)
In first case, the dividend

Question 36.
Divide Rs. 20304 into two parts such that if one part is invested in 9% Rs. 50 shares at 8% premium and the other part is invested in 8% Rs. 25 shares at 8% discount, then the annual incomes from both the investment are equal
Solution:
Total amount = Rs 20304
Let amount invested in 9% Rs 50 at 8%
premium = x
Then amount invested in 8% Rs 25 at 8%
Discount = 20304 – x
Income from both investments are equal Now income from first type of shares

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Ex 3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking EX 2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking Chapter Test

Question 1.
Mr. Dhruv deposits Rs 600 per month in a recurring deposit account for 5 years at the rate of 10% per annum (simple interest). Find the amount he will receive at the time of maturity.
Solution:
Deposit per month = Rs 600
Rate of interest = 10% p.a.
Period (n) = 5 years 60 months.
Total principal for one month

Question 2.
Ankita started paying Rs 400 per month in a 3 years recurring deposit. After six months her brother Anshul started paying Rs 500 per month in a \(2 \frac { 1 }{ 2 } \) years recurring deposit. The bank paid 10% p.a. simple interest for both. At maturity who will get more money and by how much?
Solution:
In case of Ankita,
Deposit per month = Rs 400
Period (n) = 3 years = 36 months
Rate of interest = 10%
Total principal for one month

Question 3.
Shilpa has a 4 year recurring deposit account in Bank of Maharashtra and deposits Rs 800 per month. If she gets Rs 48200 at the time of maturity, find
(i) the rate of simple interest,
(ii) the total interest earned by Shilpa
Solution:
Deposit per month (P) = Rs 800
Amount of maturity = Rs 48200

Question 4.
Mr. Chaturvedi has a recurring deposit account in Grindlay’s Bank for \(4 \frac { 1 }{ 2 } \) years at 11% p.a. (simple interest). If he gets Rs 101418.75 at the time of maturity, find the monthly instalment.
Solution:
Let each monthly instalment = Rs x
Rate of interest = 11 %
Period (n) = \(4 \frac { 1 }{ 2 } \) years or 54 months,
Total principal for one month

Question 5.
Rajiv Bhardwaj has a recurring deposit account in a bank of Rs 600 per month. If the bank pays simple interest of 7% p.a. and he gets Rs 15450 as maturity amount, find the total time for which the account was held.
Solution:
Deposit during the month (P) = Rs 600
Rate of interest = 7% p.a.
Amount of maturity = Rs 15450
Let time = n months

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test

Question 1.
Solve the inequation : 5x – 2 ≤ 3(3 – x) where x ∈ { – 2, – 1, 0, 1, 2, 3, 4}. Also represent its solution on the number line.
Solution:
5x – 2 < 3(3 – x)
⇒ 5x – 2 ≤ 9 – 3x
⇒ 5x + 3x ≤ 9 + 2

Question 2.
Solve the inequations :
6x – 5 < 3x + 4, x ∈ I.
Solution:
6x – 5 < 3x + 4
6x – 3x < 4 + 5
⇒ 3x <9
⇒ x < 3
x ∈ I
Solution Set = { -1, -2, 2, 1, 0….. }

Question 3.
Find the solution set of the inequation
x + 5 < 2 x + 3 ; x ∈ R
Graph the solution set on the number line.
Solution:
x + 5 ≤ 2x + 3
x – 2x ≤ 3 – 5
⇒ -x ≤ -2
⇒ x ≥ 2

Question 4.
If x ∈ R (real numbers) and – 1 < 3 – 2x ≤ 7, find solution set and represent it on a number line.
Solution:
-1 < 3 – 2x ≤ 7
-1 < 3 – 2x and 3 – 2x ≤ 7
⇒ 2x < 3 + 1 and – 2x ≤ 7 – 3
⇒ 2x < 4 and -2x ≤ 4
⇒ x < 2 and -x ≤ 2
and x ≥ -2 or -2 ≤ x
x ∈ R
Solution set -2 ≤ x < 2
Solution set on number line

Question 5.
Solve the inequation :
\(\frac { 5x+1 }{ 7 } -4\left( \frac { x }{ 7 } +\frac { 2 }{ 5 } \right) \le 1\frac { 3 }{ 5 } +\frac { 3x-1 }{ 7 } ,x\in R\)
Solution:
\(\frac { 5x+1 }{ 7 } -4\left( \frac { x }{ 7 } +\frac { 2 }{ 5 } \right) \le 1\frac { 3 }{ 5 } +\frac { 3x-1 }{ 7 } \)
\(\frac { 5x+1 }{ 7 } -4\left( \frac { x }{ 7 } +\frac { 2 }{ 5 } \right) \le \frac { 8 }{ 5 } +\frac { 3x-1 }{ 7 } \)

Question 6.
Find the range of values of a, which satisfy 7 ≤ – 4x + 2 < 12, x ∈ R. Graph these values of a on the real number line.
Solution:
7 < – 4x + 2 < 12
7 < – 4x + 2 and – 4x + 2 < 12

Question 7.
If x∈R, solve \(2x-3\ge x+\frac { 1-x }{ 3 } >\frac { 2 }{ 5 } x\)
Solution:
\(2x-3\ge x+\frac { 1-x }{ 3 } >\frac { 2 }{ 5 } x\)
\(2x-3\ge x+\frac { 1-x }{ 3 } \) and \(x+\frac { 1-x }{ 3 } >\frac { 2 }{ 5 } x\)

Question 8.
Find positive integers which are such that if 6 is subtracted from five times the integer then the resulting number cannot be greater than four times the integer.
Solution:
Let the positive integer = x
According to the problem,
5a – 6 < 4x
⇒ 5a – 4x < 6
⇒ x < 6
Solution set = {x : x < 6}
= { 1, 2, 3, 4, 5, 6}

Question 9.
Find three smallest consecutive natural numbers such that the difference between one-third of the largest and one-fifth of the smallest is at least 3.
Solution:
Let first least natural number = x
then second number = x + 1
and third number = x + 2

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking EX 2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking Chapter Test

Choose the correct answer from the given four options (1 to 4) :

Question 1.
If Sharukh opened a recurring deposit account in a bank and deposited Rs 800 per month for \(1 \frac { 1 }{ 2 } \) years, then the total money
deposited in the account is
(a) Rs 11400
(b) Rs 14400
(c) Rs 13680
(d) none of these
Solution:
Monthly deposit = Rs800
Period (n) = \(1 \frac { 1 }{ 2 } \) years = 18 months
.’. Total money deposit = Rs 800 x 18
= Rs 14400 (b)

Question 2.
Mrs. Asha Mehta deposit Rs 250 per month for one year in a bank’s recurring deposit account. If the rate of (simple) interest is 8% per annum, then the interest earned by her on this account is
(a) Rs 65
(b) Rs 120
(c) Rs 130
(d) Rs 260
Solution:
Deposit per month (P) = Rs 250
Period (n) = 1 year = 12 months
Rate (r) = 8% p.a.

Question 3.
Mr. Sharma deposited Rs 500 every month in a cumulative deposit account for 2 years. If the bank pays interest at the rate of 7% per annum, then the amount he gets on maturity is
(a) Rs 875
(b) Rs 6875
(c) Rs 10875
(d) Rs 12875
Solution:
Deposit (P) = Rs 500 per month
Period (n) = 2 years = 24 months
Rate (r) = 7% p.a.

Question 4.
John deposited Rs 400 every month in a bank’s recurring deposit account for \(2 \frac { 1 }{ 2 } \) years. If he gets Rs 1085 as interest at the time of maturity, then the rate of interest per annum is
(a) 6%
(b) 7%
(c) 8%
(d) 9%
Solution:
Deposit (P) = Rs 400 per month
Period (n) = \(2 \frac { 1 }{ 2 } \) years = 3 months
Interest = Rs 1085
Let r% be the rate of interest

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 2 Banking MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test

Choose the correct answer from the given four options (1 to 5) :

Question 1.
If x ∈ { – 3, – 1, 0, 1, 3, 5}, then the solution set of the inequation 3x – 2 ≤ 8 is
(a) { – 3, – 1, 1, 3}
(b) { – 3, – 1, 0, 1, 3}
(c) { – 3, – 2, – 1, 0, 1, 2, 3}
(d) { – 3, – 2, – 1, 0, 1, 2}
Solution:
x ∈ { -3, -1, 0, 1, 3, 5}
3x – 2 ≤ 8
⇒ 3x ≤ 8 + 2
⇒ 3x ≤ 10
⇒ x ≤ \(\\ \frac { 10 }{ 3 } \)
⇒ x < \(3 \frac { 1 }{ 3 } \)
Solution set = { -3, -1, 0, 1, 3} (b)

Question 2.
If x ∈ W, then the solution set of the inequation 3x + 11 ≥ x + 8 is
(a) { – 2, – 1, 0, 1, 2, …}
(b) { – 1, 0, 1, 2, …}
(c) {0, 1, 2, 3, …}
(d) {x : x∈R,x≥\(– \frac { 3 }{ 2 } \)}
Solution:
x ∈ W
3x + 11 ≥ x + 8
⇒ 3x – x ≥ 8 – 11

Question 3.
If x ∈ W, then the solution set of the inequation 5 – 4x ≤ 2 – 3x is
(a) {…, – 2, – 1, 0, 1, 2, 3}
(b) {1, 2, 3}
(c) {0, 1, 2, 3}
(d) {x : x ∈ R, x ≤ 3}
Solution:
x ∈ W
5 – 4x < 2 – 3x
⇒ 5 – 2 ≤ 3x + 4x
⇒ 3 ≤ x
Solution set = {0, 1, 2, 3,} (c)

Question 4.
If x ∈ I, then the solution set of the inequation 1 < 3x + 5 ≤ 11 is
(a) { – 1, 0, 1, 2}
(b) { – 2, – 1, 0, 1}
(c) { – 1, 0, 1}
(d) {x : x ∈ R, \(– \frac { 4 }{ 3 } \) < x ≤ 2}
Solution:
x ∈ I
1 < 3x + 5 ≤ 11
⇒ 1 < 3x + 5
⇒ 1 – 5 < 3x

Question 5.
If x ∈ R, the solution set of 6 ≤ – 3 (2x – 4) < 12 is
(a) {x : x ∈ R, 0 < x ≤ 1}
(b) {x : x ∈ R, 0 ≤ x < 1}
(c) {0, 1}
(d) none of these
Solution:
x ∈ R
6 ≤ – 3(2x – 4) < 12
⇒ 6 ≤ – 3(2x – 4)
⇒ 6 ≤ – 6x + 12

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Chapter Test

Question 1.
Solve the inequation 3x -11 < 3 where x ∈ {1, 2, 3,……, 10}. Also represent its solution on a number line
Solution:
3x – 11 < 3 => 3x < 3 + 11 => 3x < 14 x < \(\\ \frac { 14 }{ 3 } \)
But x ∈ 6 {1, 2, 3, ……., 10}
Solution set is (1, 2, 3, 4}
Ans. Solution set on number line

Question 2.
Solve 2(x – 3)< 1, x ∈ {1, 2, 3, …. 10}
Solution:
2(x – 3) < 1 => x – 3 < \(\\ \frac { 1 }{ 2 } \) => x < \(\\ \frac { 1 }{ 2 } \) + 3 => x < \(3 \frac { 1 }{ 2 } \)
But x ∈ {1, 2, 3 …..10}
Solution set = {1, 2, 3} Ans.

Question 3.
Solve : 5 – 4x > 2 – 3x, x ∈ W. Also represent its solution on the number line.
Solution:
5 – 4x > 2 – 3x
– 4x + 3x > 2 – 5
=> – x > – 3
=> x < 3
x ∈ w,
solution set {0, 1, 2}
Solution set on Number Line :

Question 4.
List the solution set of 30 – 4 (2.x – 1) < 30, given that x is a positive integer.
Solution:
30 – 4 (2x – 1) < 30
30 – 8x + 4 < 30
– 8x < 30 – 30 – 4
– 8x < – 4 x > \(\\ \frac { -4 }{ -8 } \)
=> x > \(\\ \frac { 1 }{ 2 } \)
x is a positive integer
x = {1, 2, 3, 4…..} Ans.

Question 5.
Solve : 2 (x – 2) < 3x – 2, x ∈ { – 3, – 2, – 1, 0, 1, 2, 3} .
Solution:
2(x – 2) < 3x – 2
=> 2x – 4 < 3x – 2
=> 2x – 3x < – 2 + 4
=> – x < 2
=> x > – 2
Solution set = { – 1, 0, 1, 2, 3} Ans.

Question 6.
If x is a negative integer, find the solution set of \(\\ \frac { 2 }{ 3 } \)+\(\\ \frac { 1 }{ 3 } \) (x + 1) > 0.
Solution:
\(\\ \frac { 2 }{ 3 } \)+\(\\ \frac { 1 }{ 3 } \) x + \(\\ \frac { 1 }{ 3 } \) > 0
=> \(\\ \frac { 1 }{ 3 } \) x + 1 > 0
=> \(\\ \frac { 1 }{ 3 } \) x > – 1

x is a negative integer
Solution set = {- 2, – 1} Ans.

Question 7.
Solve: \(\\ \frac { 2x-3 }{ 4 } \)≥\(\\ \frac { 1 }{ 2 } \), x ∈ {0, 1, 2,…,8}
Solution:
\(\\ \frac { 2x-3 }{ 4 } \)≥\(\\ \frac { 1 }{ 2 } \)
=> 2x – 3 ≥ \(\\ \frac { 4 }{ 2 } \)

Question 8.
Solve x – 3 (2 + x) > 2 (3x – 1), x ∈ { – 3, – 2, – 1, 0, 1, 2, 3}. Also represent its solution on the number line.
Solution:
x – 3 (2 + x) > 2 (3x – 1)
=> x – 6 – 3x > 6x – 2
=> x – 3x – 6x > – 2 + 6
=> – 8x > 4
=> x < \(\\ \frac { -4 }{ 8 } \) => x < \(– \frac { 1 }{ 2 } \)
x ∈ { – 3, – 2, – 1, 0, 1, 2}
.’. Solution set = { – 3, – 2, – 1}
Solution set on Number Line :

Question 9.
Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9} solve x – 3 < 2x – 1.
Solution:
x – 3 < 2x – 1
x – 2x < – 1 + 3 => – x < 2 x > – 2
But x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Solution set = {1, 2, 3, 4, 5, 6, 7, 9} Ans.

Question 10.
Given A = {x : x ∈ I, – 4 ≤ x ≤ 4}, solve 2x – 3 < 3 where x has the domain A Graph the solution set on the number line.
Solution:
2x – 3 < 3 => 2x < 3 + 3 => 2x < 6 => x < 3
But x has the domain A = {x : x ∈ I – 4 ≤ x ≤ 4}
Solution set = { – 4, – 3, – 2, – 1, 0, 1, 2}
Solution set on Number line :

Question 11.
List the solution set of the inequation
\(\\ \frac { 1 }{ 2 } \) + 8x > 5x \(– \frac { 3 }{ 2 } \), x ∈ Z
Solution:
\(\\ \frac { 1 }{ 2 } \) +8x > 5x \(– \frac { 3 }{ 2 } \)

Question 12.
List the solution set of \(\\ \frac { 11-2x }{ 5 } \) ≥ \(\\ \frac { 9-3x }{ 8 } \) + \(\\ \frac { 3 }{ 4 } \),
x ∈ N
Solution:
\(\\ \frac { 11-2x }{ 5 } \) ≥ \(\\ \frac { 9-3x }{ 8 } \) + \(\\ \frac { 3 }{ 4 } \)
=> 88 – 16x ≥ 45 – 15x + 30
(L.C.M. of 8, 5, 4 = 40}
=> – 16x + 15x ≥ 45 + 30 – 88
=> – x ≥ – 13
=>x ≤ 13
x ≤ N.
Solution set = {1, 2, 3, 4, 5, .. , 13} Ans.

Question 13.
Find the values of x, which satisfy the inequation : \(-2\le \frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le 1\frac { 5 }{ 6 } \), x ∈ N.
Graph the solution set on the number line. (2001)
Solution:
\(-2\le \frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le 1\frac { 5 }{ 6 } \), x ∈ N

Question 14.
If x ∈ W, find the solution set of
\(\frac { 3 }{ 5 } x-\frac { 2x-1 }{ 3 } >1\)
Also graph the solution set on the number line, if possible.
Solution:
\(\frac { 3 }{ 5 } x-\frac { 2x-1 }{ 3 } >1\)
9x – (10x – 5) > 15 (L.C.M. of 5, 3 = 15)
=> 9x – 10x + 5 > 15
=> – x > 15 – 5
=> – x > 10
=> x < – 10
But x ∈ W
Solution set = Φ
Hence it can’t be represented on number line.

Question 15.
Solve:
(i)\(\frac { x }{ 2 } +5\le \frac { x }{ 3 } +6\) where x is a positive odd integer.
(ii)\(\frac { 2x+3 }{ 3 } \ge \frac { 3x-1 }{ 4 } \) where x is positive even integer.
Solution:
(i) \(\frac { x }{ 2 } +5\le \frac { x }{ 3 } +6\)

Question 16.
Given that x ∈ I, solve the inequation and graph the solution on the number line :
\(3\ge \frac { x-4 }{ 2 } +\frac { x }{ 3 } \ge 2 \) (2004)
Solution:
\(3\ge \frac { x-4 }{ 2 } +\frac { x }{ 3 } \) and \(3\ge \frac { x-4 }{ 2 } +\frac { x }{ 3 } \ge 2 \)

Question 17.
Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9}, find the values of x for which -3 < 2x – 1 < x + 4.
Solution:
-3 < 2x – 1 < x + 4.
=> – 3 < 2x – 1 and 2x – 1 < x + 4
=> – 2x < – 1 + 3 and 2x – x < 4 + 1
=> – 2x < 2 and x < 5
=> – x < 1
=> x > – 1
– 1 < x < 5
x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Solution set = {1, 2, 3, 4} Ans.

Question 18.
Solve : 1 ≥ 15 – 7x > 2x – 27, x ∈ N
Solution:
1 ≥ 15 – 7x > 2x – 27
1 ≥ 15 – 7x and 15 – 7x > 2x – 27

Question 19.
If x ∈ Z, solve 2 + 4x < 2x – 5 ≤ 3x. Also represent its solution on the number line.
Solution:
2 + 4x < 2x – 5 ≤ 3x
2 + 4x < 2x – 5 and 2x – 5 ≤ 3x => 4x – 2x < – 5 – 2 ,and 2x – 3x ≤ 5

Question 20.
Solve the inequation = 12 + \(1 \frac { 5 }{ 6 } x\) ≤ 5 + 3x, x ∈ R. Represent the solution on a number line. (1999)
Solution:
12 + \(1 \frac { 5 }{ 6 } x\) ≤ 5 + 3x

Question 21.
Solve : \(\\ \frac { 4x-10 }{ 3 } \)≤\(\\ \frac { 5x-7 }{ 2 } \) x ∈ R and represent the solution set on the number line.
Solution:
\(\\ \frac { 4x-10 }{ 3 } \)≤\(\\ \frac { 5x-7 }{ 2 } \)
=> 8x – 20 ≤ 15x – 21
(L.C.M. of 3, 2 = 6)

Question 22.
Solve \(\frac { 3x }{ 5 } -\frac { 2x-1 }{ 3 } \) > 1, x ∈ R and represent the solution set on the number line.
Solution:
\(\frac { 3x }{ 5 } -\frac { 2x-1 }{ 3 } \) > 1
=> 9x – (10x – 5) > 15
=> 9x – 10x + 5 > 15
=> – x > 15 – 5
=> – x > 10
=> x < – 10
x ∈ R.
.’. Solution set = {x : x ∈R, x < – 10}
Solution set on the number line

Question 23.
Solve the inequation – 3 ≤ 3 – 2x < 9, x ∈ R. Represent your solution on a number line. (2000)
Solution:
– 3 ≤ 3 – 2x < 9
– 3 ≤ 3 – 2x and 3 – 2x < 9
2x ≤ 3 + 3 and – 2x < 9 – 3
2x ≤ 6 and – 2x < 6 => x ≤ 3 and – x < 3 => x ≤ – 3 and – 3 < x
– 3 < x ≤ 3.
Solution set= {x : x ∈ R, – 3 < x ≤ 3)
Solution on number line

Question 24.
Solve 2 ≤ 2x – 3 ≤ 5, x ∈ R and mark it on number line. (2003)
Solution:
2 ≤ 2x – 3 ≤ 5 .
2 ≤ 2x – 3 and 2x – 3 ≤ 5
2 + 3 ≤ 2x and 2x ≤ 5 + 3
5 ≤ 2x and 2x ≤ 8.

Question 25.
Given that x ∈ R, solve the following inequation and graph the solution on the number line: – 1 ≤ 3 + 4x < 23. (2006)
Solution:
We have
– 1 ≤ 3 + 4x < 23 => – 1 – 3 ≤ 4x < 23 – 3 => – 4 ≤ 4x < 20 => – 1 ≤ x < 5, x ∈ R
Solution Set = { – 1 ≤ x < 5; x ∈ R}

Question 26.
Solve tlie following inequation and graph the solution on the number line. (2007)
\(-2\frac { 2 }{ 3 } \le x+\frac { 1 }{ 3 } <3+\frac { 1 }{ 3 } \) x∈R
Solution:
Given \(-2\frac { 2 }{ 3 } \le x+\frac { 1 }{ 3 } <3+\frac { 1 }{ 3 } \) x∈R
\(-\frac { 8 }{ 3 } \le x+\frac { 1 }{ 3 } <\frac { 10 }{ 3 } \)
Multiplying by 3, L.C.M. of fractions, we get

Question 27.
Solve the following inequation and represent the solution set on the number line :
\(-3<-\frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le \frac { 5 }{ 6 } ,x\in R\)
Solution:
\(-3<-\frac { 1 }{ 2 } -\frac { 2x }{ 3 } \le \frac { 5 }{ 6 } ,x\in R\)

Question 28.
Solve \(\frac { 2x+1 }{ 2 } +2(3-x)\ge 7,x\in R\). Also graph the solution set on the number line
Solution:
\(\frac { 2x+1 }{ 2 } +2(3-x)\ge 7,x\in R\)

Question 29.
Solving the following inequation, write the solution set and represent it on the number line. – 3(x – 7)≥15 – 7x > \(\\ \frac { x+1 }{ 3 } \), n ∈R
Solution:
– 3(x – 7)≥15 – 7x > \(\\ \frac { x+1 }{ 3 } \), n ∈R

Question 30.
Solve the inequation :
\(-2\frac { 1 }{ 2 } +2x\le \frac { 4x }{ 3 } \le \frac { 4 }{ 3 } +2x,\quad x\in W\). Graph the solution set on the number line.
Solution:
\(-2\frac { 1 }{ 2 } +2x\le \frac { 4x }{ 3 } \le \frac { 4 }{ 3 } +2x,\quad x\in W\)

Question 31.
Solve the inequation 2x – 5 ≤ 5x + 4 < 11, where x ∈ I. Also represent the solution set on the number line. (2011)
Solution:
2x – 5 ≤ 5x + 4 < 11 2x – 5 ≤ 5x + 4
=> 2x – 5 – 4 ≤ 5x and 5x + 4 < 11
=> 2x – 9 ≤ 5x and 5x < 11 – 4
and 5x < 7
=> 2x – 5x ≤ 9 and x < \(\\ \frac { 7 }{ 5 } \)
=> 3x > – 9 and x< 1.4
=> x > – 3

Question 32.
If x ∈ I, A is the solution set of 2 (x – 1) < 3 x – 1 and B is the solution set of 4x – 3 ≤ 8 + x, find A ∩B.
Solution:
2 (x – 1) < 3 x – 1
2x – 2 < 3x – 1
2x – 3x < – 1 + 2 => – x < 1 x > – 1
Solution set A = {0, 1, 2, 3, ..,.}
4x – 3 ≤ 8 + x
4x – x ≤ 8 + 3
=> 3x ≤ 11
=> x ≤ \(\\ \frac { 11 }{ 3 } \)
Solution set B = {3, 2, 1, 0, – 1…}
A ∩ B = {0, 1, 2, 3} Ans.

Question 33.
If P is the solution set of – 3x + 4 < 2x – 3, x ∈ N and Q is the solution set of 4x – 5 < 12, x ∈ W, find
(i) P ∩ Q
(ii) Q – P.
Solution:
(i) – 3 x + 4 < 2 x – 3
– 3x – 2x < – 3 – 4 => – 5x < – 7

Question 34.
A = {x : 11x – 5 > 7x + 3, x ∈R} and B = {x : 18x – 9 ≥ 15 + 12x, x ∈R}
Find the range of set A ∩ B and represent it on a number line
Solution:
A = {x : 11x – 5 > 7x + 3, x ∈R}
B = {x : 18x – 9 ≥ 15 + 12x, x ∈R}
Now, A = 11x – 5 > 7x + 3
=> 11x – 7x > 3 + 5
=> 4x > 8
=>x > 2, x ∈ R

Question 35.
Given: P {x : 5 < 2x – 1 ≤ 11, x∈R)
Q{x : – 1 ≤ 3 + 4x < 23, x∈I) where
R = (real numbers), I = (integers)
Represent P and Q on number line. Write down the elements of P ∩ Q. (1996)
Solution:
P= {x : 5 < 2x – 1 ≤ 11}
5 < 2x – 1 ≤ 11

Question 36.
If x ∈ I, find the smallest value of x which satisfies the inequation \(2x+\frac { 5 }{ 2 } >\frac { 5x }{ 3 } +2\)
Solution:
\(2x+\frac { 5 }{ 2 } >\frac { 5x }{ 3 } +2\)
=>\(2x-\frac { 5x }{ 3 } >2-\frac { 5 }{ 2 } \)
=>12x – 10x > 12 – 15
=> 2x > – 3
=>\(x>-\frac { 3 }{ 2 } \)
Smallest value of x = – 1 Ans.

Question 37.
Given 20 – 5 x < 5 (x + 8), find the smallest value of x, when
(i) x ∈ I
(ii) x ∈ W
(iii) x ∈ N.
Solution:
20 – 5 x < 5 (x + 8)
⇒ 20 – 5x < 5x + 40
⇒ – 5x – 5x < 40 – 20
⇒ – 10x < 20
⇒ – x < 2
⇒ x > – 2
(i) When x ∈ I, then smallest value = – 1.
(ii) When x ∈ W, then smallest value = 0.
(iii) When x ∈ N, then smallest value = 1. Ans.

Question 38.
Solve the following inequation and represent the solution set on the number line :
\(4x-19<\frac { 3x }{ 5 } -2\le -\frac { 2 }{ 5 } +x,x\in R\)
Solution:
We have
\(4x-19<\frac { 3x }{ 5 } -2\le -\frac { 2 }{ 5 } +x,x\in R\)
Hence, solution set is {x : -4 < x < 5, x ∈ R}
The solution set is represented on the number line as below.

Question 39.
Solve the given inequation and graph the solution on the number line :
2y – 3 < y + 1 ≤ 4y + 7; y ∈ R.
Solution:
2y – 3 < y + 1 ≤ 4y + 7; y ∈ R.
(a) 2y – 3 < y + 1
⇒ 2y – y < 1 + 3
⇒ y < 4
⇒ 4 > y ….(i)
(b) y + 1 ≤ 4y + 7

Question 40.
Solve the inequation and represent the solution set on the number line.
\(-3+x\le \frac { 8x }{ 3 } +2\le \frac { 14 }{ 3 } +2x,Where\quad x\in I\)
Solution:
Given : \(-3+x\le \frac { 8x }{ 3 } +2\le \frac { 14 }{ 3 } +2x,Where\quad x\in I\)

Question 41.
Find the greatest integer which is such that if 7 is added to its double, the resulting number becomes greater than three times the integer.
Solution:
Let the greatest integer = x
According to the condition,
2x + 7 > 3x
⇒ 2x – 3x > – 7
⇒ – x > – 7
⇒ x < 7
Value of x which is greatest = 6 Ans.

Question 42.
One-third of a bamboo pole is buried in mud, one-sixth of it is in water and the part above the water is greater than or equal to 3 metres. Find the length of the shortest pole.
Solution:
Let the length of the shortest pole = x metre
Length of pole which is burried in mud = \(\\ \frac { x }{ 3 } \)
Length of pole which is in the water = \(\\ \frac { x }{ 6 } \)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 4 Linear Inequations Ex 4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends EX 3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Chapter Test

Question 1.
If a man received ₹1080 as dividend from 9% ₹20 shares, find the number of shares purchased by him.
Solution:
Income on one share = \(\\ \frac { 9 }{ 100 } \) x 20
= Rs \(\\ \frac { 9 }{ 5 } \)
.’. No. of shares = 1080 x \(\\ \frac { 5 }{ 9 } \)
= 120 x 5 = 600 Ans.

Question 2.
Find the percentage interest on capital invested in 18% shares when a Rs 10 share costs Rs 12.
Solution:
Dividend on one share = 18% of Rs 10
= \(\\ \frac { 18\times 10 }{ 100 } \)
= Rs \(\\ \frac { 9 }{ 5 } \)

Question 3.
Rohit Kulkami invests Rs 10000 in 10% Rs 100 shares of a company. If his annual dividend is Rs 800, find :
(i) The market value of each share.
(ii) The rate percent which he earns on his investment.
Solution:
Investment = Rs 10000
Face value of each share = Rs 100
Rate of dividend = 10%
Annual dividend = Rs 800

Question 4.
At what price should a 9% Rs 100 share be quoted when the money is worth 6% ?
Solution:
If interest is 6 then investment = Rs 100
and if interest is 9, then investment
= Rs \(\\ \frac { 100\times 9 }{ 6 } \)
= Rs 150
Market value of each share = Rs 150 Ans

Question 5.
By selling at Rs 92, some 2.5% Rs 100 shares and investing the proceeds in 5% Rs 100 shares at Rs 115, a person increased his annual income by Rs 90. Find:
(i) the number of shares sold.
(ii) the number of shares purchased.
(iii) the new income.
(iv) the rate percent which he earns on his investment.
Solution:
Rate of dividend = 2.5% and market price = Rs 92
Let number of shares purchased = x.
Selling price of x shares = 92 x
Income from investing

Question 6.
A man has some shares of Rs. 100 par value paying 6% dividend. He sells half of these at a discount of 10% and invests the proceeds in 7% Rs. 50 shares at a premium of Rs. 10. This transaction decreases his income from dividends by Rs. 120. Calculate:
(i) the number of shares before the transaction.
(ii) the number of shares he sold.
(iii) his initial annual income from shares.
Solution:
Let no. of shares = x
Value of x shares = x × 100 = 100 x

Question 7.
Divide Rs. 101520 into two parts such that if one part is invested in 8% Rs. 100 shares at 8% discount and the other in 9% Rs. 50 shares at 8% premium, the annual incomes are equal.
Solution:
Total investment = Rs. 101520
Let investment in first part = x
and in second part = (101520 – x)
Market value of first kind of shares = Rs. 100 – Rs. 8
= Rs. 92
and rate of dividend = 8%

Question 8.
A man buys Rs. 40 shares of a company which pays 10% dividend. He buys the shares at such a price that his profit is 16% on his investment. At what price did he buy each share ?
Solution:
Face value of each share = Rs. 40
Dividend = 10%
Gain on investment = 10%

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends EX 3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends Chapter Test

Question 1.
If Jagbeer invest ₹10320 on ₹100 shares at a discount of ₹ 14, then the number of shares he buys is
(a) 110
(b) 120
(c) 130
(d) 150
Solution:
Investment = ₹ 10320
Face value of each share = ₹100
M.V. of each share = ₹100 – 14 = ₹86
No. of shares = \(\\ \frac { 10320 }{ 86 } \) = 120 (b)

Question 2.
If Nisha invests ₹19200 on ₹50 shares at a premium of 20%, then the number of shares she buys is
(a) 640
(b) 384
(c) 320
(d) 160
Solution:
Investment = ₹19200
Face value of each share = ₹50
M.V. = ₹50 x \(\\ \frac { 120 }{ 100 } \) = ₹60
Number of shares = \(\\ \frac { 19200 }{ 60 } \)
= 320 (c)

Question 3.
₹40 shares of a company are selling at 25% premium. If Mr. Jacob wants to buy 280 shares of the company, then the investment required by him is
(a) ₹11200
(b) ₹14000
(c) ₹16800
(d) ₹8400
Solution:
Face value of each share = ₹40
M.V. = 40 x \(\\ \frac { 125 }{ 100 } \)= ₹50
Number of shares = 280
Total investment = ₹280 x 50 = ₹ 14000 (d)

Question 4.
Arun possesses 600 shares of ₹25 of a company. If the company announces a dividend of 8%, then Arun’s annual income is
(a) ₹48
(b) ₹480
(c) ₹600
(d) ₹1200
Solution:
Number of shares = 600
F.V. of each share = ₹25
Rate of dividend = 8%
Annual income = 600 x 25 x \(\\ \frac { 8 }{ 100 } \)
= ₹1200 (d)

Question 5.
A man invests ₹24000 on ₹60 shares at a discount of 20%. if the dividend declared by the company is 10%, then his annual income is
(a) ₹3000
(b) ₹2880
(c) ₹ 1500
(d) 1440
Solution:
Investment = ₹24000
F.V. of each share = ₹60
M.V. at discount of 20% = 60 x \(\\ \frac { 80 }{ 100 } \)= ₹48
Rate of dividend = 10%

Question 6.
Salman has some shares of ₹50 of a company paying 15% dividend. If his annual income is ₹3000, then the number of shares he possesses is
(a) 80
(b) 400
(c) 600
(d) 800
Solution:
F.V. of each share = ₹50
Dividend = 15%
Annual income = ₹3000
Let x be the share, then
F.V. of shares = x × 50 = ₹50x

Question 7.
₹25 shares of a company are selling at ₹20. If the company is paying a dividend of 12%, then the rate of return is
(a) 10%
(b) 12%
(c) 15%
(d) 18%
Solution:
F.V. of each share = ₹25 ,
M.V. = ₹20
Rate of dividend = 12%
Dividend on each share = \(\\ \frac { 12 }{ 100 } \) x 25 = ₹3
Return on ₹20 = ₹3
and on ₹100 = ₹ \(\\ \frac { 3 }{ 20 } \) x \(\\ \frac { 5 }{ 100 } \) = 15% (c)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 3 Shares and Dividends MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Chapter Test

Question 1.
Draw an equilateral triangle of side 4 cm. Draw its circumcircle.

Solution:
Steps of Construction :
(i) Draw a line segment BC = 4 cm
(ii) With centres B and C, draw two arcs of radius 4 cm
which intersect each other at A.
(iii) Join AB and AC. ∆ ABC is an equilateral triangle.
(iv) Draw the right bisector of BC and AC intersecting each other at O.
(v) Join OA, OB and OC.
(vi) With centre O, and radius equal to OB or OC or OA,
draw a circle which will pass through A, B and C.
This is the required circumcircle of ∆ ABC.

Question 2.
Using a ruler and a pair of compasses only, construct: (i) a triangle ABC given AB = 4cm, BC = 6 cm and ∠ABC = 90°.
(ii) a circle which passes through the points A, B and C and mark its centre as O. (2008)
Solution:
Steps of Construction:
(i) Draw a line segment AB = 4cm
(ii) At B, draw a ray BX making an angle of 90°
and cut off BC = 6 cm.
(iii) Join AC.
(iv) Draw the perpendicular bisectors of sides
AB and AC intersecting each other at O.
(v) With centre O, and radius equal to OB or OA or OC,
draw a circle which passes through A, B and C.
This is the required circle.

Question 3.
Construct a triangle with sides 3 cm, 4 cm and 5 cm. Draw its circumcircle and measure its radius.
Solution:
Steps of Construction
(i) Draw a line segment BC = 4 cm.
(ii) With centre B and radius 3 cm and with centre C
and radius 5 cm draw two arcs which intersect each other at A.
(iii) Join AB and AC.
(iv) Draw the perpendicular bisector of sides BC and AC
which intersect each other at O.
(v) Join OB.
(vi) With centre O and radius OB, draw a circle
which will pass through A, B and C.
(vii) On measuring the radius OB = 2.5cm

Question 4.
Using ruler and compasses only :
(i) Construe a triangle ABC with the following data: Base AB = 6 cm, AC = 5.2 cm and ∠CAB = 60°.
(ii) In the same diagram, draw a circle which passes through the points A, B and C. and mark its centre O.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 6 cm.
(ii) At A, draw a ray making an angle of 60°.
(iii) With centre B and radius 5-2 cm.
draw an arc which intersects the ray at C.
(iv) Join BC
(v) Draw the perpendicular bisector of AB and BC
intersecting each other at O.
(vi) With O as a centre and OA as a radius
draw a circle which touches the ∆ABC at A, B and C.

Question 5.
Using ruler and compasses only, draw an equilateral triangle of side 5 cm and draw its inscribed circle. Measure the radius of the circle.
Solution:
Steps of Construction :
(i). Draw a line segment BC = 5 cm
(ii) With centre B and C and radius 5 cm,
draw two arcs intersecting each other at A.
(iii) Join AB and AC.
(iv) Draw the angle bisectors of ∠B and ∠C intersecting each other at I.
(v) From I, draw a perpendicular ID on BC.
(vi) With centre I and radius ID, draw a circle
which touches the sides of the triangle internally.

This is the required in circle.
Measure the radius ID which is 1.5 cm (approx)

Question 6.
(i) Conduct a triangle ABC with BC = 6.4 cm, CA = 5.8 cm and ∠ ABC = 60°. Draw its incircle. Measure and record the radius of the incircle.
(ii) Construct a ∆ABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle. (2014)
Solution:
Steps of Construction :
(i) Draw a line segment BC = 6.4 cm
(ii) Construct ∠ DBC = 60° at B.
(iii) With C as centre and radius CA = 5.8 cm.
Draw an arc cutting BD at A.
(iv) Join AC. Then ABC is the required triangle.
(v) Draw the angle bisectors of ∠B and ∠C which intersect each other at O.
(vi) Draw OE ⊥ BC, intersecting BC in E.
(vii) With O as centre and OE as radius draw the required incircle.
Measure the radius OE which is = 1.5cm

Steps of construction:
1. Draw a line BC = 6.5 cm.
2. With centre B and C draw arcs AB = 5.5 cm and AC = 5 cm
3. Join AB and AC, ABC is the required triangle.
4. Draw the angle bisetors of B and C. Let these bisectors meet at O.
5. Taking O as centre. Draw a incircle which touches all the sides of the ∆ABC.
6. From O draw a perpendicular to side BC which cut at N.
7. Measure ON which is required radius of the incircle. ON = 1.5 cm

Question 7.
The bisectors of angles A and B of a scalene triangle ABC meet at O.
(i) What is the point O called?
(ii) OR and OQ are drawn a perpendicular to AB and CA respectively. What is the relation between OR and OQ ?
(iii) What is the relation between ∠ACO and ∠BCO?
Solution:
(i) The point O where the angle bisectors meet is called the incentre of the triangle.
(ii) The perpendiculars drawn from O to AB and CA are equal i.e. OR and OQ.
(iii) ∠ACO = ∠BCO
OC will bisect the ∠C

Question 8.
Using ruler and compasses only, construct a triangle ABC in which BC = 4 cm, ∠ACB = 45° and the perpendicular from A on BC is 2.5 cm. Draw the circumcircle of triangle ABC and measure its radius.
Solution:
Steps of Construction
(i) Draw a line segment BC = 4 cm.
(ii) At B, draw a perpendicular and cut off BE = 2.5 cm.

(iii) From E, draw a line EF parallel to BC.
(iv) From C, draw a ray making an angle of 45° which intersects EF at A.
(v) Join AB.
(vi) Draw the perpendicular bisectors of
sides BC and AC intersecting each other at O.
(vii) Join OB, OC and OA.
(viii) With centre 0 and radius OB or OC or OA draw a circle
which will pass through A, B and C.
This circle is the circumcircle of ∆ABC. On measuring its radius OB = 2 cm.

Question 9.
Construct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.

Solution:
Steps of Construction
(i) Draw a line segment BC = 4 cm.
(ii) At A and B draw rays making on angle of 120° each and cut off AF = BC = 4cm.
(iii) At F and C, draw rays making angle of 120° each and cut off EF = CD = 4cm.
(iv) Join ED.
ABCDEF is the required hexagon.
(v) Draw perpendicular bisectors of sides AB and BC intersecting each other at O.
(vi) With centre O and radius equal OA or OB draw a circle
which passes through the vertices of the hexagon.
This is the required circumcircle of hexagon ABCDEF.

Question 10.
Draw a regular hexagon of side 4 cm and construct its incircie.
Solution:
Steps of constructions :

(i) Draw a regular hexagon ABCDEF of side 4 cm.
(ii) Draw the angle bisectors of ∠A and ∠B
which intersect each other at O.
(iii) Draw OL ⊥ AB.
(iv) With centre O and radius OB, draw a circle
which touches the sides of the hexagon

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.1 More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Chapter Test

Question 1. Use a ruler and compass only in this question. (i) Draw a circle, centre O and radius 4 cm. (ii) Mark a point P such that OP = 7 cm. Construct the two tangents to the circle from P. Measure and record the length of one of the tangents. Solution: Steps of Construction:

1. Draw a circle with centre O and radius 4 cm.
2. Take a point P such that OP = 7 cm.
3. Bisect OB at M.
4. With centre M and diameter OP, draw another circle intersecting the given circle at A and B.
5. Join PA and PB. PA and PB is a pair of tangents to the circle.
6. On measuring PA, it is equal to 5.5 cm.

Question 2. Draw a line AB = 6 cm. Construct a circle with AB as diameter. Mark a point P at a distance of 5 cm from the mid-point of AB. Construct two tangents from P to the circle with AB as diameter. Measure the length of each tangent Solution: Steps of Construction:

1. Take a line segment AB = 6 cm.
2. Draw its perpendicular bisector bisecting it at O.
3. With centre O and radius OB, draw a circle.
4. Produce AB to P such that OP = 5 cm.
5. Draw its perpendicular bisector intersecting it at M.
6. With centre M and radius OM, draw a circle which intersects the given circle at T and S.
7. Join OT, OS, TP and SP. PT and PS are the required tangents to the given circle.
8. On measuring, each tangent is 4 cm long i.e. PT = PS = 4 cm.

Question 3. Construct a tangent to a circle of radius 4cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation. Solution: Steps of construction:

1. Take a point O.
2. With centre O and radii 4 cm and 6 cm, draw two concentric circles.
3. Join OA and take its mid-point M.
4. With centre M and radius MA, draw another circle which intersects the first circle at P and Q.
5. Join AP and AQ. AP and AQ are the required tangents to the first circle from point A.

Question 4. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q. Solution: Steps of construction:

1. Take a point O and with centre O, and radius 3 cm, draw a circle.
2. Produce its diameter both sides and cut off OP = OQ = 7 cm.
3. Take mid-points of OP and OQ as M and N respectively.
4. With centres M and N and OP and OQ as diameters, draw circles which intersect the given circle at A, B and C and D respectively.
5. Join PA, PB, QC and QD. PA, PB and QC and QD are the required tangents.

Question 5. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle. Solution: Steps of construction:

1. Draw a line segment AB = 8 cm.
2. With centre A and radius 4 cm and with centre B and radius 3 cm, draw circles.
3. Draw a third circle AB as diameter which intersects the given two circles at C and D and P and Q respectively.
4. Join AC and AD, BP and BQ.
5. AC and AD, BP and BQ are the required tangents.

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 16 Constructions Ex 16.1 are helpful to complete your math homework. If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.