ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test
Question 1.
Find the discriminant of the following equations and hence find the nature of roots:
(i) 3x² – 5x – 2 = 0
(ii) 2x² – 3x + 5 = 0
(iii) 7x² + 8x + 2 = 0
(iv) 3x² + 2x – 1 = 0
(v) 16x² – 40x + 25 = 0
(vi) 2x² + 15x + 30 = 0.
Solution:
(i) 3x² – 5x – 2 = 0
Here a = 3, b = -5, c = -2


Question 2.
Discuss the nature of the roots of the following quadratic equations :
(i) x² – 4x – 1 = 0
(ii) 3x² – 2x + \(\\ \frac { 1 }{ 3 } \) = 0
(iii) 3x² – 4√3x + 4 = 0
(iv) x² – \(\\ \frac { 1 }{ 2 } x\) + 4 = 0
(v) – 2x² + x + 1 = 0
(vi) 2√3x² – 5x + √3 = 0
Solution:
(i) x² – 4x – 1 = 0
Here a = 1, b = -4, c = -1
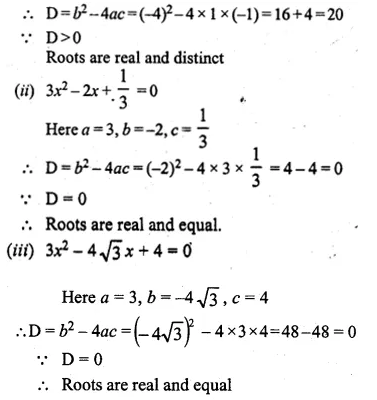
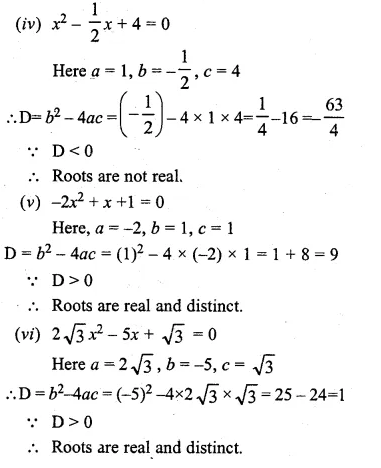
Question 3.
Find the nature of the roots of the following quadratic equations:
(i) x² – \(\\ \frac { 1 }{ 2 } x\) – \(\\ \frac { 1 }{ 2 } \) = 0
(ii) x² – 2√3x – 1 = 0 If real roots exist, find them.
Solution:
(i) x² – \(\\ \frac { 1 }{ 2 } x\) – \(\\ \frac { 1 }{ 2 } \) = 0
Here a = 1, b = \(– \frac { 1 }{ 2 } \), c = \(– \frac { 1 }{ 2 } \)
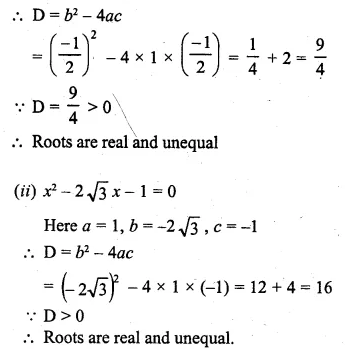
Question 4.
Without solving the following quadratic equation, find the value of ‘p’ for which the given equations have real and equal roots:
(i) px² – 4x + 3 = 0
(ii) x² + (p – 2)x + p = 0.
Solution:
(i) px² – 4x + 3 = 0
Here a = p, b = -4, c = 3
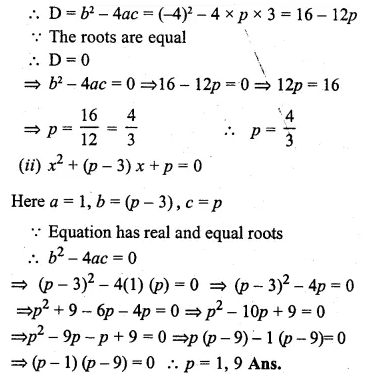
Question 5.
Find the value (s) of k for which each of the following quadratic equation has equal roots :
(i) kx² – 4x – 5 = 0
(ii) (k – 4) x² + 2(k – 4) x + 4 = 0
Solution:
(i) kx² – 4x – 5 = 0
Here a = k, b = -4, c = 5
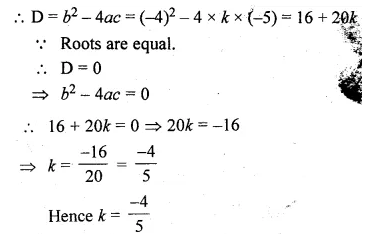
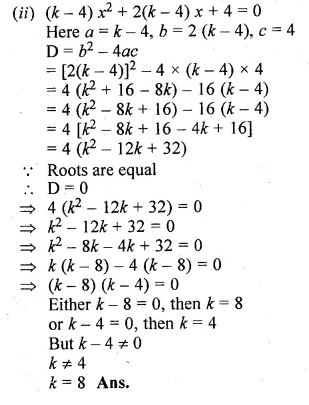
Question 6.
Find the value(s) of m for which each of the following quadratic equation has real and equal roots:
(i) (3m + 1)x² + 2(m + 1)x + m = 0
(ii) x² + 2(m – 1) x + (m + 5) = 0
Solution:
(i) (3m + 1)x² + 2(m + 1)x + m = 0
Here a = 3m + 1, b = 2(m + 1), c = m
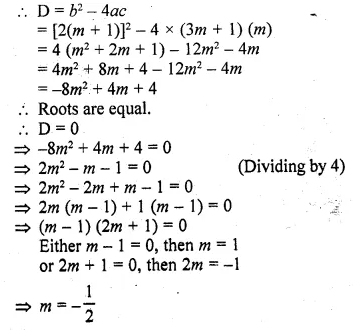
Question 7.
Find the values of k for which each of the following quadratic equation has equal roots:
(i) 9x² + kx + 1 = 0
(ii) x² – 2kx + 7k – 12 = 0
Also, find the roots for those values of k in each case.
Solution:
(i) 9x² + kx + 1 = 0
Here a = 9, b = k, c = 1
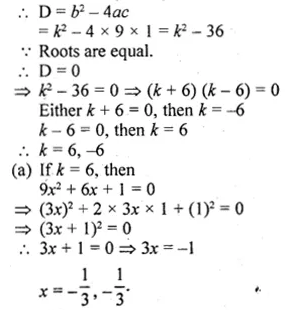
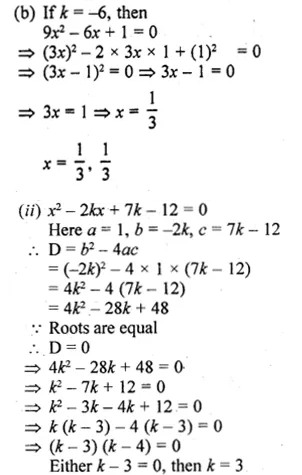
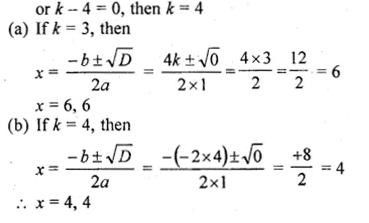
Question 8.
Find the value(s) of p for which the quadratic equation (2p + 1)x² – (7p + 2)x + (7p – 3) = 0 has equal roots. Also find these roots.
Solution:
The quadratic equation given is (2p + 1)x² – (7p + 2)x + (7p – 3) = 0
Comparing with ax² + bx + c = 0, we have
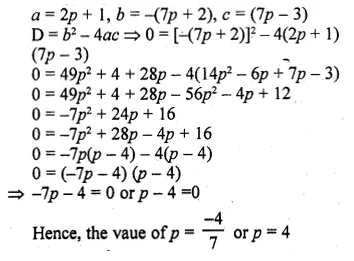
Question 9.
If – 5 is a root of the quadratic equation 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, find the value of k.
Solution:
-5 is a root of the quadratic equation
2x² + px – 15 = 0, then
⇒ 2(5)² – p( -5) – 15 = 0
⇒ 50 – 5p – 15 = 0
⇒ 35 – 5p = 0
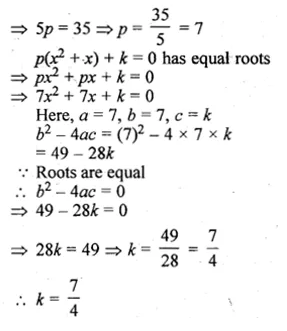
Question 10.
Find the value(s) of p for which the equation 2x² + 3x + p = 0 has real roots.
Solution:
2x² + 3x + p = 0
Here, a = 2, b = 3, c = p
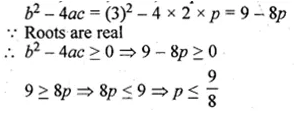
Question 11.
Find the least positive value of k for which the equation x² + kx + 4 = 0 has real roots.
Solution:
x² + kx + 4 = 0
Here, a = 1, b = k, c = 4
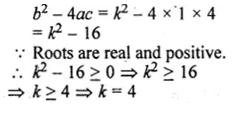
Question 12.
Find the values of p for which the equation 3x² – px + 5 = 0 has real roots.
Solution:
3x² – px + 5 = 0
Here, a = 3, b = -p, c = 5
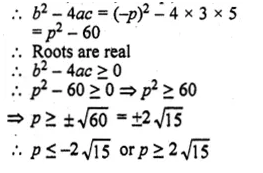
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.