NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Chapter Name | Polynomials |
| Exercise | Ex 2.4 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4
Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 – 5x + 2; \(\frac { 1 }{ 4 }\), 1, -2
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Solution:
(i) Comparing the given polynomial with ax3 + bx2 + cx + d, we get:
a = 2, b – 1, c = -5 and d = 2.
∴ p(x) = 2x3 + x2 – 5x + 2

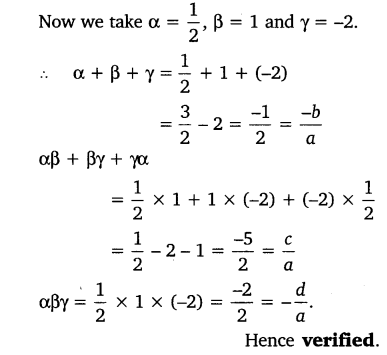
(ii) Compearing the given polynomial with ax3 + bx2 + cx + d, we get:
a = 1, b = -4, c = 5 and d = – 2.
∴ p (x) = x3 – 4x2 + 5x – 2
⇒ p(2) = (2)3 – 4(2)2 + 5 x 2 – 2
= 8 – 16+ 10 – 2 = 0
p(1) = (1)3 – 4(1)2 + 5 x 1-2
= 1 – 4 + 1 – 2
= 6-6 = 0
Hence, 2, 1 and 1 are the zeroes of x3 – 4x2 + 5x – 2.
Hence verified.
Now we take α = 2, β = 1 and γ = 1.
α + β + γ = 2 + 1 + 1 = \(\frac { 4 }{ 1 }\) = \(\frac { -b }{ a }\)
αβ + βγ + γα = 2 + 1 + 2 = \(\frac { 5 }{ 1 }\) = \(\frac { c }{ a }\)
αβγ = 2 x 1 x 1 = \(\frac { 2 }{ 1 }\) = \(\frac { -d }{ a }\).
Hence verified.
Question 2.
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:
Let α , β and γ be the zeroes of the required polynomial.
Then α + β + γ = 2, αβ + βγ + γα = -7 and αβγ = -14.
∴ Cubic polynomial
= x3 – (α + β + γ)x2 + (αβ + βγ + γα)x – αβγ
= x3 – 2x2 – 1x + 14
Hence, the required cubic polynomial is x3 – 2x2 – 7x + 14.
Question 3.
If the zeroes of the polynomial x3 – 3x2 + x + 1 are a-b, a, a + b, find a and b.
Solution:
Let α , β and γ be the zeroes of polynomial x3 – 3x2 + x + 1.
Then α = a-b, β = a and γ = a + b.
∴ Sum of zeroes = α + β + γ
⇒ 3 = (a – b) + a + (a + b)
⇒ (a – b) + a + (a + b) = 3
⇒ a-b + a + a + b = 3
⇒ 3a = 3
⇒ a = \(\frac { 3 }{ 3 }\) = 1 …(i)
Product of zeroes = αβγ
⇒ -1 = (a – b) a (a + b)
⇒ (a – b) a (a + b) = -1
⇒ (a2 – b2)a = -1
⇒ a3 – ab2 = -1 … (ii)
Putting the value of a from equation (i) in equation (ii), we get:
(1)3-(1)b2 = -1
⇒ 1 – b2 = -1
⇒ – b2 = -1 – 1
⇒ b2 = 2
⇒ b = ±√2
Hence, a = 1 and b = ±√2.
Question 4.
If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± √3, finnd other zeroes.
Solution:
Since two zeroes are 2 + √3 and 2 – √3,
∴ [x-(2 + √3)] [x- (2 – √3)]
= (x-2- √3)(x-2 + √3)
= (x-2)2– (√3)2
x2 – 4x + 1 is a factor of the given polynomial.
Now, we divide the given polynomial by x2 – 4x + 1.
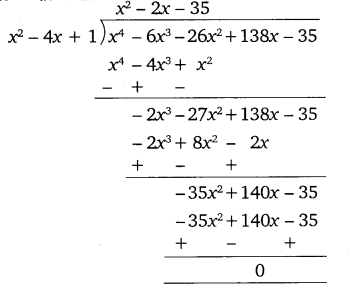
So, x4 – 6x3 – 26x2 + 138x – 35
= (x2 – 4x + 1) (x2 – 2x – 35)
= (x2 – 4x + 1) (x2 – 7x + 5x – 35)
= (x2-4x + 1) [x(x- 7) + 5 (x-7)]
= (x2 – 4x + 1) (x – 7) (x + 5)
Hence, the other zeroes of the given polynomial are 7 and -5.
Question 5.
If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:
We have
p(x) = x4 – 6x3 + 16x2 – 25x + 10
Remainder = x + a … (i)
Now, we divide the given polynomial 6x3 + 16x2 – 25x + 10 by x2 – 2x + k.
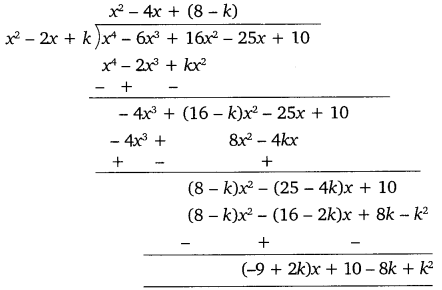
Using equation (i), we get:
(-9 + 2k)x + 10-8 k + k2 = x + a
On comparing the like coefficients, we have:
-9 + 2k = 1
⇒ 2k = 10
⇒ k = \(\frac { 10 }{ 2 }\) = 5 ….(ii)
and 10 -8k + k2– a ….(iii)
Substituting the value of k = 5, we get:
10 – 8(5) + (5)2 = a
⇒ 10 – 40 + 25 = a
⇒ 35 – 40 = a
⇒ a = -5
Hence, k = 5 and a = -5.
We hope the NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4, drop a comment below and we will get back to you at the earliest.