NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Number Systems |
| Exercise | Ex 1.5 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5
Question 1.
Classify the following numbers as rational or irrational.
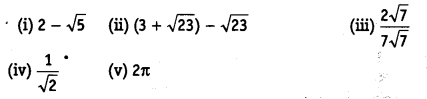
Solution:
(i) Irrational ∵ 2 is a rational number and √5 is an irrational number.
∴ 2.√5 is an irrational number.
(∵The difference of a rational number and an irrational number is irrational)
(ii) 3 + \( \sqrt{23} \) – \( \sqrt{23} \) = 3 (rational)
(iii) \(\frac { 2\sqrt { 7 } }{ 7\sqrt { 7 } }\) (rational)
(iv) \(\frac { 1 }{ \sqrt { 2 } }\)(irrational) ∵ 1 ≠ 0 is a rational number and \( \sqrt{2} \)≠ 0 is an irrational number.
∴ \(\frac { 1 }{ \sqrt { 2 } }\) is an irrational number. 42
(∵ The quotient of a non-zero rational number with an irrational number is irrational).
(v) 2π (irrational) ∵ 2 is a rational number and π is an irrational number.
∴ 2x is an irrational number. ( ∵The product of a non-zero rational number with an irrational number is an irrational)
Question 2.
Simplify each of the following expressions

Solution:
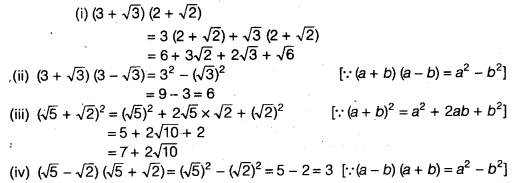
Question 3.
Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is π = \(\frac { c }{ d }\). This seems to contradict the fact that n is irrational. How will you resolve this contradiction?
Solution:
Actually \(\frac { c }{ d }\) = \(\frac { 22 }{ 7 }\),which is an approximate value of π.
Question 4.
Represent \( \sqrt{9.3} \) on the number line.
Solution:
Firstly we draw AB = 9.3 units. Now, from S, mark a distance of 1 unit. Let this point be C. Let O be the mid-point of AC. Now, draw aemi – circle with centre O and radius OA. Let us draw a line perpendicular to AC passing through point B and intersecting the semi-circle at point D.
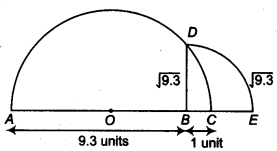
∴ The distance BD = \( \sqrt{9.3} \)
Draw an arc with centre B and radius BD, which intersects the number line at point E, then the point E represents \( \sqrt{9.3} \) .
Question 5.
Rationalise the denominator of the following
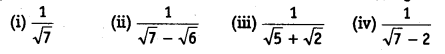
Solution:
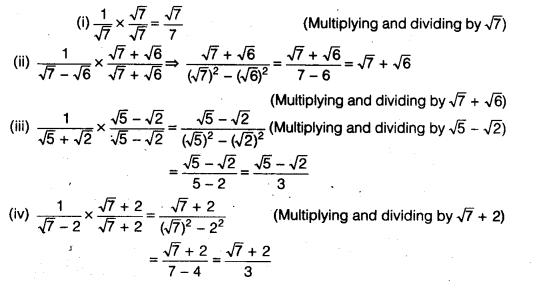
We hope the NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5, drop a comment below and we will get back to you at the earliest.