NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.4 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.4.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 11 |
| Chapter Name | Circles |
| Exercise | Ex 11.4 |
| Number of Questions Solved | 6 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.4
Question 1.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution:
Let O and O’ be the centres of the circles of radii 5 cm and 3 cm, respectively.
Let AB be their common chord.
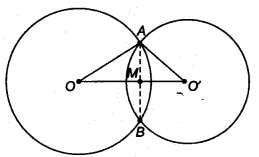
Given, OA = 5 cm, O’A = 3cm and OO’ = 4 cm
∴ AO’2 + OO’2 = 32 + 42 = 9 + 16- 25 = OA2
∴ OO’A is a right angled triangle and right angled at O’
Area of ∆OO’A = \(\frac { 1 }{ 2 }\) x O’A x OO’
= \(\frac { 1 }{ 2 }\) x 3x 4= 6sq units …(i)
Also, area of ∆OO’A = \(\frac { 1 }{ 2 }\) x OO’ x AM
= \(\frac { 1 }{ 2 }\) x 4 x AM =2 AM …(ii)
From Eqs. (i) and (ii), we get
2AM = 6 ⇒ AM = 3
Since, when two circles intersect at two points, then their centre lie on the perpendicular bisector of the common chord.
∴ AB = 2 x AM= 2 x 3 = 6 cm
Question 2.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution:
Given: MN and AS are two chords of a circle with centre O, AS and MN intersect at P and MN = AB
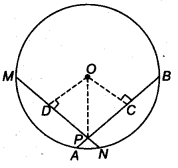
To prove: MP = PB and PN = AP
Construction: Draw OD ⊥ MN and OC ⊥ AB.
Join OP
Proof : ∵ DM = DN = \(\frac { 1 }{ 2 }\) MN (Perpendicular from centre bisects the chord)
and AC = CB = \(\frac { 1 }{ 2 }\) AB (Perpendicular from centre bisects the chord)
MD = BC and DN = AC (∵ MN = AS)…(i)
in ∆ODP and ∆OPC
OD = OC (Equal chords of a circle are equidistant from the centre)
∠ ODP = ∠OCP
OP = OP (Common)
∴ RHS criterion of congruence,
∆ ODP ≅ ∆ OCP
∴ DP = PC (By CPCT)…(ii)
On adding Eqs. (i) and (ii), we get
MD + DP = BC + PC
MP = PB
On subtracting Eq. (ii) from Eq. (i), we get
DN – DP = AC – PC
PN = AP
Hence, MP = PB and PN = AP are proved.
Question 3.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Solution:
Given: RQ and MN are chords of a with centre O. MN and RQ intersect at P and MN = RQ
To prove: ∠ OPC = ∠ OPB
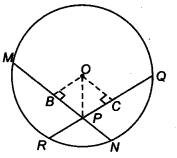
Construction: Draw OC ⊥ RQ and OB ⊥ MN.
Join OP.
Proof: In ∆ OCP and ∆ OBP, we get
∠ OCP = ∠ OBP (Each = 90°)
OP = OP (Common)
OC = OB (Equal chords of a circle are equidistant from the centre)
∴ By RHS criterion of congruence, we get
∆ OCP ≅ ∆ OBP
∴ ∠ OPC = ∠ OPB (By CPCT)
Question 4.
If a line intersects two concentric circles (circles with the same centre) with centre 0 at A, B, C and D, prove that AB = CD (see figure).
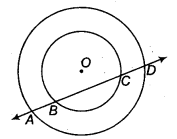
Solution:
Let OP be the perpendicular from O on line l. Since, the perpendicular from the centre of a circle to a chord
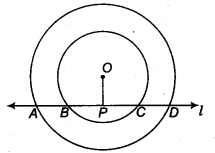
Now, BC is the chord of the smaller circle and OP ⊥ BC.
∴ BP = PC ……(i)
Since, AD is a chord of the larger circle and OP ⊥ AD.
∴ AP = PD …(ii)
On subtracting Eq. (i) from Eq. (ii), we get
AP – BP = PD – PC
⇒ AB = CD
Hence proved.
Question 5.
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Solution:
Let O be the centre of the circle and Reshma, Salma and Mandip are represented by the points Ft, S and M, respectively.
Let RP = xm.
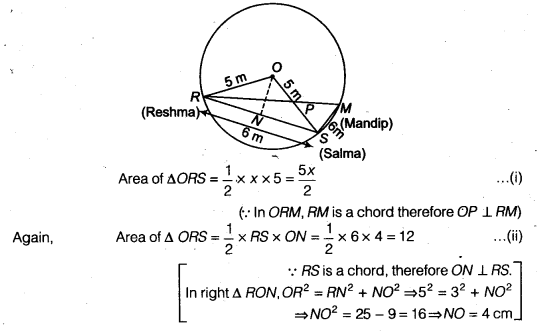
From Eqs. (i) and (ii), we get

Hence, the distance between Reshma and Mandip is 9.6 m.
Question 6.
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Solution:
Let Ankur, Syed and David standing on the point P, Q and R.
Let PQ = QR = PR = x
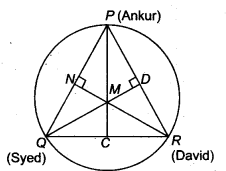
Therefore, ∆ PQR is an equilateral triangle. Drawn altitudes PC, QD and RN from vertices to the sides of a triangle and intersect these altitudes at the centre of a circle M.
As PQR is an equilateral, therefore these altitudes bisects their sides.
In ∆ PQC,
PQ2 = PC2 + QC2 (By Pythagoras theorem)
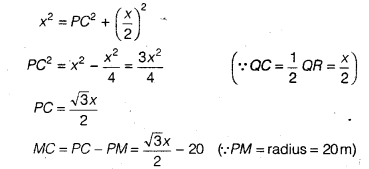
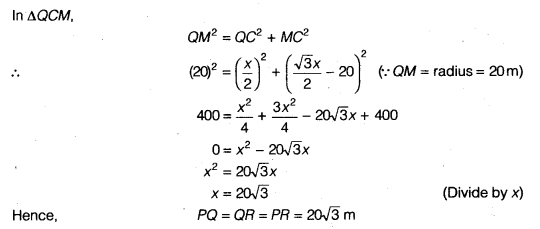
We hope the NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.4, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.4, drop a comment below and we will get back to you at the earliest.